电子耗空对喷焰尘埃等离子体离子波不稳定性的影响

马征征 许正文 徐彬 吴健

(中国电波传播研究所 电波环境特性及模化技术重点实验室,青岛 266107)

电子耗空对喷焰尘埃等离子体离子波不稳定性的影响

马征征 许正文 徐彬 吴健

(中国电波传播研究所 电波环境特性及模化技术重点实验室,青岛 266107)

在离子波不稳定性增长率的计算过程中增加对自洽尘埃电荷数的考虑,以考察电子耗空效应对尘埃等离子体离子波不稳定性增长率的影响. 通过比对多个算例的计算结果发现:随着尘埃数密度的增大,电子耗空的加剧可以导致不稳定性增长率减小;喷焰释放早期的离子波不稳定性增长率可以更低;无论是尘埃数密度还是中性分子数密度单独增大,均可以导致离子波不稳定性增长率的减小. 这表明现有理论方法中隐含的假设不是恒成立.

电子耗空;喷焰;尘埃等离子体;离子波;不稳定性

引 言

20世纪末期以来,空间飞行器在电离层中喷焰造成的雷达回波增强现象引起了科学界的广泛关注和研究[1-10]. 这种现象基本被认为是喷焰产生纳米至微米级的固体尘埃粒子或水汽凝华形成的冰晶尘埃粒子带电后,相对背景电离层等离子体高速运动,激发了等离子体不稳定性,形成不规则体引起的[2]. 针对此问题展开了大致两类方式的理论研究:一类是从等离子体色散关系出发的线性理论研究[1-4];另一类是基于等离子体模拟仿真的非线性理论研究[6-9]. 为检验和改进这些理论,2009年国际上首次开展了以触发等离子体不稳定性为直接目的的火箭喷焰试验,称为带电气溶胶释放试验. 然而,令人疑惑的是试验中所有雷达均未能探测到预期的散射回波增强现象[5].

2011年,Rosenberg等人针对上述试验开展了基于线性理论的个例研究,考虑了离子声波和低混杂波两种离子波不稳定性模式[4]. 首先,在给定了释放参数的前提下,选择尾焰某点处的某一时刻,计算不稳定性增长率. 然后,判断该不稳定性增长率与尘埃流已持续时间之积是否达到阈值,以判定是否足以触发不稳定性. 计算结果表明,试验实际参数并不足以保证不稳定性的成功触发. 进一步地,作者还计算给出了后续试验参数设计建议.

上述理论研究工作首次给出了试验观测结果的一种候选解释.注意到在该现有理论的计算过程中,尘埃电荷数是按照定值给出[4]. 分析可知,当系统中尘埃粒子数密度较低时,自由电子充足,新增加的尘埃粒子只会携带它们而不会影响原有尘埃粒子的带电水平．换句话说,尘埃粒子携带电荷数与尘埃粒子数密度无关. 然而,当尘埃数密度较大时,尘埃对电子的吸附效应将造成电子密度在背景水平上的显著降低,即电子耗空(吞噬)效应. 电子耗空将反过来限制尘埃粒子能够携带到的平衡电荷数,导致尘埃粒子携带电荷数与尘埃粒子数密度相关. 事实上对于喷焰释放早期的稠密尘埃团,电子耗空效应非常显著. 因此,根据上述分析,尘埃电荷数不可按定值给出,针对电子耗空场景,由于尘埃数密度、电子密度和尘埃电荷数同步发生变化,给不稳定性增长率带来的总体影响倾向并不明确.

现有理论中为保证不稳定性触发判定方法不至于产生过高估计,隐含了整个尘埃流持续时间内的不稳定性增长率均达到所选时刻的不稳定性增长率的假设. 然而,对于喷焰释放早期,除了上述电子耗空效应,伴随稠密尘埃团的稠密中性气体分子团也可以通过更强烈的碰撞作用抑制不稳定性的增长. 这些效应可能导致假设不满足.

本文将在离子波不稳定性增长率计算过程中增加对自洽尘埃电荷数的考虑,以研究电子耗空效应对离子声波不稳定性增长率的影响. 并考察现有理论中整个尘埃流持续时间内的不稳定性增长率均达到所选时刻的不稳定性增长率的假设是否成立.

1 计算方法

针对喷焰释放早期的电子耗空场景,必须考虑自洽的尘埃电荷数. 以下先建立电子耗空效应下自洽尘埃电荷数的求解方法,再进一步求解离子波不稳定性增长率.

1.1 电子耗空效应下的自洽尘埃电荷数

电离层中的尘埃粒子将通过碰撞作用吸附电子和离子而携带电荷. 由于电子的热运动速度远大于离子,尘埃粒子更容易吸附电子而携带负电荷并具有负电势. 针对高速运动的尘埃粒子,还必须考虑尘埃粒子的尾流效应. 给出负电势下的尘埃粒子充电方程[11]:

(1)

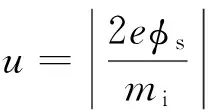
尘埃粒子的吸附作用将改变电子密度,所有带电物质组分满足电中性方程:

ni=ne+ndZd.

(2)

联立式(1)和式(2),即可解出尘埃粒子表面电势. 再由球体电势公式

(3)

即可得到尘埃粒子平衡电荷数. 注意到尘埃粒子达到平衡电荷数需要较短的时间,参考现有理论,忽略该效应[4].

1.2 离子波不稳定性的增长率

依据现有理论[4,12],建立三维直角坐标系x-y-z,磁场指向z方向,等离子体中的色散关系方程为

1+χe+χi+χd=0,

(4)

(5)

式中:k为波数,限制在y-z平面内;λD为德拜长度;v为热速度,ν为碰撞频率; 下标e、i和d分别代表电子、离子和尘埃粒子;be=(kyρe)2,ρe为电子回旋半径;Γ0(be)=I0(be)exp(-be),I0是零阶修正Bessel函数;Z为等离子体色散函数,其参数为

(6)

ω为复谐振频率,其虚部γ=Im(ω)即为不稳定性增长率.

当尘埃流速度垂直于磁场而沿y方向时,式(4)和式(5)可用于求解低混杂波不稳定性. 当尘埃流速度平行于磁场时,可用于求解离子声波不稳定性.

2 参考例

参考Rosenberg等人开展的三个个例研究工作[4],选择其中第一个例子作为本文的参考例. 其给定的部分尘埃参数和环境参数如表1所示.

表1 参考例中的部分尘埃参数和环境参数取值

原例中设定尘埃粒子平衡电荷数为恒定值15[4]. 采用本文§1.1所述方法重新计算得到尘埃粒子平衡电荷数的平均值为13.80. 此外,还有一些本文不涉及或不关注的参数均直接依照原例取值. 进一步使用本文§1.2所述方法计算得到离子声波和低混杂波不稳定性增长率随波数的二维分布,如图1和图2所示.

图1 离子声波不稳定性增长率γ随波数的二维分布

图2 低混杂波不稳定性增长率γ随波数的二维分布

计算表明,离子声波和低混杂波不稳定性增长率最大值为16.5 s-1.

3 尘埃数密度对不稳定性增长率的 影响

在参考例的基础上,计算尘埃数密度取值为2、4、8、16倍的情况. 定义电子耗空度为由尘埃粒子吸附造成电子密度下降的百分比幅度,即ndZd/ni×100%. 为突出研究重点,只针对离子声波不稳定性开展研究,并将所有计算结果汇总于表2.

表2表明: 当尘埃数密度增大时,尘埃平衡电荷数逐渐降低,两者共同作用下,电子耗空度逐渐增大.而离子声波不稳定性增长率并未随尘埃数密度增大而单调变化,其表现为先升高再降低; 当尘埃数密度提升至16倍时,离子声波不稳定性增长率反而较参考例更低. 在本组计算例中,不稳定性增长率最大值(23.7 s-1)的出现对应的电子耗空度为95.1%.

表2 电子耗空对离子声波不稳定性增长率的影响

因此,随着尘埃数密度的增大,电子耗空度的加剧可以导致不稳定性增长率减小. 很明显,该规律具有普适性,适用于不限于喷焰释放早期在内的所有电子耗空场景.

4 喷焰释放早期的计算和分析

考虑喷焰释放更早期的场景,取尘埃数密度和中性分子数密度为参考例的2倍. 类似地,计算得到尘埃粒子平衡电荷数的平均值为7.55. 离子声波和低混杂波不稳定性增长率随波数的二维分布如图3和图4所示.

图3 离子声波不稳定性增长率γ随波数的二维分布

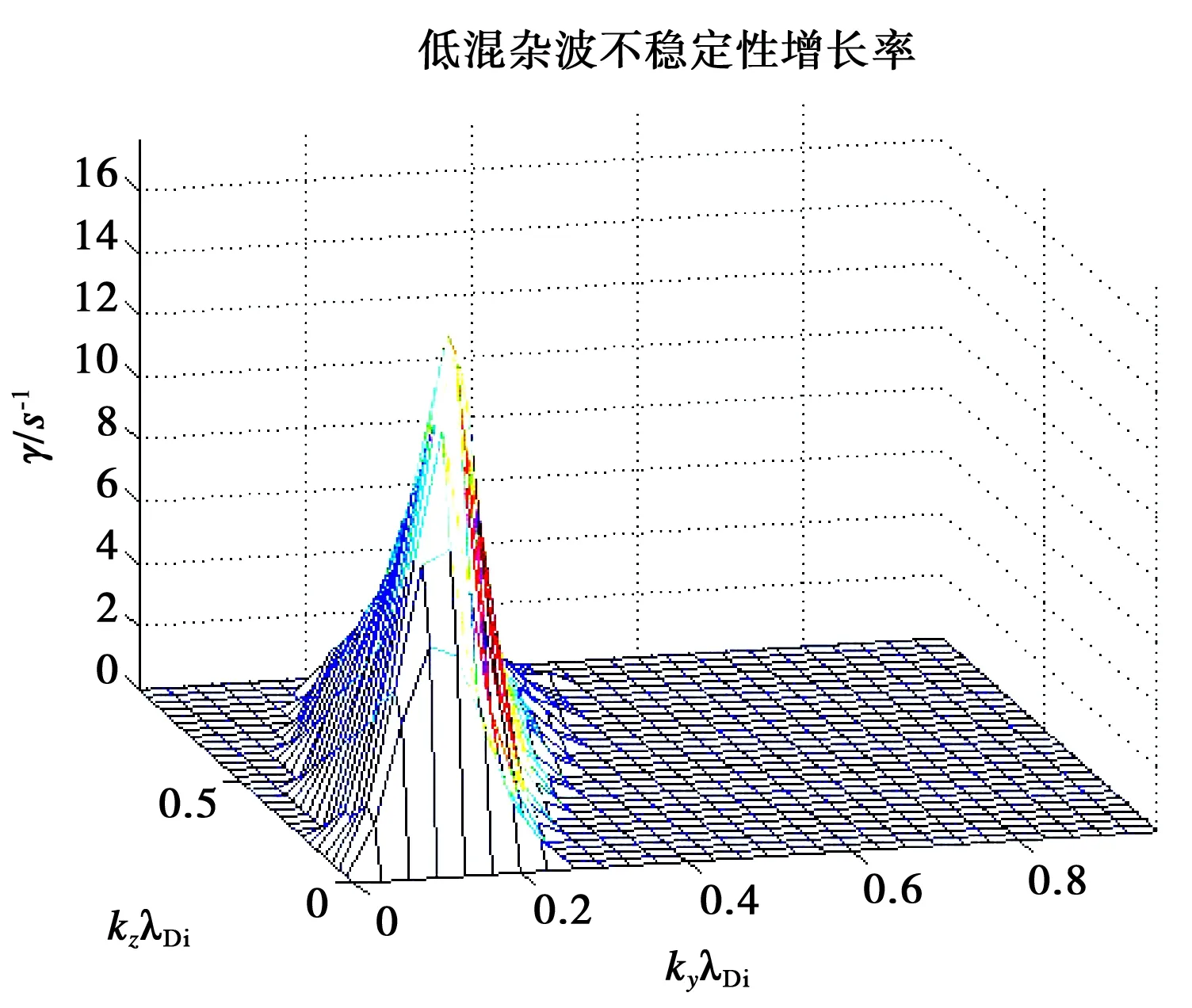
图4 低混杂波不稳定性增长率γ随波数的二维分布

计算表明,离子声波和低混杂波不稳定性增长率最大值为15.9 s-1.

通过该例和参考例计算结果的对比看到,对于喷焰释放早期尘埃数密度和中性分子数密度更高的情形,不稳定性增长率可以更低. 这表明: 整个尘埃流持续时间内的不稳定性增长率均达到所选时刻的不稳定性增长率的假设不成立.

进一步地,下面我们分别考察尘埃数密度和稠密中性气体分子团对不稳定性增长率的影响. 为突出研究重点,只针对离子声波不稳定性开展研究.

首先,考虑尘埃数密度取值为参考例的2倍,中性分子数密度取值与参考例一致. 计算得到尘埃粒子平衡电荷数的平均值为7.55. 给出离子声波不稳定性增长率随波数的二维分布,如图5所示.

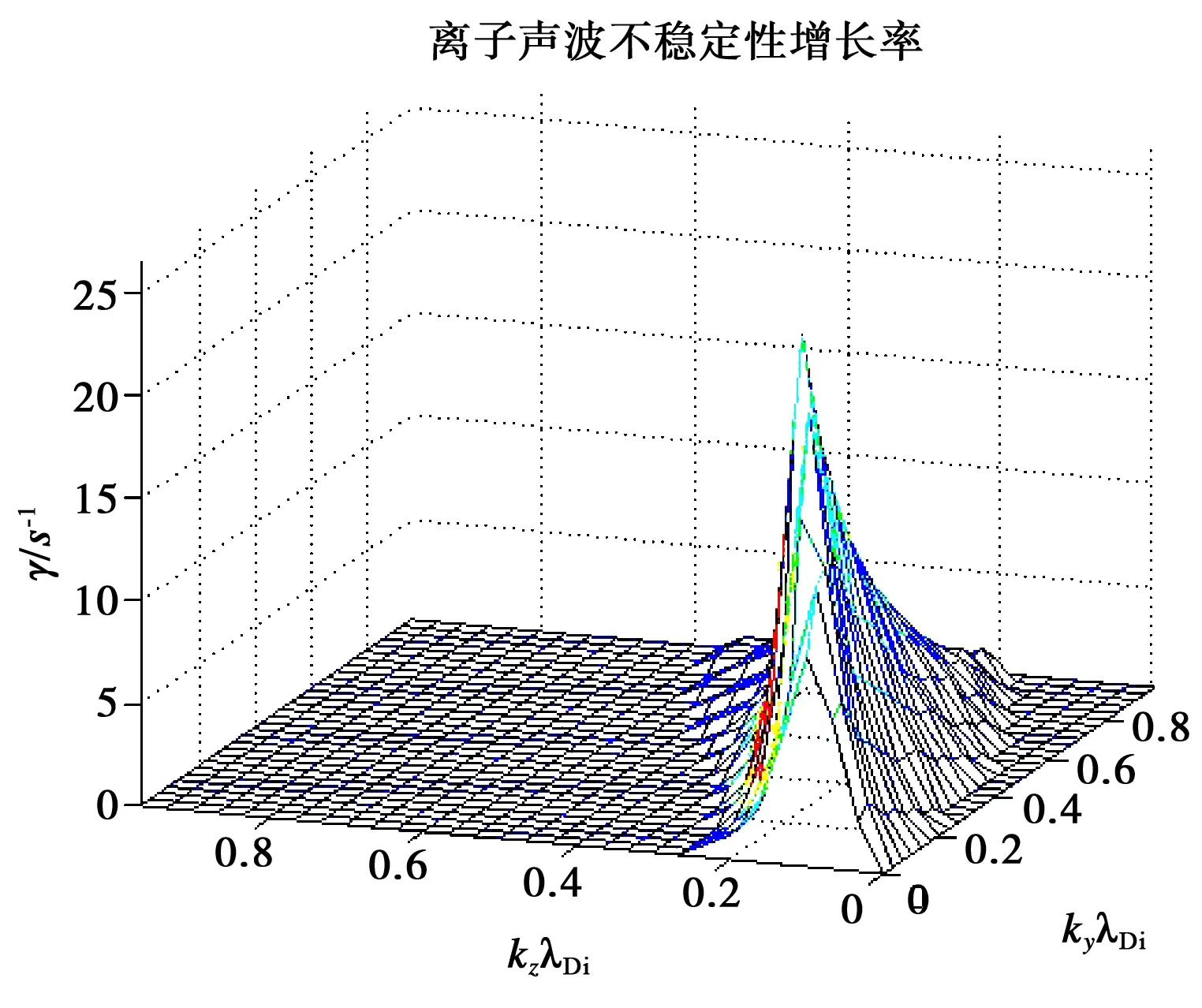
图5 离子声波不稳定性增长率γ随波数的二维分布

计算表明,离子声波不稳定性增长率最大值为23.7 s-1.

然后,考虑中性分子数密度取值为参考例的2倍,尘埃数密度取值与参考例一致. 计算得到尘埃粒子平衡电荷数的平均值为13.80. 给出离子声波不稳定性增长率随波数的二维分布,如图6所示.

图6 离子声波不稳定性增长率γ随波数的二维分布

计算表明,离子声波不稳定性增长率最大值为12.6 s-1.

将上述各计算例结果汇总于表3. 通过比较发现,在该组计算例中,尘埃数密度单独增大引起不稳定性增长率提升,中性分子数密度单独增大引起不稳定性增长率降低. 本计算例中喷焰释放早期不稳定性增长率降低是由中性分子数密度增大造成.

表3 尘埃数密度和中性分子数密度对

分析可知,中性分子数密度增大将导致碰撞频率提升,抑制不稳定性的增长.因此,不稳定性增长率应随中性分子数密度增大而单调减小.而对于尘埃数密度,虽然本组计算例中尘埃数密度增大引起不稳定性增长率提升,但由第3节的结论可知,在更宽泛的范围内尘埃数密度增大可能引起不稳定性增长率减小.

综上所述,无论是尘埃数密度单独增大还是中性分子数密度单独增大,均可以导致离子波不稳定性增长率的减小,导致喷焰释放更早期的不稳定性增长率更低. 这进一步强化了如下结论: 现有理论方法中隐含的整个尘埃流持续时间内的不稳定性增长率均达到所选时刻的不稳定性增长率的假设不是恒成立.

5 结 论

本文通过建立考虑电子耗空效应的离子波不稳定性增长率计算方法,计算了多个计算例下的不稳定性增长率,通过比对和分析,得到如下两个主要结论:

1) 离子声波不稳定性增长率并未随尘埃数密度增大而单调变化,其表现为先升高再降低. 因此表明,随着尘埃数密度的增大,电子耗空度的加剧可以导致不稳定性增长率减小. 该规律具有普适性,适用于不限于喷焰释放早期在内的所有电子耗空场景.

2) 对于喷焰释放早期尘埃数密度和中性分子数密度更高的情形,离子波不稳定性增长率可以更低. 进一步研究发现,无论是尘埃数密度单独增大还是中性分子数密度单独增大,均可以导致离子波不稳定性增长率的减小. 这表明: 现有理论方法中隐含的整个尘埃流持续时间内的不稳定性增长率均达到所选时刻的不稳定性增长率的假设不是恒成立. 因此应对现有理论方法提供修正.

当然,鉴于尘埃等离子体理论的复杂性,计算具体过程中仍包含了一些近似和假设,还有待于继续考察和完善.

[1] BERNHARDT P A, GANGULI G, KELLEY M C, et al. Enhanced radar backscatter from space shuttle exhaust in the ionosphere[J]. Journal of geophysical research, 1995, 100(A12): 23811-23818.

[2] ROSENBERG M, SALIMULLAH M, BHARUTHRAM R. Lower hybrid instability driven by charged dust beam[J]. Planetary and space science, 1999, 47: 1517-1519.

[3] ROSENBERG M, SORASIO G. Lower hybrid instability in ionospheric gas-dust formations from rocket exhaust[J]. Journal of spacecraft and rockets, 2006, 43(1): 245-248.

[4] ROSENBERG M, BERNHARDT P A, CLARK S E. Excitation of ion waves by charged dust beams in ionospheric aerosol release experiments[J]. Planetary and space science, 2011, 59(4): 312-318.

[5] BERNHARDT P A, BALLENTHIN J O, BAUMGARDNER J L, et al. Ground and space-based measurement of rocket engine burns in the ionosphere[J]. IEEE transactions on plasma science, 2012, 40(5): 1267-1286.

[6] SCALES W A, BORDIKAR M R, MAHMOUDIAN A, et al. Irregularities associated with creation of dusty plasmas in the near-Earth space environment[J]. IEEE transactions on plasma science, 2010, 38(4): 880-885.

[7] FU H, SCALES W A. Nonlinear evolution of the ion acoustic instability in artificially created dusty space plasmas[J]. Journal of geophysical research, 2011, 116(A10): 1223-1228.

[8] FU H, SCALES W A. Nonlinear evolution of the lower hybrid irregularities in artificially created dusty space plasmas[J]. Journal of geophysical research, 2012, 117(A07): 594-602.

[9] 马征征, 徐彬, 许正文. 尘埃等离子体混合模型中电荷-电势问题的迭代法求解[J]. 电波科学学报,2015, 30(3): 549-553.

MA Z Z, XU B, XU Z W. Solving charge-potential issue in dusty plasma hybrid model by iteration method[J]. Chinese journal of radio science, 2015, 30(3): 549-553. (in Chinese)

[10]石雁祥, 葛德彪, 吴健. 环境压强对固体火箭喷焰电导率的影响[J]. 电波科学学报, 2008, 23(6): 1115-1118.

SHI Y X, GE D B, WU J. Influence of pressure of environment on conductivity of solid rocket exhaust plume[J]. Chinese journal of radio science, 2008, 23(6): 1115-1118. (in Chinese)

[11]WHIPPLE E C. Potentials of surfaces in space[J]. Reports on progress in physics, 1981, 44(11): 1197-1250.

[12]SHUKLA P K, MAMUN A A. Introduction to dusty plasma physics[M]. IOP Publishing Ltd, 2002.

徐彬 (1982-),男,辽宁人,中国电波传播研究所高级工程师,博士,主要研究方向为电离层探测与理论等.

The influence of electron depletion to exhaust dusty plasma ion wave instability

MA Zhengzheng XU Zhengwen XU Bin WU Jian

(NationalKeyLaboratoryofElectromagneticEnvironment,ChinaResearchInstituteofRadiowavePropagation,Qingdao266107,China)

We considered the self-consistent dust charge number in calculating ion wave instability growth rate, in order to survey the influence of electron depletion effect to dusty plasma ion wave instability growth rate. By comparing calculation results of several cases, we found that as the dust number density increases, electron depletion intensification could lead to the decrease of instability growth rate, and that the ion wave instability growth rate could be lower on the early stage of the released exhaust. The number density increase of either dust or neutral molecule can lead to the decrease of ion wave instability growth rate. This indicates that the assumption in present theory is not always correct.

electron depletion; exhaust; dusty plasma; ion wave; instability

10.13443/j.cjors.2016112901

2016-11-29

国家自然科学基金(No. 11672068；41104102；61601419)

P354

A

1005-0388(2016)06-1087-06

马征征 (1982-),男,湖北人,中国电波传播研究所高级工程师,博士,硕士生导师,主要研究方向为中高层大气、电离层探测与理论等.

许正文 (1971-),男,安徽人,中国电波传播研究所研究员,博士,主要研究方向为电波传播.

马征征, 许正文, 徐彬, 等. 电子耗空对喷焰尘埃等离子体离子波不稳定性的影响[J]. 电波科学学报,2016,31(6):1087-1092.

MA Z Z, XU Z W, XU B, et al. The influence of electron depletion to exhaust dusty plasma ion wave instability[J]. Chinese journal of radio science,2016,31(6):1087-1092.(in Chinese). DOI: 10.13443/j.cjors.2016112901

联系人： 马征征 E-mail: zh.zh.ma.7@gmail.com

DOI 10.13443/j.cjors.2016112901