有限单演半群的性质
2016-03-06徐文锋
徐文锋
(韶关学院数学与统计学院,广东韶关512005)
有限单演半群的性质
徐文锋
(韶关学院数学与统计学院,广东韶关512005)
单演半群可由一个元素生成.通过对一类给定的有限单演矩阵半群进行研究,分类讨论有限单演半群的格林关系,得到了一些有限单演半群的性质.
单演半群;矩阵半群;有限单演矩阵半群
半个世纪以来,半群理论得到了很好的发展.如同循环群在群论中的地位,单演半群在半群理论中也起到了很重要的作用.矩阵在理论和实际中都有很重要的意义,是一个非常重要的工具,将矩阵与半群理论相结合得到矩阵半群.矩阵半群也可以看成是半群表示理论的发展.近些年来,国内外有不少相关问题的研究,如完全单的矩阵半群,正则矩阵半群,Clifford矩阵半群等研究[1-3].
单演半群由于其生成元仅有一个元素,结构十分简单.本文在文献[4]的基础上,利用已经给出的一类有限单演矩阵半群,进行进一步的研究,得到了这类矩阵半群的格林关系以及一些新的性质.再将这些关系和性质推广到一般的有限单演半群.
本文分三部分完成.第一部分,介绍了单演半群和矩阵半群的概念和一些已知的性质.在第二部分给出了文献[4]中的一类单演矩阵半群的例子.在第三部分中,分类讨论了这类单演矩阵半群的格林关系和性质,并将这些性质推广到一般的有限单演半群上.
1 预备知识
本文所用到的半群代数理论的基本概念及符号,如半群、格林关系等,均与文献[5]相同,本文将直接引用而不再一一定义.
定义1S是一个半群,如果存在S中的一个元素a,使得S={a,a2,a3,…},称半群S是单演半群,记S=.如果序列a,a2,a3,…中不出现重复,也就是说am=an⇒m=n,则称S=是一个无限单演半群.如果序列a,a2,a3,…中出现重复,即存在正整数m,r使得am=am+r成立,则称S=是一个有限单演半群,并且把满足条件的最小元m和r分别称为有限单演半群S的指数和周期.
定义2(Mn(F)·)表示数域F上全体n阶方阵按照通常运算构成的半群,如果S是(Mn(F)·)的子半群,则称S为一个矩阵半群.
定义3设S是一个矩阵半群,如果存在S中的一个矩阵A使得S={A,A2,A3,…},称半群S是单演矩阵半群.
定义4如果一个矩阵半群中每个矩阵的秩都相等,则称它为等秩矩阵半群.此时可用其中任意一个矩阵的秩表示矩阵半群的秩.
本文主要讨论有限单演矩阵半群的性质,下面给出文中需要用到的一些已知结论.
引理1S=是一个指数为m周期为的r有限单演半群,则下面结论成立[5]:
(1)am=am+r;
(3)ka={am,am+1,…am+r-1}是的一个循环子群;
(4)对任意的u,v∈N,am+n=am+v当且仅当u=v(modr).
引理2两个有限单演半群同构的充分必要条件是它们有对应相等的指数和周期[5].
引理3矩阵半群的每一个关系T=L,R,D,H,J类都是单秩的[25].
2 一个例子
引理4设m,r是任意给出的两个正整数,若r=1,令Jm为m阶的幂等若当块,即:
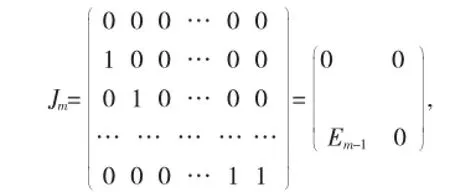
那么由Jm生成的半群是指数为m周期为1的有限单演半群S=<Jm>;
若m=1,令Ir是主对角线上的元素全为r次单位且至少有一个本原根的对角矩阵,那么由Ir生成的半群是指数为1周期为r的有限单演半群S=<Ir>;
3 主要结论
在引理4中,对于任意一个正整数对(m,r),都给出了一个具体的以m为指数r为周期的有限单演矩阵半群.下面通过对这一类矩阵半群的研究,给出一些有限单演半群的性质.
性质1设S=<a>是一个指数为m,周期为1的有限单演知半群,则S一定有零元.
证由引理4(1),利用矩阵的乘法运算法则,得到Jmm=0,故半群S=<Jm>包含零矩阵.再由引理2,知任意一个以m为指数,1为周期的有限单演半群S=包含零元.
性质2设S=是一个以m为指数r为周期的有限单演半群,若S含有零元,则周期r=1.
性质3设S=是一个指数为1,周期为r的有限单演知半群,则S是循环群.
证由引理4(2)知S=<Ir>是一个循环矩阵群.再由引理2,得出任意一个以1为指数,r为周期的有限单演半群S=都是循环群.
性质4设S=是一个有限单演半群,若S含有单位元,则指数m=1,S=是循环群.
证已知S=是一个有限单演半群,则有指数m,周期r.由引理4,存在一个指数m,周期r的单演矩阵半群U与之同构.由于S含有单位元,所以U也一定含有单位元.再由引理4知,当且仅当m=1时,单演矩阵半群S=<Ir>包含单位矩阵.所以S含有单位元,则m=1.矩阵半群S=<Ir>是循环矩阵群,故S=是循环群.
性质5设S=<Ir>是引理4(2)给出的以1为指数r为周期的有限单演矩阵,则S=<Ir>是等秩矩阵群.
证由引理4(2),显然有矩阵Ir的秩等于r.根据矩阵的乘法运算法则,得Irr=E,所以矩阵Irr的秩等于r.由矩阵秩的性质有r(Ir)=r(I2r)=…=r(Irr)=r.故S=<Ir>是等秩矩阵群,并且矩阵群S=<Ir>的秩等于r.
下面根据引理4和性质5来分类讨论有限单演半群的格林关系.
定理1设S=是一个有限单演半群,m为半群S的指数,r为S的周期,则有以下结论:
(1)若r=1,则S={a,a2,…am},则S中每一个D类仅有一个元素.
(2)若m=1,则S={a,a2,…ar},则S仅有一个H类,即所有元素都在同一个H类中.
(3)若m>1且n>1,则S={a,a2,…am+r-1},则当1≤i≤m时,每一个ai属于不同的D类中,当i≥m时,每一个ai属于同一个D类,并且是同一个H类.
证(1)当m>1且r=1,则S=={a,a2,…am}.由引理4,有同构的单演矩阵半群显然有矩阵Jm的秩为m-1,并且有r(Iim)=m-i,其中1≤i≤m.由引理4知每个D类都是单秩的,所以每一个元素J属于不同的D类.因此,若r=1,则半群S={a,a2,…am}中每一个D类仅有一个元素.
(2)当r>1且m>1,则S=={a,a2,…ar}.由性质5知I=<Ir>是等秩矩阵群.所以I仅有一个H类.所以S=={a,a2,…ar}所有元素都在同一个H类.
(3)当m>1且r>1,则S=={a,a2,…am+r-1}.由引理4,有同构的单演矩阵半群1>.显然有矩阵的秩为=m+r-1,其中1≤i≤m.当i≥m时,=r.因此,当1≤i≤m时,每一个ai属于不同的D类,当i≥m时,每一个ai属于同一个D类,并且是同一个H类.
定理2设S=为一个有限单演半群,如果指数m>1,则半群S的生成元唯一.
证从引理4中的矩阵半群出发,给出定理的证明.
当m>1且r=1,则S=={a,a2,…am}.由引理4有同构的单演矩阵半群显然有矩阵Jm的秩等于m-1,任意矩阵的秩都小于m-1,所以有矩阵的秩小于m-1,其中k为任意正整数,1≤i≤m.因此Jm∉<>,其中(1<i≤m-1).
所以有限单演半群S=,如果指数m>1,则半群S的生成元唯一.
推论1设S=为一个有限单演半群,如果指数m>1,对任意ai∈S且ai≠a,则<ai>是S的一个真子半群.
[1]朱用文.完全单的矩阵半群[J].数学进展,2007,36(1):76-80.
[2]朱用文.正则矩阵半群[J].数学进展,2009,38(1):75-78.
[3]陈大亮,朱用文.Clifford矩阵半群[J].烟台大学学报(自然科学和工程版),2010,23(4):251-255.
[4]乔占科.循环半群的矩阵表示[J].河西学院学报:2002(5):10-13.
[5]John M H.Fundamentals of Semigroup Theory[M].Oxford:Oxford University Press,1995.
[6]赵雨清.单演半群的几条性质[J].湘潭师范学院学报(自然科学版),2004,26(1):20-29.
Some Properties of Monogenic Semigroups
XU Wen-feng
(School of Mathematics and Statistics,Shaoguan University,Shaoguan 512005,Guangdong,China)
A monogenic semigroup can be generated by a singleton element.Useing a special kind of finite monogenic semigroup of matrices,it discusses their Green's ralations and obtain some new properties of finite monogenic semigroup.
monogenic semigroup;matrix semigroup;finite monogenic matrix semigroup
O152.7
A
1007-5348(2016)12-0004-03
(责任编辑:邵晓军)
2016-11-08
徐文锋(1983-),女,江西都昌人,韶关学院数学与统计学院讲师,硕士;研究方向:半群代数.
