酉空间两类标准正交基的同步构造方法
2016-03-06刘玲
刘玲
(韶关学院数学与统计学院,广东韶关512005)
酉空间两类标准正交基的同步构造方法
刘玲
(韶关学院数学与统计学院,广东韶关512005)
利用矩阵奇异值分解技术给出两个酉空间特殊标准正交基的同步构造方法.
奇异值分解;酉空间;标准正交基
标准正交基是酉空间[1]的重要概念之一,选取简单的标准正交基对于简化研究过程、降低推导难度有着重要的意义.在研究子空间、正交投影以及广义逆[2]的扰动规律时,往往还需要对多个酉空间同时进行讨论,怎样对多个酉空间进行同步的酉变换,从而找出简单的标准正交基,是一个非常有意义的问题.
本文利用矩阵奇异值分解技术,给出同步寻找两个酉空间特殊标准正交基的酉变换方法,结果表明:可以使用矩阵奇异值信息构造出形式较为简单的标准正交基.
在后续讨论中,用AT表示矩阵A的转置,AH表示矩阵A的共轭转置,diag(x)表示以向量x的分量为对角元的对角矩阵,Im表示m阶单位矩阵,rank(A)表示A的秩.
1 预备知识
先回顾矩阵奇异值分理论的相关概念和结果.
定义1[3]设A∈Cn×n.AHA的特征值的非负平方根称为A的奇异值;A的奇异值的全体记为σ(A).
引理1[3](奇异值分解定理)设A∈Cm×n,且rank(A)=r,则存在酉矩阵U∈Cm×m,V∈Cn×n,使得:

其中Σr=diag(σ1,…,σr),σ1≥…≥σr>0.
2 主要定理及证明
定理设L和V是Cn中两个k维子空间,1≤k≤n,则存在酉变换U,使得:
(1)当2k≤n时,(Ik0)T和(C D 0)T分别为UL和UV的标准正交基,其中:
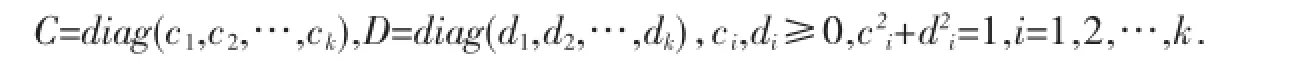
证先证明(1).
分别取L和V的两个标准正交基A1=(α1,α2,…,αk),B1=(β1,β2,…,βk).由基扩张定理,存在A2=(αk+1,αk+2,…, αn),B2=(βk+1,βk+2,…,βn),使得:

是Cn的标准正交基.令:

显然M也是酉矩阵,由奇异值分解定理,存在酉矩阵Q11和R11,使得QH11M11R11=C,其中C=diag(c1,c2,…, ck),0≤c1≤c2≤…≤c2<cs+1=…=ck=1.

这表明M21R11的前s列是相互正交的,将其单位化并扩充为Cn-k中的标准正交基后可得酉矩阵Q^22,此时有:
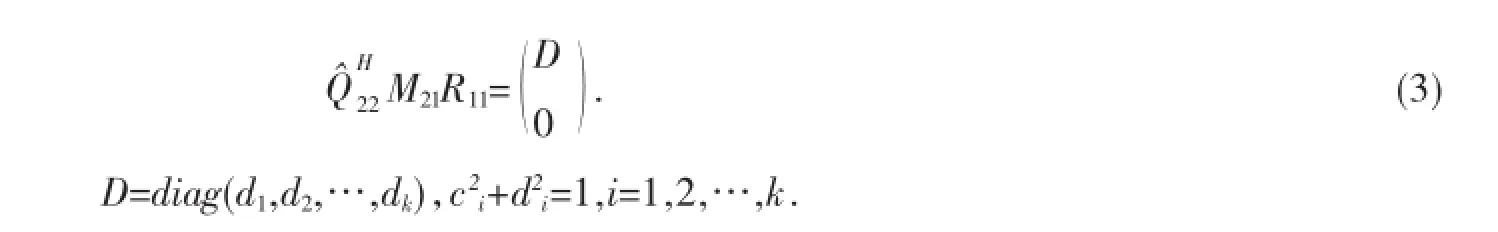
类似地,存在酉矩阵R22,使得:
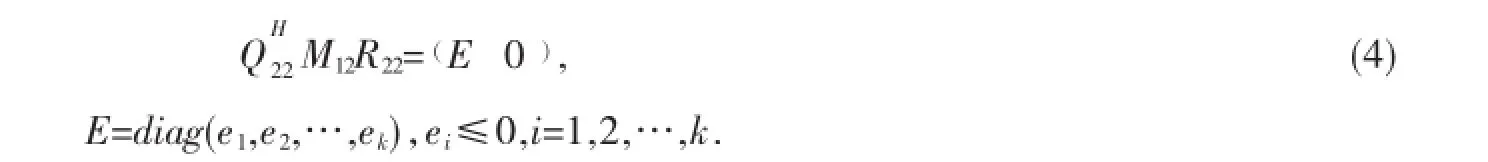
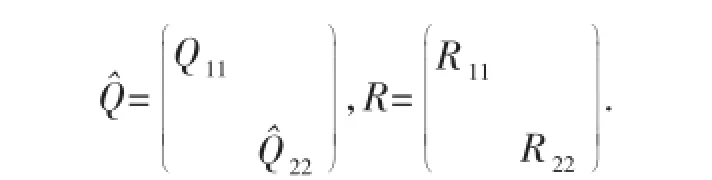
结合(1)~(4)式可得:
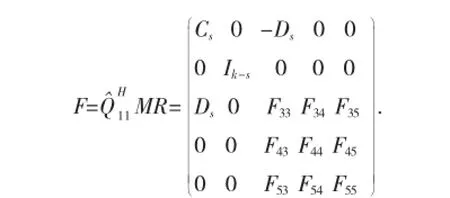
其中Ds=diag(d1,d2,…,ds).显然F是酉矩阵,因此有F33=Cs,而F34、F35、F43、F53都是零矩阵.记:
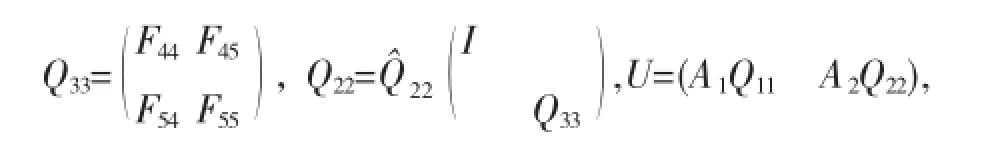
综上易得:
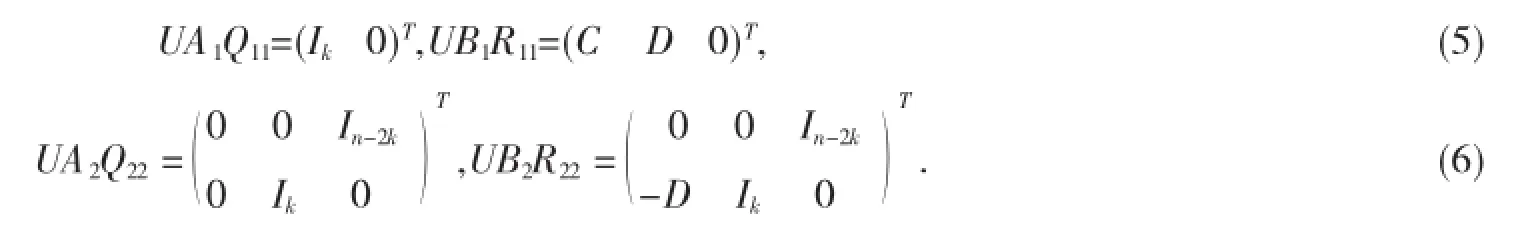
(5)式表明,(Ik0)T和(CD0)T分别为UL和UV的标准正交基.
对于(2)式,注意到2k≤n等价于2(n-k)≥n,把k替换为n-k,则(6)式给出了2k≥n时UL和UV的标准正交基:
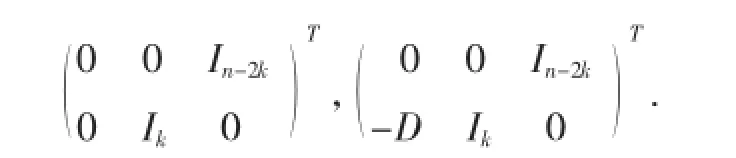
将它们前n-k行变号,并通过适当的置换后仍然是标准正交基,即结论(2)是成立的.证毕.
3 结语
定理1的几何意义是对于任意给定的两个维数相同的酉空间,可以对它们同时进行相同的酉变换U,从而找到(5)式和(6)式所示的简单标准正交基.同时,U的构造方式以及最终标准正交基的计算公式从定理1的证明过程中都可以得到.
[1]孙继广.矩阵扰动分析[M].北京:科学出版社,2001.
[2]Golub G H,Van Loan C F.Matrix Computations[M].London:The Johns Hopkins University Press,1989.
[3]徐树方.矩阵计算的理论与方法[M].北京:北京大学出版社,1995.
Synchronous Construction Method for the Two Types of Normal Orthogonal Basis in Unitary Space
LIU Ling
(School of Mathematics and Statistics,Shaoguan University,Shaoguan 512005,Guangdong,China)
The synchronous construction method for the special normal orthogonal basis of two unitary spaces is given by the technique of singular value decomposition.
singular value decomposition;unitary space;normal orthogonal basis
O151.21
A
1007-5348(2016)12-0001-03
(责任编辑:邵晓军)
2016-10-07
刘玲(1981-),女,湖南永州人,韶关学院数学与统计学院讲师,硕士;研究方向:应用数学.
