0—1背包模型在小餐馆客户关系协调中应用

2016-03-04张笑一

电脑知识与技术 2015年36期

张笑一

摘要：为解决顾客因上菜慢造成小饭馆回头客流失现象，设计合理餐饮管理流程；利用0-1背包模型特例建立问题解决模型；visual studio 2010下用C语言编写能输出合理做菜顺序的管理程序；这些输出数据可缓解客户关系并辅助管理者决策。

关键词：协调客户关系；0-1背包问题特例；信息管理系统；小餐馆；程序设计

中图分类号：TP311 文献标识码：A 文章编号：1009-3044（2015）36-0101-03

Abstract： Design rational order control process， to solve little old consumer problem cause they have waited for food； Construct problem model using 0-1 knapsack model special example； Coding C program under the visual studio 2010 to output rational cook order； The data can reduce

unhappy feeling in the consumer group and help manager to make better choice.

Key words： deal with trading relationship； 0-1 knapsack problem special example； information manage system； small restaurant； program design

1 概述

0-1背包问题是遗传算法中的经典问题。背包问题是由MERKLE和HELLMAN[2]提出的。一直是算法研究的热点之一。许多问题都可以归类为背包问题，如资源分配、投资解决、装载设计、Web服务组合问题等[3]。近年来，用遗传算法求解背包问题的研究相当活跃，遗传算法[4]具有简单通用，全局寻优能力强，较强的鲁棒性等优点在求解背包问题上已经显示了巨大的优势[1]。遗传算法的基本流程是在设置初始种群后，经过选择、交叉、变异操作后得到新种群。如此循环后，在满足终止条件的那次循环停止并输出我们要观察的最终数据。

处理背包问题可以把不同搜索算法和遗传算法的技术融合组成混合遗传算法。贪婪算法是求解背包问题的经典算法，是指采用逐步构造最优解的方法，在每个阶段，都根据贪婪准则看出一个看上去最优的策略[5]。关于背包问题的解决，文献[6]提出了关于贪婪算法的混合遗传算法。文献[7]提出改进的排挤遗传算法来解决背包问题（运用惩罚函数和贪婪算法）。文献[8]在贪心和解码算法的融合后，设计了基于文明群体的混合遗传算法解决背包问题。文献[9]将贪心算法和经典遗传算法相融合，提出了一种新的混合遗传算法。该方法提高了解的收敛速度并一定程度克服了出现局部最优解的情况发生。文献[10]结合了遗传和贪婪算法，利用佳点集产生新的交叉算子，优化了子代选择的方法。

2 问题提出

小细节的不足造成顾客反感的例子有很多。长时间等待上菜，顾客会对小饭店产生很坏的印象，这造成回头客减少，是值得关注并解决的问题。本文目的是在建立合理的上菜规则下，抽象出合理的数学模型并用编程语言做出程序来帮助老板做决策。

3 方案设计与模型建立

如果饭馆老板可以在客人普遍能接受的时间内让每桌客人至少能吃到一道菜，就能解决上菜时间不满意的问题。

基于以上思考，本文总结了上菜管理及实施规则：（3.1）根据生活经验得出客人最大忍耐时间；（3.2）规范后厨管理制度：打烊前保证切菜工把原料备好并规定每道菜最合理烹制时间；（3.3）通知厨师炒菜前，总要核对每桌未上菜品和制作时间并计算最大忍耐时间内确保最多桌子能增加一道菜的最优上菜策略；（3.4）通知后厨做菜并安抚此轮不能增加菜品的顾客；（3.5）厨师烹饪期间，新食客进来要提前通知该轮无法点菜；（3.6）若此轮都烹饪结束后仍有业务，从（3.3）开始按顺序执行；（3.7）（3.6）中执行（3.3）后应检查是否存在此规则下两轮无法吃到第一道菜的顾客，可及时通知其离开，以此确保顾客不会浪费时间。

由于上菜规则涉及繁杂的加减运算，因此有必要建立信息系统帮助管理者做决策。从需求看，应首先建立（3.3）的数学模型。第二步用程序实现计算过程并输入数据得到有效的决策数据。

0-1背包的模型： max∑kixi （3.8）， s.t ∑uixi≤c。（3.9），其中i=1…n；∑表示i指标在1～n遍历相加的值；c为常量，做不等式上界；xi∈{0，1}（在0和1两个值之间选择其一取值）。

0/1背包问题的简单描述：设有1个背包，n个物品。每个物品含有一定的重量和价格，第j个物品的重量为Wj，价格为Pj。要求从n个物品中取出若干物品，使重量和不超过界值wl的情况下价格达到最大。[1]（j=1….n）

从以上模型和描述解释可以看出，若令每个ki均为1，ui代表厨师炒某道菜时间，c代表10，那么（3.8）式可以表示十分钟内饭桌上菜的最大桌数（3.9）式表示可以一次性决定做的菜，并且这些菜必须不能超过10分钟做完。这恰好说明该要建立的模型是0-1背包问题的特殊取值后的情形。

对背包问题的求解可用很多搜索优化的算法。根据具体关注的问题，不采用搜索优化方法，而采用普通的面向结构程序设计方法。原因在于：1）我们要解决与整数相关的简单问题模型；2）表示每张桌子是否做菜、由xi组成的向量有2的n次幂种可能值，并且每个策略向量每个位置取0值或1值的分布并无规律，这就使得我们在程序中保存某策略耗时值时不能用for循环语句，小餐馆规模小方便逐次把计算结果录入定义好的变量中；3）优化搜索算法代价大（即使算一个简单的高次方程也得进行几千次的运算并且得到的往往是近似解）。即使为了解决原因2）的矛盾，找到一些等价的具备逐步逼近、搜索构造潜力的特征量，可能在大代价运算后得到一些非整数解。因此，采用非搜索优化的算法写程序是合适的。

4 程序的设计

程序的编写和运行环境：在Windows XP环境下用visual studio 2010 的Win32控制台应用程序环境编写控制台应用程序。在XP上运行。

工程文件说明及使用：visual studio 2010的Win32 控制台应用程序中有四个程序员主要使用的文件。分别是：tragetver.h， stdafx.h， stdafx.cpp，工程名.cpp。本次程序的工程名为2222222，主文件名字是2222222.cpp。程序在主文件中编写。

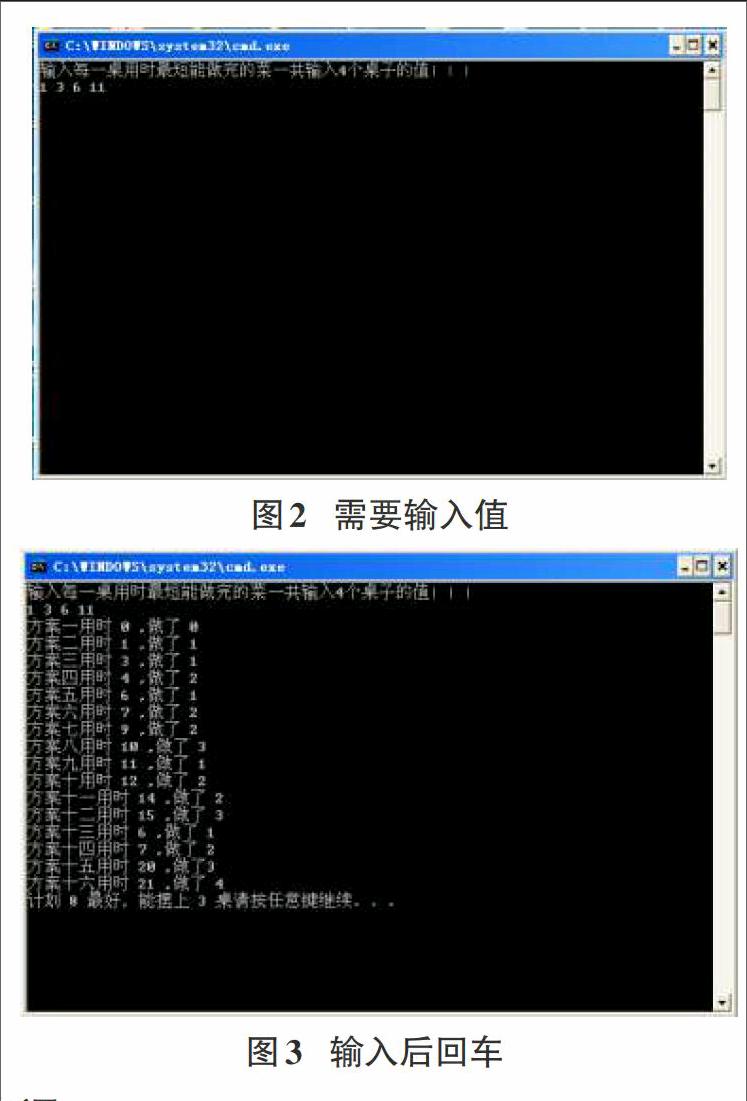
本程序假定有四张桌子，因此上菜可能计划是16种。程序流程设计如下：（4.1）定义若干int型变量（x、y分别表示0值和1值。desk数组容量为4，表示本轮各桌需求菜品用时最少的菜的时间值。recive_value数组容量为16，表示16种方案对应的本轮成功上菜的桌子数。Time数组容量十六，表示16种方案对应花费时间值。project数组容量为16，表示16种方案对应指标值，为1至16。其余int型变量均为过程保存变量、for循环控制变量或输出参数变量，此处不一一列举。）；（4.2）通过for循环令每个recive_value[i]=0（i=1…16）；（4.3）用printf语句提示用户输入，scanf语句令四个输入值存到desk数组中（如下图（1））；（4.4）纸上罗列每种方案的向量值（所有向量的每个位置不是x就是y），接下来的48行代码中每三行的内容分别是：（4.4.1）把某方案各位置向量值各位置的x或y相加存入对应recive_value[i] 中（i=1…16）；（4.4.2）把对应方案的向量值与desk数组组成的4维向量正交运算值存入对应Time数组；（4.4.3）用printf语句输出相应方案的描述信息；（4.5）使用for循环语句：内容是若某个recive_value值多于10，则令其为零；（4.6）编写三重嵌套for循环，实现两个冒泡排序，即令recive_value[15]和project[15]得到各自数组的最大值（recive_value在冒泡时进行的相邻位置值交换要携带project相邻位置值交换，这保证recive_value[15]的值和project[15]相对应，即recive_value[15]显示最大上桌数project[15]经交换得到现有指标值就是最大上桌方案的序号。）；（4.7）输出recive_value[15]和project[15]以及相关说明（如图3最后一行内容）。

数学模型和关键设计对应关系：根据（3.8）和第三节原因（2），本次目标应从16个方案的集合中取上桌最大recive_value。每个recive_value值相当于每个方案对应（3.8）不等式左边的值，（3.8）中ki均为1时。由于（3.9），应存在容量为16的数组Time保存每种方案对应的（3.9）不等式左边值。（4.4）目的是计算并保存每轮方案集合中各上桌值，同时也计算和保存了每种方案对应Time值；（4.5）把不满足（3.9）中上界值的对应recive_value数组值赋为0，这排除超过上界但上桌数巨大的干扰值方便（4.6）排序以求得16种方案中满足（3.8）的方案。应指出，定义project数组目的是说明方案i（project[i]值）对应录入每桌最小上菜时间后、排序前经过程序运算后的recive_value[i]值。

理解程序设计难点在于（4.6）如何保证排序结束后现有project[15]值在排序开始前所对应recive_value值就是三重嵌套for循环后的recive_value[15]值？给出分析过程：经典算法中排序算法的功能使得设计中可尝试定义数组把目标中最大值经排序定位到末尾输出，但有用信息不止一个而它们判断并被操作的时刻又不能轻易分开（存在破坏对应数组同步性可能），这说明若能揭示目标最大值和对应相关信息的有用关系是有可能在循环结束时令多种对应信息同步至末尾；若recive_value[i]比recive_value[i+1]大就在交换它们时自然也把对应位置project值进行交换，则之后在进行该操作时对应project[i]或project[i+1]的值是不对应数组序号的，由之前把具备期望recive_value值潜力对应project值交换造成；按此规则，随着recive_value两两交换，具备recive_value值潜力对应project值即使变化也依然向后推进并且该值所表示方案号初始对应的上桌数恰好等于此时同序号recive_value数组的值；基于以上分析，编写程序令两数组同时交换推进，理想结果会同步到各自末尾数组位置。

5 效果展示

6 结束语

1）通过3节最后部分论述得出：对于规模小的餐馆，该程序的实施可起到辅助管理决策的实际作用；

2）由于管理者需要按此程序的输出进行菜品出售，因此饭店管理者可凭此程序数据记录计算实际经营效果，这为日后食品制作流程改进和人事调度提供一定依据；

3）不足之处老板必须对照屏幕输出信息查找（4.4）中提到的方案录入程序时的纸张记录才能知道上菜方案。这是由于设计时间仓促造成。可在（4.4.3）中把当前方案信息加入输出语句中解决该问题；

4）通过4节第四段程序与模型的对应关系可发现本次设计把数学模型各部分拆分成方便程序表示和计算的流程进行编写，与2节论述的本文目的稳和。由此看出，本次编程没有偏离主题；

5）3节首段描述说明什么样的制度最有可能解决客户对上菜慢的不满，而程序的设计与结果符合3节提出的上餐流程，因此可以帮助管理者协调客户关系。

参考文献：

[1] 乐天. 遗传算法求解0/1背包问题的综述[J]. 浙江海洋学院学报：自然科学版， 2013， 32（1）： 71-74.

[2] Merkle R， Hellman M， Hiding Information and Signatures in Trapdoor Knapsack s[J]. IEEE Transactions on Information Thoery， 1978， 24（5）： 525-530.

[3] 王晓东. 算法设计与分析[M]. 北京：清华大学出版社， 2003.

[4] 周明，孙树栋. 遗传算法原理及应用[M]. 北京：国防工业出版社， 1999.