高校数学课教学改革方法研究

刘伟 ，丁小星

（公安海警学院 基础部，浙江 宁波 315801）

高校数学课教学改革方法研究

刘伟 ，丁小星

（公安海警学院 基础部，浙江 宁波 315801）

随着高等教育的快速发展，基础课教学改革呈现出空前的必要性和紧迫性。本文提出高校数学课程教学中几种教学方法和考核评价体系。通过这些方法在教学实践中的运用，力求提高学生的能力素质与创新意识，促进学生的个性发展和提高自主学习的能力。

数学；教学方法；评价体系

在当前高等教育中，高等数学、工程数学等基础课一直处于各专业课程体系的中心地位，也是很多工学和理学专业考研的必考课程。为适应学生素质的多层次性，高校数学的教学模式也呈现出多层次和多样化的特点。不同的培养层次、不同的专业，选择的数学专业课有所区别，对数学能力的要求也不尽相同，高等数学、工程数学等专业基础课却是它们共同必修的内容。基础理论之所以称为基础，是因为它确实是通向应用的桥梁。所以，如果要引进新课程或拓展新的前沿学科，必须先完善基础课的教学内容。任何教育改革都必须重视基础内容的教学。

一、课堂教学方法的多元化:改进高等数学教学方法的尝试

在公安现役院校中，数学课程一直是基础课程，一些专业的核心主干课程必须要依靠数学做支撑，数学教育也越来越受到重视。但是，笔者在教学实践中了解到还有很多的学生对数学有畏难情绪，学习方法存在误区，只担心考试不及格，甚至影响到毕业拿学位，对学习数学的兴趣不足。因此，如何改进数学课的教学方法，使学生对数学产生兴趣，是教师在教学当中首要解决的问题。教师在授课时首先要克服“满堂灌”的教学方式，运用灵活多样的教学方法，提升学生的学习兴趣。笔者结合十年来工作经验对一些教学方法进行了尝试：（一）讨论教学法[1]

培养思维方法是素质教育的核心目标之一。在高等数学教学中，通过讨论可以有效促进思维方法的培养和形成。例如，在我们的教科书中，概念、定理、公式在书上都是黑体标识在显要的位置，在教学中容易引起重视，但这也是学生难以掌握、却又是最为重要和基本的知识。研究表明，数学知识由于多而杂又不被经常用到，因而很容易被遗忘，但是数学思想方法却能被深深记住，并使我们终生受益。因此，我们在教学中使用讨论教学法，以加深学业生对基本知识的理解。例如，我们在学习导数的时候可以给学生提出一个加深认识极限思想的问题一起讨论——平均速度和瞬时速度。

一辆汽车从t0时刻到t时刻，位移函数为s(t)，平均速度

这个学生很容易答出，但是瞬时速度就回答不出来了。瞬时速度就是没有时间间隔的速度，这本身就是一个矛盾，怎么去理解这个问题。我们回想极限的思想，为了求出没有时间间隔的速度先给出一个时间间隔。当时间间隔比较小时，可以近似理解为匀速运动然后再用极限的思想把时间间隔足够变小，就是取极限，这样就得到了瞬时速度的公式，这是平均速度向瞬时速度的质的飞跃，在讨论中可以使学生对极限思想的认识得到进一步加深。

（二）故事教学法[2]

兴趣是最好的老师。如何培养学生的学习兴趣是教学的关键环节。高等数学内容抽象难懂，学生的学习兴趣淡漠，这给课堂教学增加很大难度。为改变这一现状，在教学过程中，把一些有趣的数学人物和数学故事融入到教学内容中去，用讲故事的方式作引导，这大大增加了学生的学习兴趣，同时加深对数学知识的掌握和对历史故事文化背景的了解，从而改善教学课堂氛围，实现学生对知识的掌握。

例如，我们在讲授“数学期望”——经常讲一个关于概率起源的小故事。主人翁是法国数学家费马，另一个是帕斯卡。1651年，法国贵族梅累向帕斯卡提出了一个关于赌注的分配问题。两个赌徒规定掷2个筛子，谁先掷出5次“双6”，谁就获得全部赌金。赌了很长，A掷出4局，B掷出3局，时间很晚了，他们都不想再赌下去了。那么，这个钱应该怎么分？是不是因为最早说的是满5局，而谁也没达到，所以就一人分一半呢？还是说A要多一点呢？但是多少合适，怎么分配呢？正确的分发是：掷出4次的拿这个钱的3／4，掷出3次的拿这个钱的1／4。为什么呢？假定他们俩再赌一局，或者A掷出，或者B掷出。若是A掷出满了5局，钱应该全归他；A如果没有掷出，即A、B各赢4局，这个钱应该对半分。现在，A赢、输的可能性都是1／2，所以，他拿的钱应该是1／2×1＋1／2×1／2＝3／4，当然，B就应该得1／4。这个问题可把他难住了，他苦苦思考了两三年，到1654年才算有了点眉目。于是他写信给的好友费马，两人讨论结果，取得了一致的意见：梅累的分法是对的。在他们这次的讨论中概率论中的一个重要基本概念——数学期望形成了。惠更斯把这则事件写成一本书叫《论赌博中的计算》（1657年），这就是概率论最早的一部著作。这就是用数学期望定价，于是概率发展了。利用故事去引入，学生便不会觉得枯燥，有利于提高学生对学习新学科的兴趣。

（三）探索教学法[3]

探索教学法是在学生对知识有一点基础认识的前提下，以问题为载体，以研究为导向，在教师的指导下，对问题进行构建研究，从而实现科学教育的一种教学方法。在教学过程中，教师起主导作用，学生是学习的主体，教师要构建合适问题指导学生作答，从而最终实现对有疑惑的知识的掌握。

例如，在做导数的题目时经常遇到这样一个问题：求函数y=xx的导数。有的同学把这个函数理解成幂函数y＇=xxx-1，有的同学把它理解成指数函数y＇=xx1nx，到底哪个答案是对的呢？其实这是一个幂指函数，正确方法利用对数的恒等变形y=ex1nx再求导

y＇=(ex1nx)＇=ex1nx(1nx+1)=xx(1nx+1)

或者也可以用对数求导法。

对函数y=xx两端取对数变形1ny=1nxx=x1nx，

所以可得y＇=y(1nx+1)=xx(1nx+1)。

我们用两种不同的方法得出同样的结果。经过和学生一起讨论，最终探索发现正确结果为上述两个错误解法的和。经过探索也能帮助学生了解到幂指函数和初等函数不同，也可以找到对幂指函数求导的规律，帮助学生加深认识。

（四）分层教学法[4]

大学数学课程的开设在大学一般是以大班授课的形式，教师很难照顾全部学生。就以我院为例，不同专业的教学大纲都不尽相同，就是同一专业的学生来自不同地区入校的，数学基础也存在较大差异，这给大班授课的教师提出了更高的要求。为了解决这一难题，我们采用分层教学法。分层教学法就是按智力、能力、学习成绩等分组、分层次的一种教学组织形式。我们在处理同一个知识点时可以对不同层次的学生提出不同的能力要求，使得基础差的学生能掌握知识，基础好的学生能利用更多的办法解决问题，达到融会贯通。

对于基础一般的学生，我们可以根据单调有界数列必有极限我们可以先来证明数列的单调性（显然单调递增），然后利用高中数学学习过的数学归纳法来证明数列的有界性。

1.u1

2.假设通项un＜2，下面来证明un+1＜2。

un+1=得证，这就证明了极限的存在性。

3.下面求极限。

un+1=等式两端求极限得

对于程度较好的学生，我们可以利用柯西收敛准则

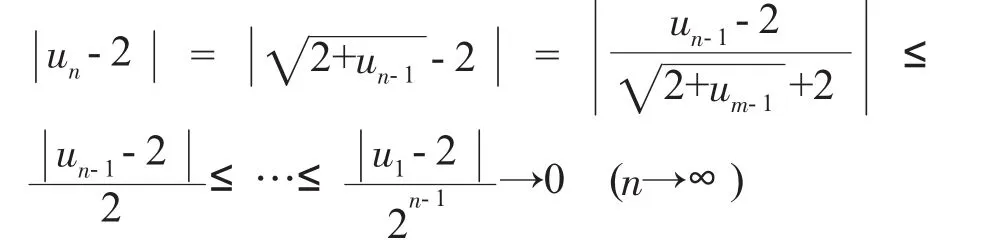
这构成一个压缩印象，可以得出极限为2.

（五）任务教学法

任务教学法是“学生中心，从学中做”的教学模式，它主张教育的中心应从教师和教科书转到学生。教师课前根据学生实际和教学内容，写好教学提案，给出学习任务，学生根据教师设计的教学任务，对任务的进行解剖、分析、讨论、查阅资料，明确学习目标，然后学生自主探索和互动、协作，找到完成任务的方法。通过完成任务，来实现知识建构，获得新知。

例如，在学习极限的课程时，教师提出教学任务：

极限的起源是什么时候？创始人是谁？他的主要贡献是什么？

1.诗句“一尺之锤，日取其半，万世不竭”体现的是什么思想？

2.0.999…和1哪个大？为什么？

3.无穷的意义是什么？关于无限循环小数比较大小高等数学和初等数学有什么区别？还能想到什么无限、无穷的例子吗？

学生根据具体问题搜集资料，积极思考，完成任务。最后在对任务讨论交流，加深对知识的掌握。

二、余论：建立良好的考核评价体系

从一定程度上讲，评价体系是教学的指挥棒在高等数学的教学过程中，课堂教学固然重要，但一个良好的考核评价体系也直接影响到教学效果。传统的高校课程考核体制存在很多弊端。具体表现为笔试多，谈话交流、课堂提问等考核方式少；基本知识考查多，素质能力考查少；终结性考核多，过程性考核少。这种陈旧的考核方式，无法准确考核出学生对知识真实的掌握情况，更无法了解到学生的数学能力和基本素质水平，影响了学生的学习积极性。既无法全面反映教学效果和教学质量，又背离了以人为本的教学理念，影响着学生能力素质的提高与个性的全面发展。为此，需建立合理的考核评价体系。

（一）理论和实践并重。弱化基本理论、基础知识的考核，加强对学生实践能力的培养。具体方式为布置平时作业、写阶段性课程小结、利用数学软件来解决实际问题。

（二）完善教师、学生多元评价主体，拓展评价活动的参与度。课程评价要改变以往由教师一人决定的方式，应该采用教师、学生相结合的多元评价方式。教师可以对学生进行公开和公平评价，反过来，学生也可以对教师的评价提出质疑，学生之间还互相评价，充分调动学生共同参与建立合理公正的评价体系。

（三）制定“量化评价”指标。为使考核评价落在实处，可制定制度化、规范化、可操作性的“量化评价”指标。指标给学生提供了一个有力、有效的指导，可以根据指标反映出的问题对症下药，努力改进，不断提高。

参考文献:

[1]傅苇.高等数学教学方法的探索与实践[J].大学数学，2007（12）：6-9.

[2]崔艳.高等数学“故事教学”探析[J].科教文汇，2014（10）：42-44.

[3]朱婉珍，陈笑缘.高等数学“问题研究教学法”探究[J].宁波大学学报（理工版），2004（9）：369-372.

[4]赵春元,李关民,王键闻,王娜.高等数学分层次教学改革与实践[J].沈阳工程学院学报（社会科学版），2009（7）：404-406.

On Teaching of Mathematics at University

LIU Wei,DING Xiaoxing
（China Maritime Police Academy,Ningbo 315801,China）

With the rapid developmentofhighereducation,thebasic courseteaching reform presents the unprecedented necessity and urgency.This paper proposes several kinds of teaching methods and examination evaluation system.Through the research of these methods,it strives to improve the quality ofthe students'ability and innovation consciousness,promotes personality development of students and improves the ability of autonomous learning.

math;teaching method;evaluation system

O1-4

：A

：2095-2384（2016）04-0034-04

（责任编辑 穆 静）

2016-10-30

刘伟（1981-），山东滕州人，公安海警学院基础部数学教研室讲师，主要从事数学实验教学、随机微分方程的研究。