基于卷积高斯窗的电能计量研究

沈放，陈艳，黄灿英，谢风连

（南昌大学科学技术学院，江西南昌 330029）

基于卷积高斯窗的电能计量研究

沈放，陈艳，黄灿英，谢风连

（南昌大学科学技术学院，江西南昌 330029）

结合卷积高斯窗和傅里叶变换实现电能计量分析，利用高斯窗函数良好的时频分辨能力，可以准确辨识电能信号中不同的谐波分量，完成电能精确估算。实验仿真电能信号含有5阶谐波分量，对比了高斯窗函数，卷积高斯窗函数对仿真电能信号不同阶次谐波分量的频率、幅度和相位的数值估计误差，验证了卷积两次的高斯窗函数的性能最优，其对于电能信号谐波参数的估计相对误差均在0.1‰以下。

高斯窗；卷积；电能计量

现代化电网建设的研究重点越来越多地侧重于智能化、自动化的电能供应，电力传输以及故障识别控制方面[1-2]。伴随着不断增长的工业、家庭用电量，准确的电能计量成为电力供给领域需要解决的重要问题之一[3－6]。然而，电能传输过程中的干扰及各种非线性电子元件的使用，使得电能信号本身具有多个不同成分的谐波分量。这些谐波分量无法使用，却属于传输的电能，对这些信号进行计量以及抑制，从而控制电能质量，提高实际有效电能消耗的估计，成为电力计量领域的研究热点[7-9]。

显然，若能够准确地识别出谐波信号，并计算各个谐波电能信号的频率、幅度和相位，便可实现电能消耗的精确测量。基于傅里叶变换及其快速算法的各种方法是目前解决这类问题的主要算法，这是因为傅里叶变换能对周期性的频率信号起到聚焦作用，不同的频率成分可被有效分离[10-11]。通过计算机或相关的硬件电路，采用数字信号处理方法，不同的研究者已经对识别谐波信号提出了系统地解决策略。然而，单纯采用快速傅里叶变换算法实现频谱估计，存在数字点长效应，即用来进行数字傅立叶变换的点数和采样频率之间不能除尽，从而存在需要估计的谐波频率分量没有与其对应数字频率点投影位置的问题，出现频谱切迹，频谱分裂现象。为了解决上述问题，结合窗函数傅里叶变换谱线估计算法，以及卷积窗函数的傅里叶变换谱线估计算法被提出和验证能够更加有效地分析出信号的谐波成分[3－8]。这些方法尽管取得了较好的效果，却只是考虑了窗函数对频谱修正具有作用，并未考虑窗函数自身的时频分辨能力。实际上，现代信号分析已经证明，高斯函数及其对应的窗函数具有最优的时频联合分辨能力。因此，本文主要研究基于高斯窗体的电能计量算法，并分析与展示所述方法的有效性。

1 窗函数的时频特性

窗函数设计是数字信号处理的经典技术之一，其一般用于产生特定通带或阻带的滤波器，电能计量研究的重点就是识别电能信号中夹杂的多种不同成分的频率分量，通过设计窗函数，可以提高对电能谐波信号的辨识能力[1-4，10-11]。常用的窗函数包括：矩形窗函数、三角窗函数、汉明窗函数、汉宁窗函数、布莱克曼窗函数以及高斯窗函数等。其中，矩形窗和三角窗形式简单，却存在更加突出的频谱泄漏问题，目前研究更多的是其他几种窗函数[10]。具体离散表达形式如下：

汉宁窗

汉明窗

布莱克曼窗

高斯窗

式中：a为方差。

图1展示了几种常规窗体的时域和频域特性，其中蓝色曲线代表布莱克曼窗，红色曲线代表汉明窗，高斯窗由绿色曲线描绘。在相同窗长N下可看出，高斯窗的频谱具有最小的旁瓣，能够最小化频谱泄漏的影响，从而产生更好的时频聚焦能力。

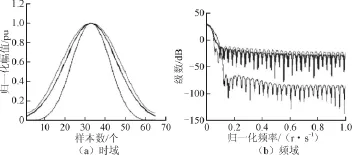
图1 不同窗函数的时域，频域特性Fig.1 Time domain and frequency domain characteristics of different window functions

卷积高斯窗函数是对高斯窗函数进行卷积所得到的，高斯窗函数相比于其他窗函数，在卷积计算时具有其独特的计算优势，因2个高斯窗函数的卷积结果，可直接由2个高斯窗的方差直接计算得到。其具体表达式为式（5）和式（6）：

g1（x）=分别为2个不同的高斯函数

表示卷积高斯函数

卷积高斯窗函数本质依然是高斯窗函数，通过卷积可动态调节高斯窗的窗体宽度和方差大小。由图2可知，绿线表征的卷积高斯窗具有更加有效的频谱旁瓣抑制效果。

图2 高斯窗函数与卷积高斯函数的时域，频域特性Fig.2 Time-domain and frequency-domain characteristics of Gaussian window function and convolution Gaussian function

2 仿真实验

为了验证本文的卷积高斯窗函数特性，本文对仿真电能信号进行谐波分析，其具体的离散模型表达为

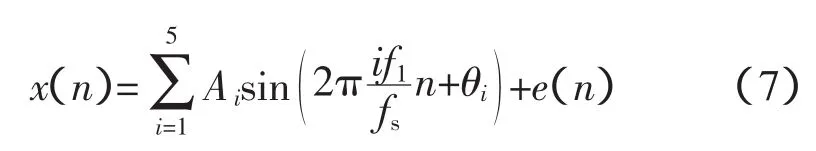
其中基波频率f1为50.2 Hz；采样率fs为1 500 Hz，θi为初始随机相位；Ai为各次谐波的幅度数值；e（n）表示一个白噪声；实际每次采集的样本点数据长度N为512点，基波和各次谐波的幅值（为无单位数值）与相位如表1所示。采用文献[10-11]中的双峰谱线修正算法结合不同卷积次数的高斯窗函数，对上述仿真信号进行估计，并对比各次谐波的参数估计误差。

图3展示了仿真电能信号，其具有多次谐波，可在其波形中观测到除去固有基波周期外的多种抖动。本文采用的原始高斯窗函数为方差2.5的高斯窗函数，用来进行谐波频率估计的叠加窗函数分别是原始高斯窗函数、卷积1次以及卷积2次的高斯窗函数。对应的处理得到的仿真电能信号的频谱效果图如图4—图6所示。

表1 带谐波的电能仿真信号参数Tab.1 Parameters of power simulation signal with harmonic

图3 仿真电能信号Fig.3 Simulated power signal

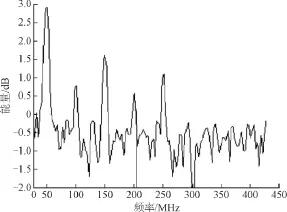
图4 原始高斯窗函数处理的仿真信号频谱Fig.4 The spectrum of the simulated signal processed by the original Gaussian window function

图5 卷积1次高斯窗函数处理的仿真信号频谱Fig.5 The spectrum of the simulated signal processed by one convoluted Gaussian window function

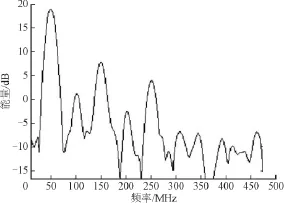
图6 卷积2次高斯窗函数处理的仿真信号频谱Fig.6 The spectrum of the simulated signal processed by convoluted two Gaussian window function

图4—图6均显示了在50 Hz附近以及50 Hz的倍频为100，150，200，250附近的位置上具有对应的频谱峰分布。然而在图4中，各个谱峰顶部均有明显的切迹，本来在对应50 Hz附近只应存在一个谱峰，现在却出现了频谱峰分裂现象，视觉上类似2个频谱峰相叠加。采用卷积高斯窗，随着卷积次数的提升，可以从图5和图6中看出，原本存在的频谱峰的切迹消失，这对于准确估计频谱峰的位置，以及计算相应的幅度和相位至关重要。

表2—表4展示了采用不同高斯窗函数进行谐波估计的误差。可以看出，采用2次卷积高斯窗分析的结果明显要优于其他2种，其对于任意谐波的整体识别误差在0.1%以下，且具有良好的识别精度和准确性，体现了卷积高斯函数对于准确谐波辨识的价值。

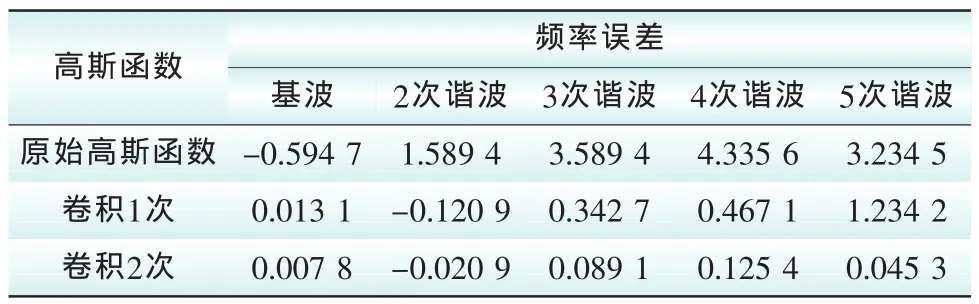
表2 不同卷积高斯函数的谐波频率参数估计比较Tab.2 Comparison of harmonic frequency parameters estimation for different convolution Gaussian functions‰

表3 不同卷积高斯函数的幅度参数Ai估计比较Tab.3 Comparison of amplitude parameter Ai estimates for different convolution Gaussian functions ‰

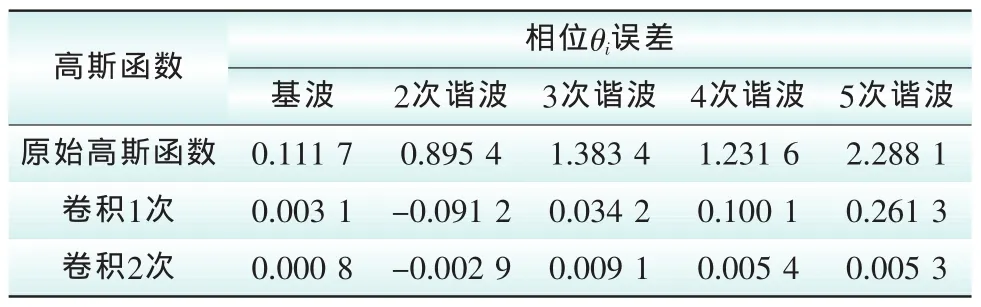
表4 不同卷积高斯函数的相位θi参数估计比较Tab.4 Comparison of phase parameter θiestimates for different convolution Gaussian functions ‰

3 结语

电能计量是电力系统的重要研究领域，本文提出的卷积高斯窗可有效提高电能中谐波分量识别的准确度，从而为精确电能消耗提供有效技术支撑。仿真验证了本文提出的卷积高斯窗的可行性和高效性，进一步研究重点在于将上述方法结合进入电能无功补偿设备，以及有功消耗计量设备之中，实现电能消耗的实时计量分析。

[1]王桢.电网谐波对电能计量的影响[J].电器与能效管理技术，2012（22）:40-45.WANG Zhen.The influence of harmonic on electric energy metering[J].Electrical Appliances and Energy Efficiency Management Technology，2012（22）:40-45（in Chinese）.

[2]朱彩虹，黄清秀，黄纯.间谐波存在时的电能计量方法研究[J].电力系统保护与控制，2015，43（9）:15-20.ZHU Caihong，HUANG Qingxiu，HUANG Chun.Study on the method of energy metering in the presence of interharmonics[J].Power System Protection and Control，2015，43（9）:15-20（in Chinese）.

[3]禹化然.基于GPS同步时钟载波电源的分布式同步测量系统的研发[D].杭州:浙江大学，2010.

[4]胡君慧，齐晓光.考虑低电压穿越影响的双馈感应发电机谐波电流特性[J].电网与清洁能源，2015，31（7）: 106-113.HU Junhui，QI Xiaoguang.Harmonic current characteristics of doubly-fed induction generators with low voltage ride-through[J].Power System and Clean Energy，2015，31（7）:106-113（in Chinese）.

[5]张晓冰，李云辉，房国志.非平稳畸变信号条件下电网信号建模[J].中国电机工程学报，2014（16）:2721-2728.ZHANG Xiaobing，LI Yunhui，FANG Guozhi.Signal modeling of power system under non-stationary distorted signal condition[J].Proceedings of the Chinese Society for Electrical Engineering，2014（16）:2721-2728（in Chinese）.

[6]张晓冰，王会龙，姜世超.基于信息熵评价指标的多小波畸变电能计量[J].哈尔滨理工大学学报，2016，21（1）:57-61.ZHANG Xiaobing，WANG Huilong，JIANG Shichao.Multiwavelet distortion energy metering based on information entropy evaluation index[J].Journal of Harbin University of Science and Technology，2016，21（1）:57-61（in Chinese）.

[7]岳靓婧.基于提升小波变换的畸变信号条件下电能计量装置研究[D].长沙:湖南大学，2012.

[8]王凯红.不确定度理论在电能计量和局放信号处理中的应用研究[D].北京:华北电力大学，2015.

[9]王洋洋，原明亭.电网畸变信号下电能的计量方法研究[J].青岛大学学报（工程技术版），2016，31（3）:29-34.WANG Yangyang，YUAN Mingting.Study on the measurement method of electric energy under the distorted signal of power grid[J].Journal of Qingdao University（Engineering and Technology Edition），2016，31（3）: 29-34（in Chinese）.

[10]李得民，何怡刚.基于Nuttall窗四谱线插值FFT的电力谐波分析[J].电力系统保护与控制，2016，44（3）:64-71.LI Demin，HE Yigang.Power harmonic analysis based on Nuttallwindow four-line interpolation FFT[J].Power System Protection and Control，2016，44（3）:64-71（in Chinese）.

[11]张宝，易吉良，姜建伟，等.基于FFT与小波变换的机车谐波电能计量[J].湖南工业大学学报，2013，27（5）:58-62.ZHANG Bao，YI Jiliang，JIANG Jianwei，et al.Based on FFT and wavelet transform of locomotive harmonic energy measurement[J].Journal of Hunan University of Technology，2013，27（5）:58-62（in Chinese）.

Study on Energy Measurement Based on Convolution Gauss Window

SHEN Fang，CHEN Yan，HUANG Canying，XIE Fenglian
（College of Science and Technology，Nanchang University，Nanchang 330029，Jiangxi，China）

In this paper，electrical energy measurement analysis is realized by combining convolution Gauss window method and Fourier transform.Taking advantage of the best time-frequency resolution of Gauss window function，the proposed method can accurately identify differentharmonic components in electrical signals and complete the estimation of electrical power.The experimental simulation containing an electrical signal of 5 harmonic components compares frequency，amplitude and phase estimation errors of different orders of harmonics by Gauss Window function and convolution Gauss Window function to verify that the second convolution Gauss window function has the best performance，where the relative estimation errors of electrical signal parameters are all below 0.1‰.

Gauss window；convolution；electrical energy measurement

2016-04-02。

沈 放（1974—），男，硕士，讲师，研究方向为电力电子应用技术、信息与应用技术。

（编辑 张晓娟）

国家自然科学基金项目（61372071）。

Project Supported by the National Natural Science Foundation of China（61372071）.

1674-3814（2016）12-0069-04

TM769

A