递进式讲授教学法在Nyquist稳定判据教学中的设计及应用

张 倩

(安徽大学 电气工程与自动化学院， 安徽 合肥 230601)

递进式讲授教学法在Nyquist稳定判据教学中的设计及应用

张 倩

(安徽大学 电气工程与自动化学院， 安徽 合肥 230601)

本文采用递进式讲授教学法对Nyquist稳定判据的教学进行了探讨。从线性系统稳定的充分必要条件出发，用递进式讲授方式，穿插探究式教学方法，以step by step的方式逐层推送，最终得出Nyquist稳定判据。教学实践证明，该方法能激起学生的求知欲和主观能动性，达到对知识点的深刻理解和掌握。

递进式讲授；Nyquist稳定判据；探究式教学方法

0 引言

“自动控制理论”是自动化专业和电气专业的重要基础理论课，同时也是测控、电子信息工程、通信工程、导弹工程等专业的必修课程。它是学习“现代控制理论”、“过程控制”等本科后续课程的基础，也是学习“线性系统理论”、“自适应控制”等研究生课程的基础，还是工业过程控制与优化设计的理论依据[1,2]。

在“自动控制原理”的教学中，频域分析部分占有很大的比重，知识多，难度高，也是学生普遍反映较难理解和接受的部分[3]。笔者针对“自动控制原理”频域分析教学部分中的重难点—Nyquist稳定判据， 研讨了递进式讲授方式在该知识点课堂教学中的应用，逐次递进的过程中，辅以探究式教学方法，由浅入深地为学生引入相关知识，得到频率域稳定判据的结论。经比较分析多种教学方法后，得出了采用该方法设计本课程内容教学效果会大大提高的结论。

1 课前准备及教学思路

复变函数中的幅角原理是Nyquist稳定判据的数学基础，笔者在在上课之前预先布置给学生进行回顾，作为课前准备和后续学习的知识储备。上课时通过简介或者提问的方式进行幅角原理掌握和理解程度的确认。

Nyquist稳定判据的教学思路如图1所示。

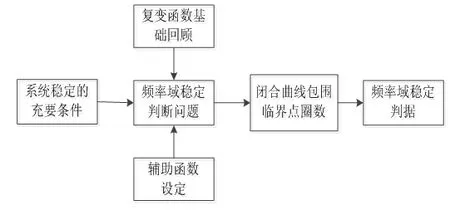
图1 Nyquist稳定判据的教学思路分析图

2 递进式讲授教学法的课堂设计

教学目标：频率域完成稳定性分析，得出Nyquist稳定判据。

方法： 从线性系统稳定的充要条件出发，逐步得出根据幅相频率特性曲线及Nyquist回线共同构成的Nyquist曲线判断稳定性的判据。

分析工具：幅角原理、辅助函数。

递进式讲授教学法的课堂该设计如下。

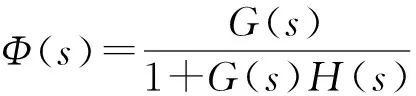
Step2：Φ(s)=M(s)/N(s)的特征方程N(s)=0是否存在有正实部的根在s右半平面？

Step3：引入辅助方程F(s)=1+G(s)H(s)。

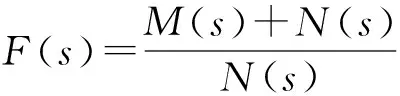
探究：那么Step2的问题就是转化为F(s)是不是有零点在s的右半平面？

Step4：引入幅角原理。

用一个无穷大的曲线Γ包围s的右半平面。由幅角原理中，要求闭合曲线不可穿过开环传递函数的任一个零点和极点，所以需要根据开环传递函数的极点分布进行三种情况的讨论。

Step5: 探究：曲线Γ包围的区域内有没有F(s)的零点？闭环极点中位于s右半平面的个数Z是不是等于零？

Step6:由幅角原理，曲线Γ映射为闭合曲线ΓF，讨论ΓF包围原点的圈数。由辅助函数，问题转化为ΓGH包围(-1,j0)点的圈数R。进一步转化为：半闭合曲线ΓGH穿越(-1,j0)点左侧的次数。

Step7：讨论：半闭合曲线ΓGH的三种情况。对图2(a)ΓGH即对应开环幅相曲线;对图2(b)(c)ΓGH除开环幅相曲线还有Nyquist回线的补画。图2(b)的情况下，从G(j0+)H(j0+)逆时针补画v×90°，顺时针标注；图2(c)的情况下，从G(j0+)H(j0+)逆时针补画v×180°至G(j0-)H(j0-)，同样顺时针标注。

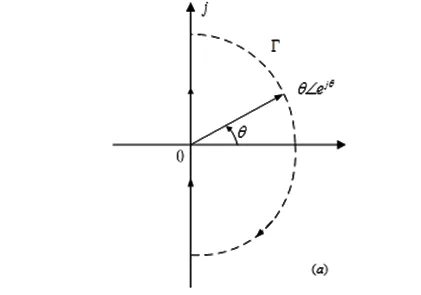
(a) G(s)H(s)无虚轴极点时

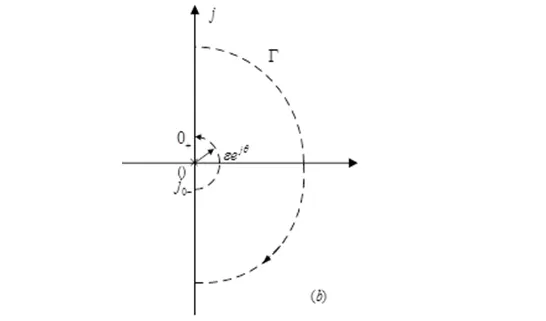
(b) G(s)H(s)极点于原点时

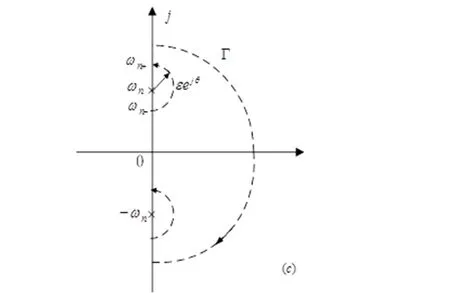
(c) G(s)H(s)极点于虚轴时图2 s平面的闭合曲线

Step8：Nyquist稳定判据。

反馈控制系统稳定的充分必要条件是半闭合ΓGH曲线，不穿过(-1,j0)点且逆时针包围临界点(-1,j0)点的圈数R等于开环传递函数的正实部极点数P。

3 教学效果对比

为验证递进式讲授教学法对Nyquist稳定判据知识点的教学效果，笔者特意对比了采用该教学方法的2013级电气工程专业学生与采用普通教学方法的2012级学生在类似情况下的学习成绩。

在2015-2016学年对Nyquist稳定判据的教学采用了文中所提出的教学方法的2013级学生与2014-2015学年没有采用该方法教学的2012级学生，在期末考试中，对该知识点相关考题的得分分布情况列示于表1。

表1 Nyquist稳定判据得分情况对比

(注：两个学期的期末考试中，该知识点的满分均为15分。)

由表中数据可见，采用新型递进式教学方法后，学生对该频域理论中的知识点掌握程度有明显的提高，验证了本方法的有效性。

3 结语

在我校电气工程与自动化学院的2012级和2013级电气工程专业的4个不同年次和班次的学生中，运用递进式讲授教学法与传统的教学方法进行比较的结果证明，学生在递进式教学的引导下，思路清晰，注意力集中，学习兴趣和主动性明显提高。达到了良好的预期效果。

[1] 武庆东，孙志辉. 自动控制理论基本概述 [J]. 北京：中国科技论坛， 2011，vol1：87-88

[2] 潘东波，刘枫，张渝， 周雪莲，对《自动控制原理》课程教学方式的探究[J]. 重庆：西南师范大学学报，158-160

[3] 丁世宏，杨年法，赵德安，马莉. “自动控制原理”课程的频域部分教学探讨[J]. 南京:电气电子教学学报， 2012， 34(3)：106-108

The design and application of progressive education method to the teaching of Nyquist stability criterion

ZHANG Qian

(DepartmentofElectricalEngineeringandAutomation，AnhuiUniversityofScienceandTechnology,Hefei230601，China)

This paper introduces the progressive education method into the teaching of Nyquist stability criterion. Based on the stability necessary and sufficient condition of linear sytstem, the progressive and inquiry education methods are applied, finally the Nyquist stability criterion is obtained step by step. By teaching practice, it is proved that this method is able to arouse students' curiosity and initiative, keep the attention and the activity. As a result, the deep understanding and mastery of the knowledge point are achieved.

progressive education method; Nyquist stability criterion; inquiry education method

2016-11-27;

2016-01-25 基金项目：安徽省重大教学改革研究项目(2013zdjy038)；安徽大学教改研究项目(ZLTS2015064)

张 倩(1964-)，女，博士，讲师，主要从事自动控制理论、系统辨识和切换系统的教学和研究工作，E-mail：qianzh@ahu.edu.cn

TP13；G642

A

1008-0686(2016)05-0069-03