互联系统建模方法教学探索

李 斌， 赵 敏， 杨 欣， 陈德芮

(重庆大学 自动化学院， 重庆 400044)

互联系统建模方法教学探索

李 斌， 赵 敏， 杨 欣， 陈德芮

(重庆大学 自动化学院， 重庆 400044)

互联系统的建模是“自动控制原理”课程重要的教学内容。本文采用互联系统建模实例，以代数图论观点，揭示互联系统建模问题实质，导出互联系统物理描述与逻辑关系描述的相互关系表达式。并用Matlab编程实现了互联系统的自动建模。仿真结果表明，该方法反映了时代特征，是一种互联系统建模教学的有效方法。

互联系统建模；框图化简；梅逊公式

0 引言

互联系统建模是“自动控制原理”课程重要的教学内容。正如系统的定义描述的：系统是具有特定功能的，既相互作用，又相互制约的若干部分组合而成的有机整体。互联系统的描述包括各部分的物理描述和各部分间连接的逻辑描述。在已知各部分物理描述后，建模的重要一步就是寻找各部分间的逻辑描述，以及各部分物理描述与逻辑描述的关系，进而建立完整的互联系统模型。

目前，在教学过程和教材编写上，互联系统建模部分主要介绍动态框图化简和信号流图导出的Mason公式两种方法的应用，均未涉及方法的原理介绍[1-3]。这给学生学习和掌握相关内容增加了难度。随着互联系统规模的扩大，上述方法的缺点显现，很难用其建立大型复杂互联系统模型。这成为教学中急待解决的问题[4,5]。

有鉴于此，本文从代数图论的观点，揭示了互联系统建模实质，导出了互联系统物理描述与逻辑描述之间的关系；并编程实现了互联系统模型生成。与现有教学方法相比，本方法易被接受，便于计算机实现，是一种互联系统建模有效的教授方法。

全文共分五部分。第一部分给出互联系统建模实例；第二部分导出互联系统模型表达式；第三部分分析互联系统模型结构；第四部分介绍互联系统建模计算机实现；第五部分结论。

1 互联系统建模实例

互联系统建模实例如图1所示。其中，G1、G2、G3、G4、H1、H2为系统各环节的物理描述。它们既可以是各部分的传递函数，也可以是物理描述符号。R、C分别表示互联系统的输入和输出。

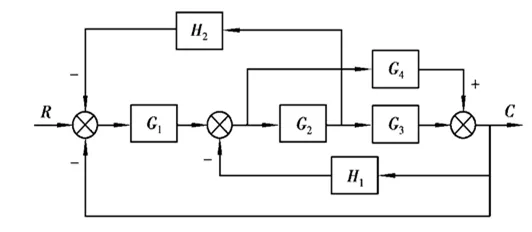
图1 互联系统建模实例

为分析方便，各环节的输入输出分别用r1、r2、r3、r4、rh1、rh2；c1、c2、c3、c4、ch1、ch2表示。简写为向量形式，即：

r=(r1r2r3r4rh1rh2)T

c=(c1c2c3c4ch1ch2)T

在此基础上，系统环节的集成可表为

c=G·r

(1)

其中

G=diag(G1G2G3G4H1H2)称为系统环节集成矩阵。

本实例的问题是：如何求出系统外部输入输出间的关系。

2 互联系统模型推导

为获得互联系统一般模型，假定系统有l个外部输入，m个外部输出，即R为l维列向量，C为m维列向量；n个内部环节。分析系统各环节输入端信号可得

r=Ln×nc+Mn×lR

(2)

其中，

矩阵L被称为系统环节逻辑矩阵；M被称为矩阵系统外输入逻辑矩阵。

将上述的式(2)代入式(1),整理得

c=(I-GL)-1GMR

(3)

由于G、L、M三个矩阵已知或可通过分析得出，故式(3)描述了系统各环节输出与系统外部输入间的关系。而系统的外部输出就包含其中，或为c某些元素的组合。将此组合逻辑记为Pm×n，称为系统输出逻辑矩阵。其定义为

则

C=R(I-GL)-1GMR

故

Φm×l@P(I-GL)-1GM

(4)

上式即为互联系统的模型。

3 互联系统模型分析

分析式(4)可知，互联系统的模型包含了描述系统物理特性的系统集成矩阵G，描述系统连接逻辑的系统环节逻辑矩阵L，矩阵系统外输入逻辑矩阵M和系统输出逻辑矩阵P。因此，互联系统的模型是系统物理描述和逻辑描述共同构成的整体。

从上述推导过程可见，在作出相关矩阵定义的基础上，求取互联系统模型的实质就是求取一组代数方程的解。由图论可知，对于单连通互联系统有det(I-GL)≠0，因此矩阵(I-GL)-1存在。故式(4)模型存在。

式(4)模型各元素具有深刻的图意义。对此，Mason已作了图解释，这里不再重复。教材中的框图化简规则，实质就是将解方程的过程图形化。

与现有教材介绍的方法比较，本方法揭示了互联系统建模实质，概念清晰，便于掌握，特别适合计算机实现。故称其为互联系统建模的代数图论法。

4 互联系统建模计算机实现

在式(4)模型的基础上，要实现计算机自动模型生成的一个关键是给系统各环节准确编号。参考Matlab的connect函数，式(4)模型计算机算法的关键步骤是：①定义环节集成矩阵；②用稀疏矩阵表示外输入逻辑、环节连接逻辑和外输出逻辑；③将上述三个逻辑矩阵自动转换为对应逻辑矩阵M,L,P；④生成系统模型，求取系统输出。

为使算法既适应各环节为已知传递数，又适应于有符号表示的环节，程序引入符号定义和计算。

以下是实例系统计算机建模的算法程序段。

syms G1 G2 G3 G4 H1 H2 R C

G = diag([ G1, G2, G3, G4, H1, H2, 1 ]);

% 互联系统环节的集成矩阵；in = [ 1 ]; % 外部输入位置；列数为外输入个%数；

ot = [ 3 4 ]; % 外部输出位置；列数为外输出个%数；

%系统连接矩阵的稀疏矩阵表示减少输入量，%表达更直观；

%其中，行数为系统的环节个数；列数为：最%大环节输入个数+1. 即第1列是个环节编号。

x = [ 1 -5 -7;

2 1 -6;

3 2 0;

4 1 -6;

5 2 0;

6 3 4;

7 3 4 ];

%负号表示信号负极性连接。

k = size(x,2); % 确定连接矩阵列数；

n = size(G,2); % 确定系统环节数；

I = eye(n); % 产生n阶单位矩阵；

L = zeros(n); %定义环节连接逻辑矩阵；

%自动生成系统连接逻辑矩阵；

for i = 1:n

% 共n行；按行逐列检查，判断；

for j = 2:k

if x(i,j) ～= 0

for p = 1:n

if ( abs(x(i,j)) == p ) & ( x(i,j) > 0 )

L(i,p) = 1;

end

if ( abs(x(i,j)) == p ) & ( x(i,j) < 0 )

L(i,p) = -1;

end

end

end

end

end

n1 = size(in,2); [ l1, l2 ] = size(ot);

M = zeros(n,n1); P = zeros(l1,n);

for i = 1:n1

for j = 1:n

if in(i) == j;

M(j,i) = 1;

end

end

end

for i = 1:l1

for k = 1:l2

for j = 1:n

if ot(i,k) == j;

P(i,j) = 1;

end

end

end

end

B = I - G*L;

A1 = inv(B);

V = P*A1*G*M;

C = V*R

说明：为简化输出表达，G中增加增益1的环节，V表示Φ。程序运行结果如下。

C =(G1*R*(G4 + G2*G3))/(G1*G4 + G4*H1 + G1*G2*G3 + G1*G2*H2 + G2*G3*H1 + 1)

这正是所求实例的动态模型。

5 结语

本文对互联系统建模教学方法进行了探讨。以代数图论观点，揭示了互联系统建模的实质；给出并分析了互联系统模型公式和结构；定义此方法为互联系统建模的代数图论法。文中给出的计算机实现程序引入符号运算，增强了算法的适应性。文中模型推导及仿真表明：该方法概念清晰，运算简单，易于掌握，有助教学；特别适合计算机实现。综合上述，代数图论法是一种有效的互联系统建模方法，这为互联系统建模教学提供了一种新的思路。

[1] 胡寿松，自动控制原理(第五版)[M]，北京：科学出版社，2007.6

[2] Richard C. Dorf, 现代控制系统(第十一版)[M]， 北京：电子工业出版社，2009.6。

[3] Mason S.J., Feedback Theory-Further Properties of Signal Flow Graphs[J], IEEE Journals & Magazines, Proceedings of the IRE, 1956, Volume: 44, Issue: 7, pp: 920 - 926.

[4] 郑志波,向农,谈顺涛,梅逊公式的CAI软件设计, [J],南京：电气电子教学学报．2004，26(3):55-62.

[5] 曾建平,雷宏,系统传递函数的矩阵求解法[J], 太原：太原机械学院学报,1991,12(2):65-72.

Teaching Exploration of Modeling Method of Interconnected System

LI Bin, ZHAO Min，YANG Xin，CHEN De-rui

(schoolofAutomation，Chongqinguniversity，Chongqing400044，China)

The modeling of the interconnected system is an important teaching content in the course of Principles of Automatic Control, This paper uses an example to reveal the essence of the problem of modeling the interconnected system in algebraic graph theory, and the relationship between the physical description and the logical description of the interconnected system is derived. The automatic modeling of the interconnected system is realized by Matlab programming. The simulation results show that this method reflects the characteristics of the times and it is an effective method for modeling teaching of interconnected systems.

interconnected system modeling，block diagram reduction，Mason's signal-flow formula

2015-10-19;

2016-02-23 基金项目：重庆大学项目(2013Y04)

李 斌(1958-)，男，博士，副教授，主要从事自动控制理论教学及导航制导研究工作，E-mail：lzbymcqc@sohu.com

G642.0

A

1008-0686(2016)05-0065-04