逻辑函数化简的教学难点与应对方法

杨 静

(武汉大学 电子信息学院， 湖北 武汉 430072)

逻辑函数化简的教学难点与应对方法

杨 静

(武汉大学 电子信息学院， 湖北 武汉 430072)

逻辑函数化简是“数字逻辑电路”课程的基础内容。教学中发现，学生使用卡诺图化简时常常找不到所有的逻辑相邻项，在理解逻辑函数的约束项和任意项的文字描述时也存在困难。本文采用立体图形表示逻辑函数，方便寻找逻辑相邻项，并以交通信号灯电路为例，解释了约束项和任意项的含义。

逻辑函数化简；约束项；任意项

0 引言

逻辑函数化简是“数字逻辑电路”课程教学中的基础内容[1-2]。常用的逻辑函数化简方法包括公式化简法和卡诺图化简法。公式化简法使用不受任何条件限制，但没有固定步骤可循，要求学生熟练运用各种公式和定理，还要有一定的运算技巧和经验，难度较大。卡诺图化简法简单直观，而且有一定的化简步骤可循[1]。但是，教学中发现，学生使用卡诺图化简逻辑函数，尤其是变量数较多时，常常难以找出所有的逻辑相邻项，使得化简不充分，得不到最简式。其主要原因是二维平面卡诺图没有充分展现最小项的逻辑相邻关系，学生在化简时需要找出如上下、左右两端闭合相邻，中心轴对称相邻等没有直观显示的相邻关系。

文献[2]使用立体图形表示一至四变量逻辑函数，逻辑相邻关系一目了然，但是并未将此图形用于函数化简。本文给出一种用立体图形表示及化简逻辑函数的方法，相比卡诺图化简法更为直观，更容易找出所有的逻辑相邻项。

约束项和任意项是两类特殊的最小项，统称为无关项。虽然它们在逻辑函数化简时的处理方法相同，但含义不同。为了正确表示逻辑问题，必须明确这两个概念的含义。虽然已有相关文献使用电路举例法解释这两个概念，但此部分内容为课程基础内容，采用课程后面才能学到的译码器等复杂电路进行举例说明并不合适，会增加学生的理解难度[3-4]。本文以简单的交通信号灯电路为例，说明这两个概念的含义。

1 基于立体图形的逻辑函数化简

1.1 逻辑函数的立体图形表示法

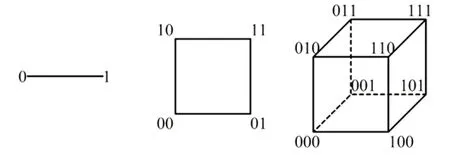
图1画出了一到五变量最小项的立体图形。每个端点代表一个最小项，端点附近标注了使这个最小项为1的变量取值。将逻辑函数化为最小项之和的形式后，在立体图形上与这些最小项对应的端点上画上圆圈，就得到了表示该逻辑函数的立体图形。

由于一个立方体只有八个端点，最多表示八个最小项，因此四变量最小项用两个立方体表示，五变量最小项用四个立方体表示。立方体下面标注的数值和端点附近标注的数值一起表示使该端点对应的最小项为1的变量取值。例如，图1(d)中左侧的立方体上，画上圆圈的端点标注的数值为101，此立方体下方标注的数值为0，所以使该端点对应的最小项为1的取值应当是0101；右侧的立方体上，画上圆圈的端点标注的数值为100，此立方体下方标注的数值为1，所以使该端点对应的最小项为1的取值应当是1100。

图1所示的立体图形中，每条线段两端的最小项逻辑相邻，可以合并为一项并消去一对因子；每个正方形的四个端点逻辑相邻，可以合并消去两对因子；每个立方体的八个端点逻辑相邻，可以合并消去三对因子。几何相邻的立方体也是逻辑相邻的。例如，图1(d)的两个立方体逻辑相邻，图1(e)标注为00的立方体和01、10这两个立方体相邻，而和标注为11的立方体不相邻。相邻立方体处于相同位置的端点、线段、正方形也是逻辑相邻的，可以合并消去一对、两对、三对因子。相邻立方体合并可以消去四对因子。

1.2 基于立体图形的化简举例

下面以五变量最小项的逻辑图形为例，说明基于立体图形的化简方法。

例：化简如下逻辑函数[1]。

Y=(AB′C′D+AC′DE+AB′DE′+AC′D′E)′

(1)

首先将逻辑函数化为最小项之和的形式，

Y=(m2+m6+m17+m18+m19+m22+m25+m27)′

(2)

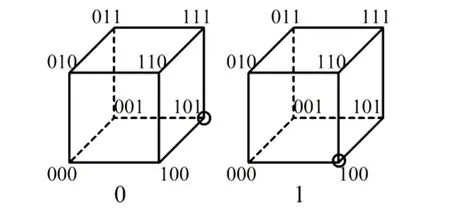
将上式括号内没有包含的最小项在立体图形中的位置画上圈，得到如图1(e)所示的图形。

观察发现，图1(e)中小正方形标注的线段两端的最小项可以合并为A′E，三角形标注的线段两端的最小项可以合并为BE′，十字叉标注的线段两端的最小项可以合并为D′E′，双短线标注的线段两端的最小项可以合并为CE。最后得到

Y=A′E+BE′+D′E′+CE

(3)

(a)一变量 (b)二变量 (c)三变量

(d)四变量

(e)五变量图1 一到五变量最小项的立体图形

图2给出了使用卡诺图化简法得到的五变量卡诺图[5]。利用几何相邻关系，将第6、7列最小项合并为CE；利用左右两列闭合相邻关系，将第1、8列合并为D′E′；利用中心轴对称相邻关系，将两个正方形合并为A′E；利用左4列闭合相邻、右4列闭合相邻关系，将8个最小项合并为BE′。因此也得到与(3)式相同的结果。

对比图1(e)和图2可以看出，立体图形比卡诺图更能直观表现出逻辑相邻关系，方便找到所有可以合并的最小项，得到最简表达式。

图2 图1(e)立体图形对应的卡诺图

2 逻辑函数中的约束项和任意项

2.1 约束项

为了说明约束项的含义，以图3所示的交通信号灯电路为例。电路左侧有一个单刀三掷开关，与电源相连，开关状态受控制信号控制。电路右侧有红、黄、绿三盏交通信号灯，一端与地相连。开关与信号灯之间通过连接电路连接。A、B、C表示连接电路输入电平的高低，Y1、Y2、Y3表示连接电路输出电平的高低，1代表高电平，0代表低电平。

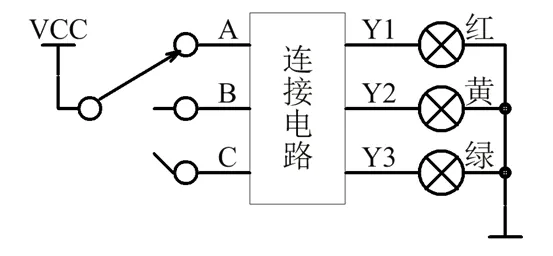
图3 约束项电路举例

当需要使红灯亮时，控制信号将开关拨到上边，使A=1，B=0，C=0，此时连接电路应当输出Y1=1，Y2=0，Y3=0，于是红灯亮，其它两盏灯熄灭。当需要使黄灯亮时，控制信号将开关拨到中间，使A=0，B=1，C=0，此时连接电路应当输出Y1=0，Y2=1，Y3=0，黄灯亮，其它两盏灯熄灭。当需要使绿灯亮时，控制信号将开关拨到下边，使A=0，B=0，C=1，此时连接电路应当输出Y1=0，Y2=0，Y3=1，绿灯亮，其它两盏灯熄灭。因此得到表1所示的连接电路真值表。

表1 图3中连接电路的真值表

A B CY1 Y2 Y31 0 01 0 00 1 00 1 00 0 10 0 1

由真值表得到输出变量的逻辑函数式：

(4)

从图3和表1看出，任何时刻A、B、C有且仅有一个为1，因此连接电路只有100、010、001三个输入值，而000、011、101、110、111五个输入值不会出现，这五个值对应的最小项A′B′C′、A′BC、AB′C、ABC′、ABC称为约束项。

因为使约束项为1的取值不可能出现，所以约束项恒等于0，即A′B′C′=0，A′BC=0，AB′C=0，ABC′=0，ABC=0，也可以表示为A′B′C′+A′BC+AB′C+ABC′=0。这就是约束项的逻辑函数式表示方法。

因为恒等于0的最小项加到任何逻辑函数上，都不会改变函数值，所以使用公式化简法时，可以根据需要任意添加约束项。例如，对图3连接电路输出变量Y1可以化简如下：

Y1=AB′C′=AB′C′+AB′C+ABC′+ABC=A

(5)

如果使用卡诺图化简法，约束项对应的方格可以与取值为1的方格一起合并，也可以不参与合并。当约束项参与合并时，就好像把它当成了1处理，相当于公式化简法里添加此约束项；不参与合并时，就好像把它当成了0处理，相当于公式化简法里不添加此约束项。所以约束项在卡诺图里既可以当作1，也可以当作0，根据化简需要决定是否参与合并。例如，图3连接电路输出变量Y2的卡诺图如图4所示，将右边两列的4个最小项(其中有3个约束项)合并，得到

Y2=B

(6)

同理，对Y3化简得到

Y3=C

(7)

综合式(5)～(7)可知，连接电路只需将A与Y1、B与Y2、C与Y3直接相连即可。

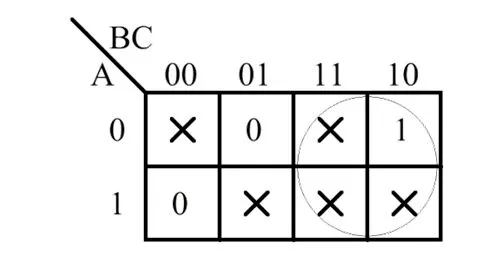
图4 图3中 的卡诺图

2.2 任意项

以图5所示交通信号灯电路为例，说明任意项的含义。电路左端有三个并联开关，与电源相连，开关状态受控制信号控制。电路右侧红、黄、绿三盏交通信号灯并联后，通过开关D接地。A、B、C、Y1、Y2、Y3的含义与图3相同。

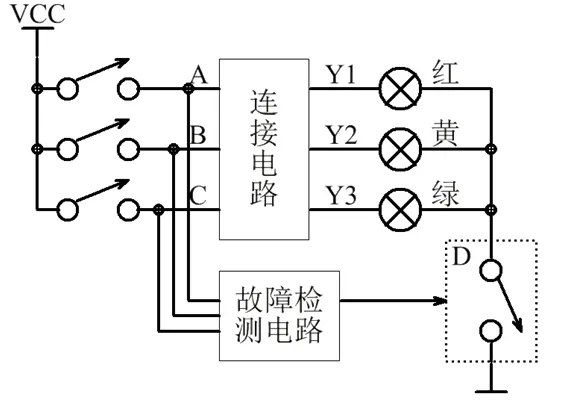
图5 任意项电路举例

当需要使红灯亮时，控制信号接通A左边的开关，断开B、C左边的开关，使A=1，B=0，C=0，此时连接电路应当输出Y1=1，Y2=0，Y3=0，使红灯亮，其它两盏灯熄灭。当需要使黄灯亮时，控制信号仅接通B左边的开关，使A=0，B=1，Y3=0，此时连接电路应当输出Y1=0，Y2=1，Y3=0，使黄灯亮，其它两盏灯熄灭。当需要使绿灯亮时，控制信号仅接通C左边的开关，使A=0，B=0，C=1，此时连接电路应当输出Y1=0，Y2=0，Y3=1，使绿灯亮，其它两盏灯熄灭。上面三种状态为正常状态，故障检测电路使开关D接通。

如果控制信号发生错误，A、B、C出现000、011、101、110、111这五个值时，故障检测电路则断开开关D。此时不管Y1、Y2、Y3为何值，三盏灯均熄灭，行人根据路面交通情况决定通行还是停止，从而避免信号灯显示错误信号，导致交通混乱的情况。这五个值对应的最小项A′B′C′、A′BC、AB′C、ABC′、ABC称为任意项。使任意项为1的取值可以出现，也可以不出现，不管是否出现，都不会影响电路功能。对于图5所示电路，任意项为1时，连接电路可以输出任意值。因此得到表2所示连接电路真值表。

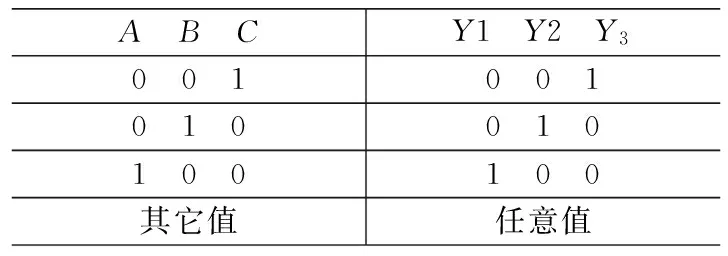
表2 图5中连接电路的真值表

因为任意项既可以等于1，也可以等于0。所以在使用公式化简法化时，可以根据需要添加任意项。使用卡诺图化简法时，任意项对应的方格可以与取值为1的方格一起合并，也可以不参与合并。因此任意项在化简时的处理方法与约束项完全一样。

由表2所示真值表得到Y1、Y2、Y3的函数式，再利用任意项进行化简，可以得到与式(5)～(7)相同的结果。因此，图5的连接电路也只需将A与Y1、B与Y2、C与Y3直接相连即可。

3 结语

本文用立体图形表示逻辑函数，虽然相对于卡诺图较为复杂，但逻辑相邻关系更直观，便于找出所有的逻辑相邻项，可以作为化简逻辑函数的一种参考方法。

本文以两个交通信号灯电路为例，分别解释了约束项、任意项的含义，以及它们的用法。虽然两者在函数化简时的处理方法相同，但含义不同。设计逻辑电路时，首先要对实际问题进行逻辑抽象，只有正确理解约束项和任意项的含义，才能准确表述逻辑问题。

[1] 闫石主编. 数字电子技术基础(第五版)[M]. 北京: 高等教育出版社, 2006.5

[2] W. J. Dally, R. C. Harting. Digital Design [M]. New York: Cambridge University Press, 2012

[3] 景亚霓. 浅谈逻辑函数中的任意项、约束项与无关项[J]. 石家庄: 教育教学论坛, 2014，37(9)：93-94

[4] 王选民. 数字电路中任意项、约束项、无关项的探讨[J]. 南京: 电工教学, 1995，17(2)：17-19

[5] 闫石,王红编. 数字电子技术基础(第五版)习题解答[M]. 北京: 高等教育出版社, 2006.10

Teaching Difficulties and Approach of the Logic Function Simplification

YANG Jing

(SchoolofElectronicInformation,WuhanUniversity,Wuhan430072,China)

Simplification of logic functions is a basic content of the Digital Logic Circuit course. It is found in actual teaching that the students often have difficulties in finding all the logic neighboring items of the Karnaugh maps, and understanding the text description of the bound items and arbitrary items. This paper uses three-dimensional geometry to represent the logic functions, which facilitates the validation of logic adjacent items. In addition, taking the traffic lights circuit as an example, this paper explains the meaning of the bound items and the arbitrary items.

logic function simplification; bound item; arbitrary item

2015-10-19;

2010-10-31

杨 静(1983-)，女，博士，讲师，主要从事电工基础理论教学、雷达系统和信号处理研究工作，E-mail：janeyang628@whu.edu.cn

G426

A

1008-0686(2016)05-0061-04