含随机风电出力及电网安全的电网调度策略研究
2016-03-02罗亦梅
罗亦梅,张 里,吴 琛,郝 珑
含随机风电出力及电网安全的电网调度策略研究
罗亦梅1,张里2,吴琛3,郝珑4
0引言
中国“十二五”规划实施以来,作为一种绿色、清洁的可再生能源,风电在中国北部和沿海地区迅速发展。大型风电场的并网运行是目前中国利用风能的主要模式,也是智能电网发展的重要组成部分[1]。大规模的风电并网不仅缓解电力供应紧张的形式,同时也减少了能源利用过程中大量温室气体的排放[2-3]。
风电与传统的火电机组和水电机组相比,具有强烈的波动性和随机性,其并网运行给电力系统调度带来新的问题和挑战[4-5]。针对风电功率不确定性的经济调度问题,目前国内外的一些学者进行了大量的研究。文献[6]通过应用机会约束规划模拟风电功率的随机波动特性,建立了考虑机组组合的含风电场电力系统经济调度模型;文献[7]提出节能发电调度发电计划的编制算法,首先根据优先顺序法确定火电机组开机方法,然后采用等微增率进行功率分配;文献[8]提出在经济调度的目标函数中计及高估和低估风电的经济代价,较合理地刻画了风电功率的概率分布特性,具有一定的工程实用性;文献[9]为应对风电功率预测误差给系统调度带来的影响,在ED模型中同时考虑系统正、负旋转备用容量约束;文献[10]应用模糊集理论建立了含风电场经济调度的模糊模型;文献[11]构建含风电场环境经济调度的随机优化模型,将燃煤机组的发电成本最小和污染气体排放量最小同时最为目标函数进行优化。
上述发电调度模型中并未考虑随机风电出力,以及输电元件传输容量的约束。在传统经济调度模型中考虑了网络安全约束,并将风速的概率模型和风机出力相结合,通过分段函数表达风电场出力的概率分布函数,利用风电场出力的分布函数对模型进行确定性转化,使得仿真结果更接近实际情况。最后利用量子行为粒子群算法对模型进行求解,同时对调度模型进行敏感性分析。
1风电出力的概率模型
通过长期实测数据统计和拟合分析,普遍认为二参数的威布尔分布能够较好描述风速v的随机分布规律[12]。分布函数为
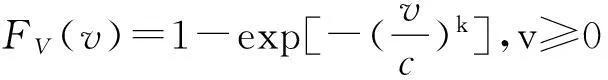
(1)
式中:k为形状参数;c为威布尔分布的尺度参数。根据其分布函数可得威布尔分布的概率密度函数为

(2)
由于影响风能输入和功率输出之间关系的因素很多,所以无法在建模中一一分析。研究人员使用通用、简化的模型[13]来描述风速和输出功率的关系。

(3)
式中:W为风电实际出力;V为实际风速;wr为风电场的额定容量;vin、vr、vout分别为风电机的切入风速、额定风速和切除风速。
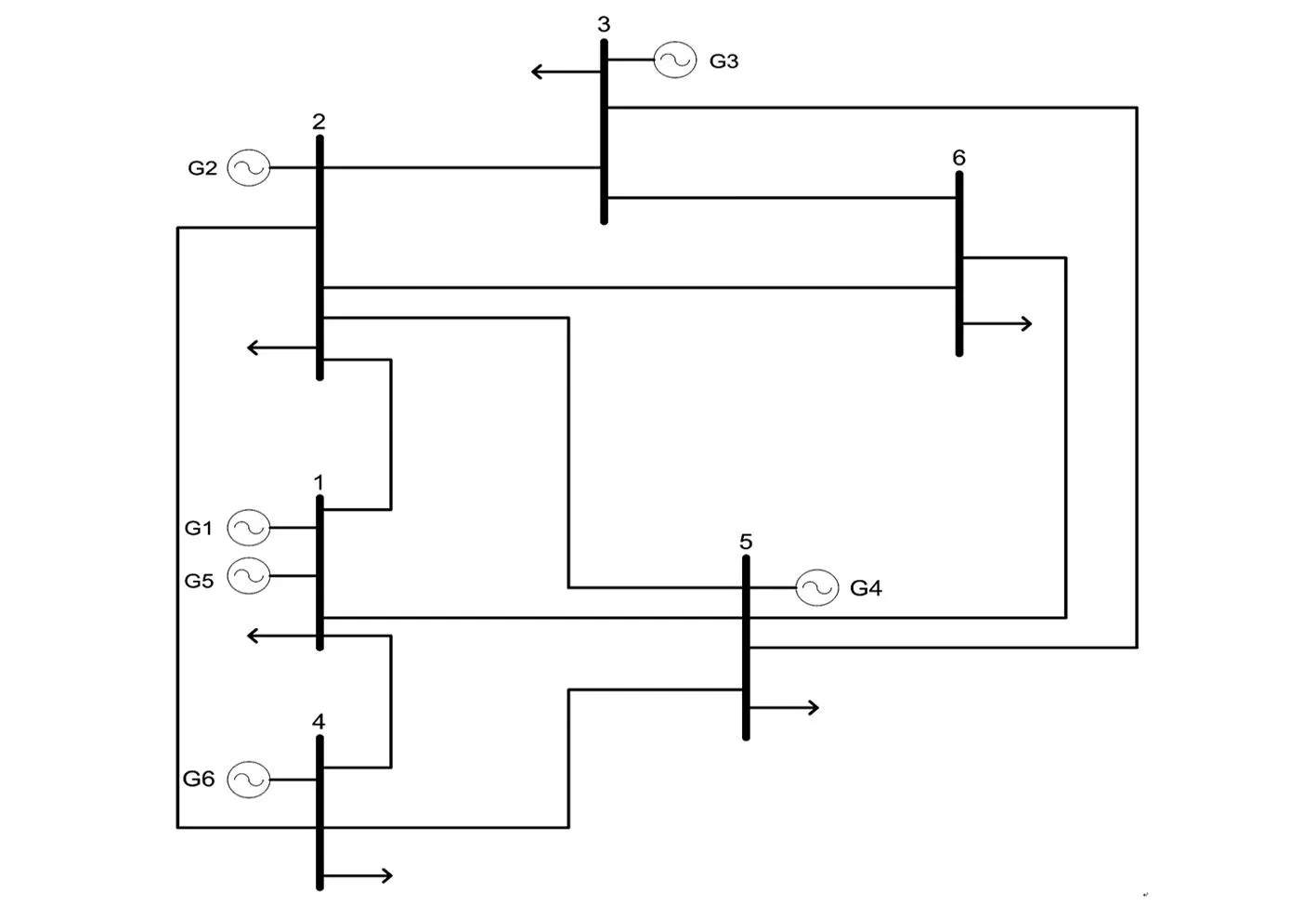
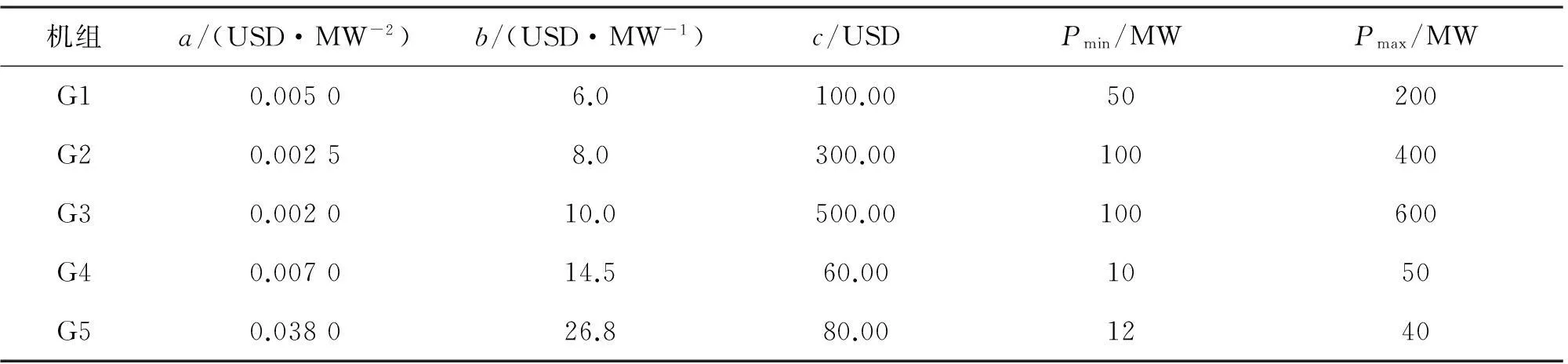
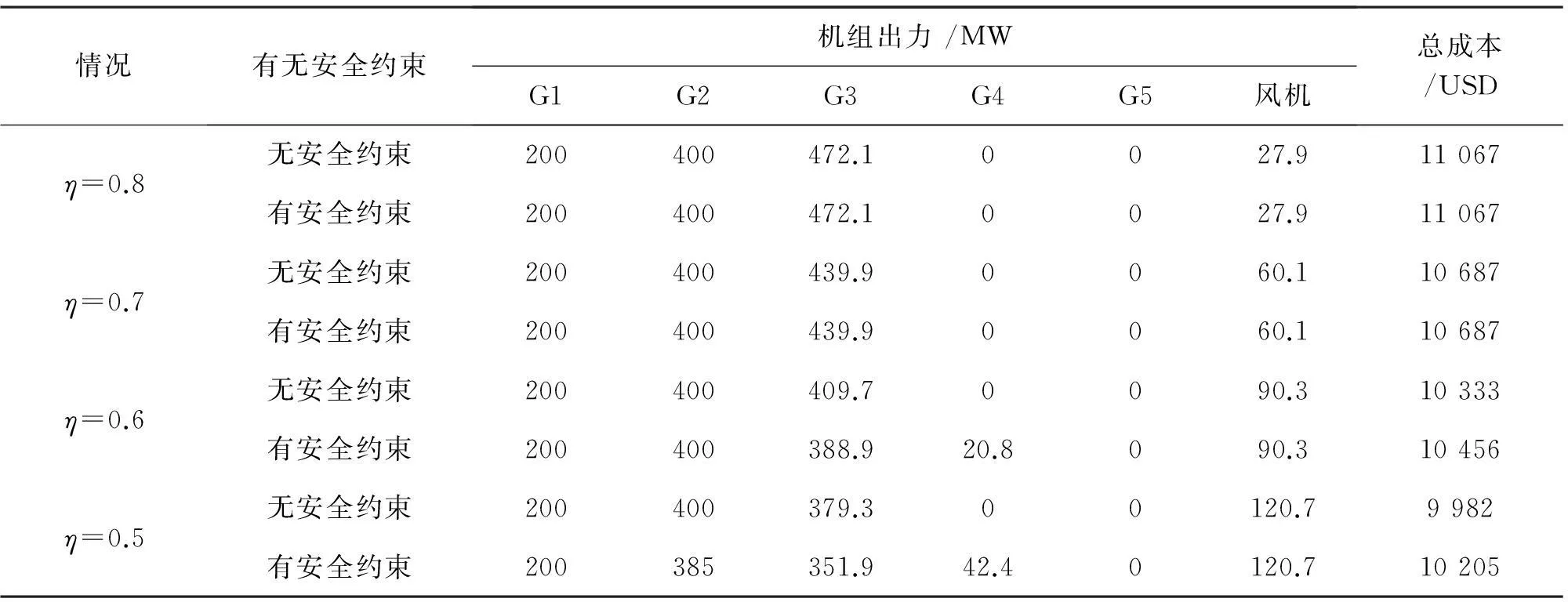
在经济调度中将采用以上模型,根据随机变量函数的分布[14]可知,vin≤V (4) 式中,h=(vr/vin)-1。在计算分布函数时需要采用分段线性化。 p(W=0)=p(V (5) 式中,p为概率。 P(W=wr)=P(vr≤V (6) 为求取连续部分的概率分布,对式(4)积分为 (7) 此外, P(W>wr)=0 (8) 综合式(5)~式(8),得到W的概率分布函数为 FW(w)=P(W≤w)= (9) 2电力系统安全经济调度 发电成本为 (10) 式中:N为系统内燃煤机组数;Pi为燃煤机组i的有功出力;FC为燃煤机组的总成本。 1)功率平衡约束 (11) 式中:PD为系统负荷需求;Ω(PW)为风电场出力PW的函数。由于PW为随机变量,因此可将式(11)以概率的形式描述为 (12) 式中,η为满足负荷需求的置信水平。 2)机组出力约束 燃煤机组的出力约束为 Pimin≤Pi≤Pimax (13) 风电场的出力约束为 0≤PW≤PWmax (14) 3)网络安全约束 -PL≤BdiagLB-1[Pg-PD]≤PL (15) (16) 式中:B为系统的导纳矩阵;xi为支路i的电抗;Nl为系统支路条数;L为系统支路节点的连接矩阵;PL为支路功率约束向量。 求解机会约束规划问题的一种常用的方法是将其转化为确定性优化模型。式(12)可转化为 (17) 整理后: (18) 3求解算法 含随机风电出力及电网安全的电网经济调度模型是一个多变量、非线性、混合整数规划问题。在Matlab平台上利用量子行为粒子群算法[16-17]求解计及网络安全约束时的电力系统经济调度模型,该算法具有全局收敛性、控制参数更少,收敛速度更快、寻优能力强等优点。 在粒子群中引入一个平均最好位置C(t)来计算粒子下一步迭代的变量,定义为所有粒子个体最好位置的平均,即 (19) 式中:M为粒子的个数;Pi为粒子i的局部最好位置。于是粒子的迭代方程变为 x(t+1)=p±λ×|Cj(t)-x(t)|×ln[1/u] (20) 式中:u=rand(0,1);λ称为收缩-扩张系数,调节它可以控制算法的收敛速度。这里λ取值为 λ=(1-0.5)×(Maxiter-t)/Maxiter+0.5 (21) 式中:Maxiter为最大迭代次数;t为当前迭代次数。式(19)~式(21)称为具有量子行为粒子群算法。 根据数学模型,采用基于随机模拟的量子行为粒子群算法流程如下: 1) 读取系统数据,如输入负荷、火电机组参数、线路参数和风电出力的预测值等。再次是输入量子行为粒子群算法参数,如最大迭代次数、粒子群大小。 2) 种群初始化。随机生成各时段各火电机组有功功率和备用容量,组成一个个体,根据式(11)~式(16)检验个体的可行性;若个体不可行,则重新生成个体,直至初始群体生成完毕。 3) 首先根据式(19)计算粒子群的平均最好位置,计算粒子当前位置的适应值。 4) 粒子位置的更新。根据式(20)对每个粒子的位置进行更新,同时验证是否越限,如果越限则需要重新更新粒子。然后计算每个粒子的适应值,如果优于当前粒子个体极值,则更新个体极值。如果所有粒子的个体极值有优于当前的全局极值,则更新全局最优。 5) 判断是否达到迭代次数。如果未达到则返回步骤3)、步骤4);否则输出最好的粒子作为最优解。 4算例分析 利用文献[15]中含有5台燃煤机组和1个风电场系统进行仿真计算。系统接线图见图1,燃煤机组的发电成本系数和机组出力限制见表1,线路参数和负荷分布参数见表2及表3。系统负荷为1 100 MW。网络约束在这里只考虑线路的传输容量约束。在编程求解模型时,粒子群个数设置为40个,迭代运行次数为500。 图1 仿真系统接线 机组a/(USD·MW-2)b/(USD·MW-1)c/USDPmin/MWPmax/MWG10.00506.0100.0050200G20.00258.0300.00100400G30.002010.0500.00100600G40.007014.560.001050G50.038026.880.001240 表2 线路参数 表3 节点负荷分布 表4 风电场参数 表5 不同置信水平η下的机组出力 风电场参数见表4,威布尔分布的参数k=2,c=12 m/s。 4.2.1在是否计及网络安全约束下,不同置信水平对机组出力的影响 取形状参数k=2,尺度参数c=12 m/s。分别对置信水平η为0.8、0.7、0.6和0.5下进行计算,表5给出了是否计及网络安全约束下的机组出力。 对计算结果进行分析可知,随着满足负荷需求置信水平η的下降,系统接入的风电场出力增加,燃煤机组出力下降,同时燃煤机组发电成本降低。在不考虑网络约束情况下,最小发电成本由11 067 $/h降至9 982 $/h;而考虑网络安全约束情况下,最小发电成本由11 067 $/h降至10 205 $/h。 同时针对相同的置信水平,考虑网络安全约束比不考虑网络安全约束所需燃煤机组成本高。这说明随着置信水平的降低,系统接入的风电场出力增加,并同时伴随着部分线路潮流越线的情况,考虑网络安全约束后成本增加的本质是由发电成本高的机组代替发电成本低的机组出力,从而满足电网处于安全运行状态。 4.2.2在计及网络安全约束下,不同负荷对机组出力的影响 取形状参数k=2,尺度参数c=12 m/s。置信水平η为0.6,取负荷分别为1 000 MW、1 100 MW和1 200 MW进行优化。表6给出了不同负荷下的调度结果。 表6 不同负荷下的机组出力 对计算结果进行分析,在相同的置信水平下,风电场出力为不变量。随着负荷的增加,未达到最大出力的机组会增加出力,同时所需成本也会相应增加。 4.2.3在计及网络安全约束下,不同尺度参数对机组出力的影响 取形状参数k=2,置信水平η为0.6,分别取尺度参数为12 m/s、15 m/s、18 m/s和21 m/s进行优化。表7给出了发电成本最少的调度结果。 表7 不同尺度参数下的机组出力 对计算结果进行分析可知,尺度参数从12 m/s增加到21 m/s,风电场出力从90.3 MW增加到145.6 MW,从而降低了燃煤机组的成本。结果显示,尺度参数反映了风电场的平均风速,因此随着尺度参数的增加风电场的出力增加,但是增幅却在减少,同时伴随着发电成本在逐渐降低。 4.2.4在计及网络安全约束下,不同形状参数对机组出力的影响 取置信水平η=0.6,尺度参数c=12 m/s。在计及网络安全约束下,分别计算形状参数k=1.8、2.0、2.2和2.4下的燃煤机组和风电场调度结果。 表8 不同形状参数的机组出力 比较计算结果可知,随着形状参数增加,系统风电场出力从82.4 MW增加到101.5 MW,同时燃煤机组总出力减小,最小发电成本由10 520 $/h下降至10 370 $/h。 图2 不同形状参数k下的风速概率密度函数 从图2可知,随着k值增加,风速概率密度函数曲线逐渐变陡,且密度函数的峰值逐渐增加,同时出现概率峰值对应的风速值也逐渐增大,但增加幅度变小。这表明,随着k值增加,风速分布更接近于风速峰值附近,概率峰值对应的风速值也增加,风电场的出力增加。 5结论 1) 建立了含随机风电出力和电网安全的电网经济调度模型,并利用风电出力的分布函数将风电不确定性转化为确定性模型; 2) 在考虑网络安全约束时,为了使电网安全运行,部分机组出力结果的变化导致系统成本增加; 3) 分析了在考虑网络安全约束下,对调度模型进行敏感性分析; 4) 仿真结果表明了所提调度方法的合理性和有效性,为含随机风电出力和电网安全的电网经济调度提供参考。 参考文献 [1] 王淑娟,郭元. 我国大规模发展风电的机制设计[J]. 太阳能学报,2001,22 (1): 59-63. [2]Denny E. Wind Generation, Power System Operation, and Emissions Reduction [J]. IEEE Transaction on Power Systems,2006,21(1): 341-347. [3]王睿,张粒子,张丽娟,等. 含风电场系统风电与抽水蓄能匹配容量研究[J]. 太阳能学报,2012,33(6): 1039-1043. [4]J. Wang, A. Botterud, R. Bessa. Wind Power Forecasting Uncertainty and Unit Commitment [J]. Applied Energy,2011,88(11): 4014-4023. [5]K. Methaprayoon, W. J. Lee. An Integration of ANN Wind Power Estimation into UC Considering the Forecasting Uncertainty [C]. Industrial and Commercial Power Systems Technical Conference,2005. [6]孙元章,吴俊,李国杰,等. 基于风速测量和随机规划的含风电场电力系统动态经济调度[J].中国电机工程学报,2009,92(4): 41-47. [7]施建华,谭素梅.节能发电调度发电计划编制算法[J].电力系统自动化,2008,32(24): 48-51. [8]董晓天,严正,冯冬涵,等. 计及风电出力惩罚成本的电力系统经济调度[J]. 电网技术,2012,36(8): 76-80. [9]周玮,彭昱,孙辉,等. 含风电场的电力系统动态经济调度[J]. 中国电机工程学报,2009,29(25): 13-18. [10]陈海焱,陈金富,段献忠. 含风电场电力系统经济调度的模糊建模及优化算法[J]. 电力系统自动化,2006,30(2): 22-26. [11]邱威,张建华,刘念. 含大型风电场的环境经济调度模型和解法[J]. 中国电机工程学报,2011,31(19): 8-16. [12]王成山,郑海峰,谢莹华,等. 计及分布式发电的配电系统随机潮流计算[J]. 电力系统自动化,2005,29(24): 39-44. [13]雷亚洲,王伟胜,印永华,等. 风电对电力系统运行的价值分析[J], 电网技术,2002,26(5):10-14. [14]Stiebler M.风力发电系统[M]. 北京:机械工业出版社,2010: 10-17. [15]Wood Allen J, Wollenberg Bruce F. Power Generation, Operation and Control[M]. New York: John Wiley & Sons Inc, 1996. [16]S.N. Omkar, G.Narayana Naik. Quantum Behaved P- article Swarm Optimization for Multi-objective Design Optimization of Composite Structures [J]. Expert System with Application, 2009, 36(8): 11312-11322. [17]Yejie Cai, Jun Sun. Optimizing the Codon Usage of Sy- nthetic Gene with QPSO Algorithm [J]. Journal of Theoretical Biology, 2008, 254 (1): 123-127. 张里(1984),博士研究生,从事风力发电方面研究。 (1.成都理工大学核技术与自动化工程学院, 四川 成都610059; 2. 国网四川省电力公司技能培训中心,四川 成都610072; 3. 国网重庆市电力公司检修分公司,重庆400039; 4. 国网保定供电公司,河北 保定071000) 摘要:随着风电基地在中国北部和沿海地区大力建设,风电在电网中的比例不断提高,这对电力系统的经济调度运行提出新的考验。特别是风电的间歇性和波动性使得经济调度具有更多不确定性。将风速的概率模型和风机出力相结合,利用风电场出力的概率分布函数将风电场出力的随机模型转化为确定性模型,构建以机组的发电成本最小为目标函数,同时计及电网网络安全约束。在优化算法上,利用量子行为粒子群算法对模型进行求解,最后对调度模型进行敏感性分析。仿真结果表明,所提模型和方法是可行、有效的,具有一定的实用价值。 关键词:风力发电;经济调度;网络安全约束;置信水平 ;量子行为粒子群算法 Abstract:Wind generation has attracted great attention with the increase of the capacity of large wind farms connected to power grid, thus it brings new challenges to economic dispatch of traditional power system. Especially, more uncertainties in economic dispatch are produced by the random variation of wind power output. The wind velocity probability model is combined with wind generator output, and the probability distribution function of wind power output is expressed by piecewise function. According to the cumulative distribution function of wind power, the stochastic optimization problem is transformed to a deterministic one. Minimizing the fuel cost of thermal generators is taken as objective functions, at the same time, the network security constraints are considered. Finally, the effect of different load, shape parameter and scale factor of the scheduling results are considered too. The effectiveness of the proposed method is verified by the results of calculation examples. Key words:wind power; economic dispatch; network security constraint; confidence level; quantum behaved particle swarm optimization (收稿日期:2015-11-02) 作者简介: 基金项目:国家自然科学基金项目(50977059);国家电网公司科技项目——大规模风电并网调度运行支撑关键技术研究与应用 中图分类号:TM73 文献标志码:A 文章编号:1003-6954(2016)01-0006-06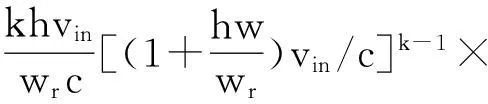
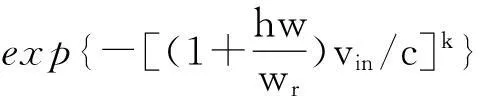
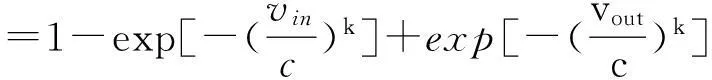




2.1 目标函数

2.2 约束条件
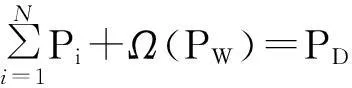
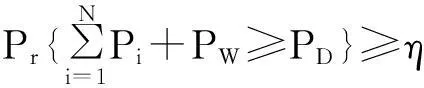
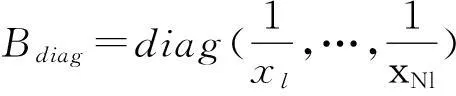
2.3 模型的确定性转化
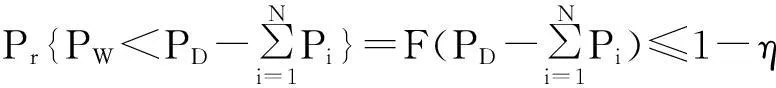


3.1 量子行为粒子群算法

3.2 算法流程
4.1 算例描述




4.2 算例验证