基于小鼠大脑MRM图像灰度分布的个体结构网络构建的研究
2016-03-02付振荣林岚张柏雯吴水才
付振荣,林岚,张柏雯,吴水才
北京工业大学 生命科学与生物工程学院,北京 100124
基于小鼠大脑MRM图像灰度分布的个体结构网络构建的研究
付振荣,林岚,张柏雯,吴水才
北京工业大学 生命科学与生物工程学院,北京 100124
结构磁共振成像脑网络分析技术结合了sMRI成像、医学图像处理、复杂网络及图论分析等技术方法,通过对大脑不同感兴趣区之间的特征关系进行分析,能够更好地分析脑组织结构之间的关系及与疾病的关联性等。目前,基于人脑sMRI的大脑灰质结构网络已成为脑网络研究的一个热点,但是基于小鼠MRM的大脑灰质网络分析还相对较少。本文首先通过构建基于KL散度的小鼠MRM个体灰质脑网络,并在此基础上进行网络拓扑属性的分析,该方法可以应用于脑老化和因疾病带来的小鼠脑网络变化的研究。
小鼠大脑;个体脑网络;KL散度
近年来,随着神经影像数据采集设备和技术的快速进步,研究者们逐渐将复杂网络的相关理论应用到大脑研究之中,脑网络分析也随之成为神经影像学领域的研究热点[1-3]。基于弥散张量成像(Diffusion Tensor Imaging,DTI)[4]、功能性磁共振成像(Functional Magnetic Resonance Imaging,fMRI)[5]、结构磁共振成像(Structure Magnetic Resource Imaging,sMRI)[6]、脑电图(Electroencephalo-Graph,EEG)[7]和脑磁图(Magnetoencephalogram,MEG)[8]等脑成像技术被用于构建复杂脑网络。通过对复杂网络拓扑属性的分析,可以在一定程度上帮助研究者了解大脑结构与功能之间的相互关系[9],揭示大脑传递信息与处理信息的运行机理,还能够用于大脑年龄预测[10-11]以及疾病的诊断和预测[12-14]等研究。
由于sMRI易获取、包含脑区间的结构连接信息等优势,基于它的结构网络也越来越受到研究者们的重视。脑网络构建主要包含两个部分,即节点的定义和节点间的连接强度(边)的定义。Gene等[15]依据大脑中不同脑区间存在协同变化的原理,采用一种改良的主成分分析方法(Scaled Subprof le Model,SSM),得到了反映载脂蛋白ApoE ε4等位基因携带者的结构特征网络。此方法可以用来衡量不同个体对该结构特征网络的表示程度,但此方法无法通过图论进行复杂网络分析。He等[16]通过将对象分组大脑分区,计算不同组对象各个脑区间的相关性得到全脑的相关性矩阵,并进一步通过图论分析发现该网络具有小世界特征和无标度性。该方法虽能够采用不同的结构特征构建网络,但只能基于一组数据构建一个平均脑网络。由于该方法构建的是一组的平均脑网络,对数据量要求较大。同时,平均网络是基于一组对象的平均特征,无法准确反应个体对象间的差异。针对平均网络的不足之处,研究人员提出了构建个体网络的新方法。Tijms等[17]将大脑定义为6982个立方体的脑区节点,各个节点内部包含的27个体素可以组成特征向量,通过计算这些特征向量间的相关性可以得到脑区连接的强度。该方法可以构建个体对象的结构网络,但立方体大小和其中的旋转操作存在一定的任意性。Kong等[18]提出了基于KL散度(Kullback-Leibler_divergence)得到KL散度相似性度量(Kullback-Leibler_divergence Similarity,KLS)构建大脑个体灰质网络的方法。KL散度能够间接反映不同感兴趣区之间的相似度,通过计算不同脑区间特征的概率密度分布得到不同脑区之间的KL散度。
动物模型在医学领域的研究中有着不可替代的作用。与人类相比,动物模型具有可操作性强、生命周期短、以及能够批量生产等优势,能够帮助科研人员加快研究进度以及更全面的认识疾病等研究内容的本质。随着高分辨率影像技术的快速发展,能够采集小动物大脑图像的磁共振显微成像技术(Magnetic Resource Microscopy,MRM)[19]为利用动物模型进行神经影像的研究提供了技术支持。MRM技术不仅能够采集高分辨率的小鼠活体三维图像,而且避免了组织切片中的空间变形。基于MRM 的小鼠脑图像分析的发展吸引了不少研究人员的关注[20]。
目前,基于人脑sMRI的灰质结构网络的研究正处于高速发展阶段[21-22],但基于动物模型构建结构脑网络的研究还相对较少。人脑和鼠脑无论是在形态还是体积上都存在非常大的差异,例如,鼠脑的体积一般仅为人脑的三千分之一,并且鼠脑的表面较光滑,没有复杂的脑沟与脑回。本文将KL散度的脑网络构建进一步从人脑延伸到了小鼠脑MRM之中。本研究主要基于小鼠的T2 MRM影像展开。T2 MRM影像反映的是组织的横向磁化强度Mxy衰减的快慢。不同脑区间的图像灰度分布的不同,反映了不同脑区间横向弛豫时间的差异。而这种差异在一定程度上可以反映不同脑区间组织特征的差异性(如神经元细胞的种类、神经元细胞的密度等)。本文基于小鼠不同脑区间的KLS建立小鼠大脑的个体灰质网络,并通过进一步分析网络的拓扑属性,验证这种方法在小鼠MRM个体脑网络构建中的适用性及延展性。
1 数据采集
本次研究采用的数据来自于新加坡国立大学(Computational Functional Anatomy Lab)的小鼠影像数据库(http://www.bioeng.nus.edu.sg/cfa/mouse_atlas.html)。该数据库包含5只雄性C57BL/6小鼠T2 MRM 影像。图像采用德国布鲁克7-T/20-cm ClinScan MRI进行采集,其中扫描序列为3DT2加权快速自旋回波(重复时间/回波时间=2000 ms/46 ms,视野范围=9 mm×13 mm×25 mm,体素尺度= 100×98×98 micron),采集时间为1小时23分[23]。由于7-T磁场会给图像带来较强的不均匀性[24-25],数据库中的MRM图像都采用N3(Nonparametric Non-uniform Intensity Normalization)[26]进行非均匀场校正,并且灰度被标准化到0~255。数据库中小鼠图像均被手工分割为39个感兴趣区。脑区划分流程为,首先将图像刚体配准到Franklin and Paxinos小鼠脑图谱空间中[27-28],再将MRM图像进行手工分割。图谱划分原则为:首先将容易分辨的脑区划分出来,然后再将不易识别、轮廓不清晰的脑区严格按照组织切片图谱来进行划分,在很大程度上保持了脑区划分的准确性。由于在脑网络分析中,只需要大脑灰质和神经核团。本研究利用已分割的小鼠大脑个体脑区图谱去除14个相关脑区,其分别属于脑白质、脑脊液、小脑和脑干等部分。然后,剩余的25个脑区被用于脑网络构建。25个灰质脑区详细定义见表1。
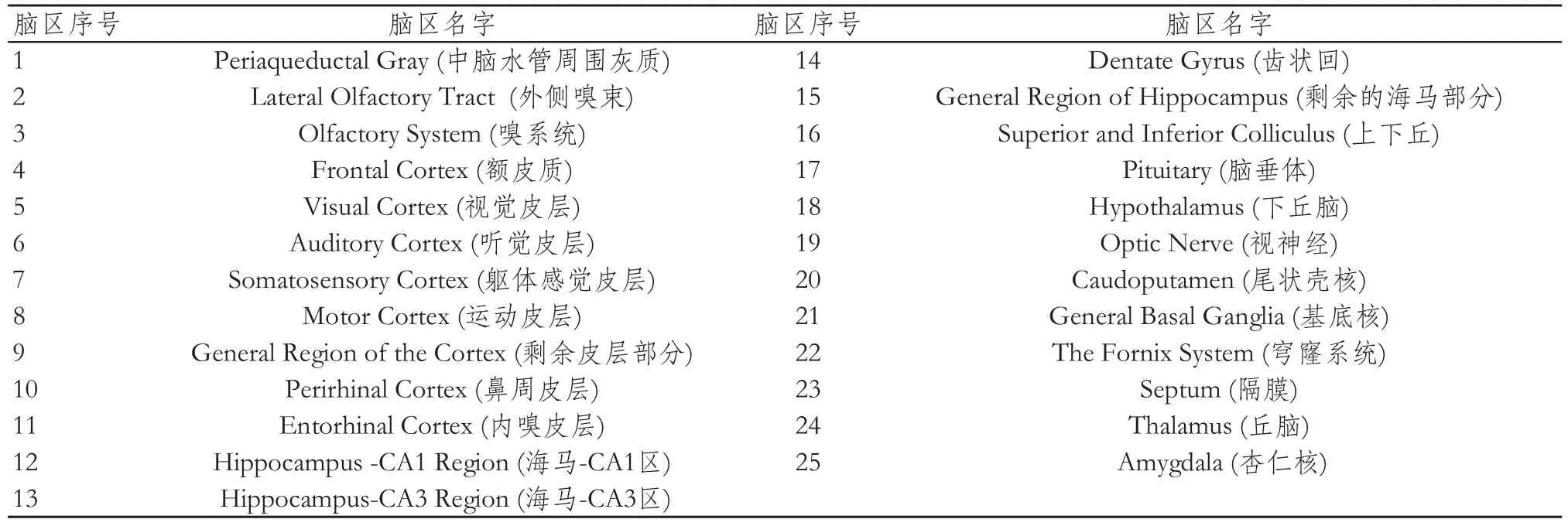
表1 小鼠脑区对照表
2 方法及结果
本研究构建了两种类型的脑网络:一种为基于小鼠脑T2 MRM图像构建的灰质个体网络;另一种为将小鼠脑T2 MRM进行高斯平滑处理 (FWHM为4个体素)后所构建的网络。两种方法网络构建的流程基本一致,详见图1。

图1 基于小鼠脑T2 MRM图像的个体灰质网络构建流程图
该流程主要分为以下3个步骤:
(1)基于已有的小鼠脑个体感兴趣区分区对小鼠脑MRM图像进行分割。
(2)计算各个感兴趣区的灰度概率密度分布,得到反映两两感兴趣区相关关系的KLS相关性矩阵。
(3)基于KLS相关性矩阵构建网络,并进行复杂网络计算与分析。
2.1 网络节点及边
在基于脑区水平的大尺度的脑网络构建中,定义网络节点和网络连接(边)是最关键的两步。本文中25个感兴趣区被定义为大脑结构网络的节点。MRM影像中的灰度差异反映了小鼠不同脑组织间的T2值的差异。这里我们通过基于KL散度的相似性度量KLS来计算两个脑区之间的图像灰度概率密度分布的相关性。KL散度为一种通用的可以计算两个概率密度分布相似度的度量方法。其中,各个脑区的灰度密度分布通过核密度估计(Kernel Density Estimation,KDE)来进行计算(http://cn.mathworks.com/matlabcentral/fileexchange/14034-kernel-density-estimator?Requested Domain = www.mathworks.com)。由于数据库中的小鼠图像的灰度已经被标准化到0~255之间,这里将KDE的采样点个数定为256个。在得到每个脑区的灰度概率密度分布之后,计算各个脑区间的KL散度,然后再通过KL散度来计算KLS,即得到相关性矩阵。KLS的范围为0到1,1表示两个脑区具有完全相同的灰度概率密度分布,而0表示两个脑区的灰度概率密度分布不存在任何交集。KL距离的计算公式为:

其中n为灰度分布中样本点的个数,P和Q代表不同脑区的灰度分布。由于DISKL(P||Q)和DISKL(Q||P)不是等值的,我们用对称的方法来消除这种不等值带来的误差,即将DISKL(P||Q)与DISKL(Q||P)相加得到一个新的KL距离。

最后,KLS的计算公式为:
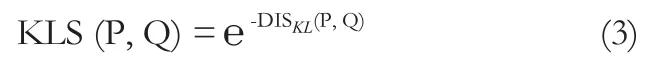
2.2 网络分析
基 于MATLAB的GRETNA 工 具 包(http://www.nitrc.org/projects/gretna/)[29]被 用 来 进 行复 杂 网 络 分 析。GRENTA是 北 京 师 范 大 学 开发的具有图形化界面的能够进行网络分析的工具箱。本文中的主要网络指标[30]包括:聚类系数(clustering coeff cient,Cp)、标准化聚类系数(标准化Cp)、最短路径长度(Characteristic Pathlength,Lp)、标准化最短路径长度(标准化Lp)、全局效率(global eff ciency,Eglob)、标准化全局效率(标准化Eglob)、局部效率(local eff ciency,Eloc)和标准化局部效率(标准化Eloc)和网络中心节点。随机网络的构建是通过拓扑重新布线算法(Topological rewiring Algorithm)[31]产生100个与真实网络具有一致的节点数、边数和度分布的随机网络。此外,笔者还计算了以上各个参数在所定义的稀疏度范围内的积分,即曲线下面积(Area Under Curve, AUC):聚类系数AUC(aCp)、最短路径长度AUC(aLp)、全局效率AUC(aEglob)、局部效率AUC(aEloc)及其相应的标准化参数。这些参数值使得我们可以独立于具体稀疏度阈值来分析网络拓扑属性。每个加权连接矩阵中的相关系数都需要取特定的阈值进行二值化,二值化网络保留了相关系数中相对较大的连接。目前尚无确定的方法来选择一个唯一的稀疏度,因此我们将稀疏度范围定为0.15~0.4,每隔1%选取一个稀疏度。
2.3 结果分析
图2为小鼠脑MRM图像和平滑后的MRM图像,通过KLS计算生成的平均相关性矩阵,其中二值化网络的网络稀疏度为20%。图2中的左图为平均加权相关性矩阵,相对未平滑的图像,经过平滑处理后的图像各脑区间具有更强的相关性。经过平滑运算,每个脑区和它相临近的脑区间的相关性都会得到提升,具体表现为脑区相关性的整体提高。由于平滑处理对各个脑区边缘的灰度分布影响更大,因此它对于各个脑区的影响是不一致的。一般脑区体积越小,与周边其它脑区的灰度分布差异越大,平滑操作的影响也就越大。图2中的右图为二值化矩阵,平滑前后,网络的整体拓扑结构有了较大的变化。
小世界网络是介于随机网络和规则网络之间[32-34]的一种网络。小世界网络具有较短的最短路径长度和较大的聚类系数这两个重要的特点。聚类系数越大的网络,局部效率就会越高;最短路径长度越长,全局效率就会越低。规则网络的聚类系数较高,但是最短路径长度较长;随机网络的聚类系数较低,但最短路径长度较短。小世界网络作为这两种网络的中间产物,具有比规则网络高的聚类系数,以及比随机网络低的最短路径长度。脑网络如果是小世界网络,与随机网络相比,应具有更高的聚类系数值与局部效率(标准化 Cp>1,标准化 Eloc >1),同时具有相近的最短路径长度和全局效率(标准化 Lp~1 ,标准化 Eglob~1)。图3为两种不同处理流程(数据库中MRM图像与平滑后图像)处理后,标准化的脑网络参数在不同稀疏度下的分布图。对于未平滑处理的图像生成的网络,标准化Cp的值随稀疏度的增大呈下降趋势,标准化Cp的最大值为5.78,最小值为1.40,总体均值为2.27,标准差为0.78,小鼠结构脑网络与随机网络相比具有较高聚类系数;标准化 Eloc的值随稀疏度的增大呈下降趋势,标准化 Eloc 的最大值为5.75,最小值为1.12,总体均值为1.90,标准差为0.79,小鼠结构脑网络与随机网络相比具有较高的局部效率;标准化Lp的值随稀疏度的增大呈缓慢下降趋势,趋向于1,标准化Lp的最大值为2.47,最小值为1.10,总体均值为1.29,标准差为0.24,小鼠结构脑网络与随机网络相比最短路径长度相近;标准化Eg的值随稀疏度的增大呈缓慢上升趋势,趋向于1,标准化Eg的最大值为0.92,最小值为0.40,总体均值为0.79,标准差为0.11,小鼠结构脑网络与随机网络相比全局效率相近。对于平滑后图像生成的网络,标准化Cp的值随稀疏度的增大呈下降趋势,标准化Cp的最大值为4.41,最小值为1.48,总体均值为2.52,标准差为0.79;标准化 Eloc的值随稀疏度的增大呈下降趋势,标准化 Eloc的最大值为4.31,最小值为1.22,总体均值为2.06,标准差为0.83;标准化Lp的值随稀疏度的增大呈缓慢下降趋势,标准化Lp的最大值为1.92,最小值为1.07,总体均值为1.29,标准差为0.26;标准化Eg的值随稀疏度的增大呈缓慢上升趋势,标准化Eg的最大值为0.94,最小值为0.52,总体平均值为0.80,标准差为0.13。该网络与随机网络相比,具有较高聚类系数、局部效率和相近的最短路径长度与全局效率。两种网络均满足小世界属性。

图 2 平均相关性矩阵示意图
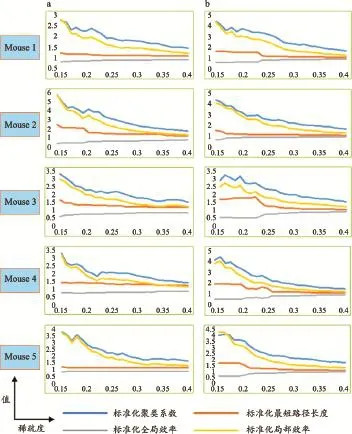
图3标准化脑网络参数分布图
图4为基于AUC值的各个样本的全局网络参数示意图。五只不同小鼠个体网络的聚类系数AUC的均值为0.13,标准差为0.02;最短路径长度AUC的均值为0.72,标准差为0.12;标准化聚类系数AUC的均值为0.56,标准差为0.12;标准化最短路径长度AUC的均值为0.32,标准差为0.05,全局效率AUC的均值为0.09,标准差为0.02、局部效率AUC的均值为0.15,标准差为0.02,标准化全局效率AUC的均值为0.20,标准差为0.02;标准化局部效率AUC的均值为0.47,标准差为0.09。对于平滑后图像生成的网络参数,五个不同小鼠个体网络的聚类系数AUC的均值为0.17,标准差为0.01;最短路径长度AUC的均值为0.62,标准差为0.06;标准化聚类系数AUC的均值为0.63,标准差为0.02;标准化最短路径长度AUC的均值为0.32,标准差为0.02、全局效率AUC的均值为0.11,标准差为0.01;局部效率AUC的均值为0.19,标准差为0.004、标准化全局效率AUC的均值为0.20,标准差为0.01;标准化局部效率AUC的均值为0.51,标准差为0.04。不同小鼠的网络参数的AUC值在平滑后个体差异性减少。
网络中的hub节点是网络通讯中重要的中心节点,定义hub节点的方法有很多,比如度、中介性指标等。我们前期的研究发现这些定义指标间具有很强的相关性[35],因此这里采用中介性指标来定义Hub。首先计算中介性指标在25个脑区的平均值,各个脑区中介性指标的大小反映了该脑区节点在网络中的重要性。然后根据以下公式计算各个小鼠个体脑区节点重要性的相似度和特异性。

m和n为小鼠的编号,N为小鼠个体的总数,Bdm与Bdn为整体网络稀疏度范围内的平均节点中介性指标。图5为5只小鼠的个体网络脑区节点中介性指标的相似度与特异性的平均值与标准差。不同个体的脑区节点中介性指标具有较大的特异性,相似度较低。平滑处理可以提高相似度,降低它们之间的特异性。

图4 网络参数的AUC值
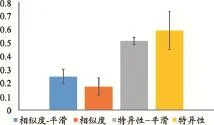
图5 个体网络脑区节点中介性指标的相似度与特异性
3 讨论
随着sMRI成像技术的快速发展,复杂网络及图论分析的方法被用来分析大脑网络的内部关联性。由于sMRI的易获取等优点,利用sMRI构建大脑结构网络得到了专家学者们的高度重视,各种新的方法也不断涌现。本研究将基于KL散度的个体脑网络成功延伸到了小鼠脑MRM个体结构网络的研究中,构建的个体灰质网络满足小世界属性,这应该是第一个基于结构特征的小鼠脑网络。与随机网络相比,构建的灰质网络具有较高的聚类系数、局部效率,以及与随机网络相近的最短路径长度与全局效率。当前,对于灰质结构网络的具体生理意义还不是十分明确,笔者认为它有可能与大脑发育过程中各个脑区的协同工作有关。即使一个简单的功能,大脑都需要调动多个脑区的协同工作来完成。当这些脑区协同工作时,非常可能会促进这些脑区内部的细胞协同发育,而在脑图像中这些脑区可能会出现较相近的神经细胞分布。
空间平滑操作是神经影像处理中的一种常用操作,它可以用来提高图像的信噪比和减小配准误差带来的脑区划分差异。由于小鼠大脑体积较小,每个体素的体积也非常小,图像信噪比较差。同时,由于小鼠大脑的个体差异性相对人脑也较少,所以对配准算法提出了较高要求[36]。因此空间平滑操作对于小鼠图像是存在一定必要性的。结果显示,平滑图像生成的脑网络仍然具有小世界特性,同时多种网络参数的AUC结果显示,个体对象的网络参数的个体特异性减小。脑区重要性的研究也显示平滑处理可以提高不同个体脑区节点重要性的相似度和降低其特异性。由于平滑操作会在一定程度上改变脑网络的拓扑结构,因此在未来的研究中还需要进一步研究不同平滑程度对网络的影响。一个好的平滑参数应该是可以在降低噪声的同时,具有较高的网络检测敏感性,可以检测出各种其它因素(如年龄,疾病等)对脑网络的影响。Hub的研究结果显示,对于不同个体,网络节点的重要性具有较大的特异性和较小的相似度,这可能是由于多种原因造成的。首先,小鼠MRM图像的体素大小为人脑的千分之一,图像的信噪比较低。由于网络中连接边的计算是基于各脑区的灰度分布实现的,噪音对于结果的影响可能较大。后期工作一方面需要通过模拟仿真研究信噪比对网络特异性的影响,另一方面可以加长对活体小鼠图像采集时间,或采用离体小鼠图像,提高图像的信噪比。其次,采用的数据库中的小鼠图像前期已经做过灰度归一化,这部分可能存在舍入误差,对网络分析结果造成一定影响。
当然,本研究还存在一些不足之处。首先,基于图像灰度建立的结构网络,虽然在一定程度上可以反映脑区中神经细胞的分布信息,但并不能反映小鼠大脑中各个脑区的形态变化。后期可能需要通过变形域对图像进行调制,使得网络可以反映形态学的变化。另外,研究对象的脑区划分并没有区分左右脑,在下一步的研究中笔者希望将脑区划分为左右脑,进一步研究左右脑的协同化工作以及脑区间存在的长程连接。
[1]Sporns O,Tononi G,Kötter R.The human connectome: A structural description of the human brain[J].Plos Computational Biology, 2005,1(4):e42.
[2]Sporns O.The human connectome: origins and challenges[J].Neuroimage,2013,80(1):53-61.
[3]Sporns O.Networks of the Brain[M].USA:MIT Press,2011:18578-18578.
[4]林岚,付振荣,张柏雯,等.DTI脑连接组在大脑疾病方面的研究进展[J].中国医疗设备,2015,30(6):1-6.
[5]Sheline YI,Price JL,Yan Z,et al.Resting-state functional MRI in depression unmasks increased connectivity between networks via the dorsal nexus[J].P Natl Acad Sci USA,2010,107(24):11020-11025.
[6]林岚,张柏雯,徐小亭,等.大脑老化对大规模皮层网络拓扑结构的影响[J].中国医疗设备,2015,30(6):12-17.
[7]Scheeringa R,Petersson KM,Oostenveld R,et al.Trial-by-trial coupling between EEG and BOLD identif es networks related to alpha and theta EEG power increases during working memory maintenance[J].Neuroimage,2009,44(3):1224-1238.
[8]De PF,Della PS,Snyder AZ,et al.Temporal dynamics of spontaneous MEG activity in brain networks[J].P Natl Acad Sci USA,2010,107 (13):6040-6045.
[9]Petersen SE,Sporns O.Brain Networks and Cognitive Architectures[J].Neuron,2015,88(1):207-219.
[10]Lin L,Jin C,Fu Z,et al.Predicting healthy older adult’s brain age based on structural connectivity networks using artificial neural networks[J].Comput Meth Prog Bio,2016,125:8-17.
[11]Franke K,Ziegler G,Klöppel S,et al.Estimating the age of healthy subjects from T1-weighted MRI scans using kernel methods: Exploring the influence of various parameters[J].Neuroimage,2010,50(3):883-892.
[12]Seeley WW,Crawford RK,Zhou J,et al.Neurodegenerative diseases target large-scale human brain networks[J].Neuron,2009,62(1):42-52.
[13]Supekar K,Menon V,Rubin D,et al.Network Analysis of Intrinsic Functional Brain Connectivity in Alzheimer’s Disease[J].Plos Comput Bio,2008,4(6):1-11.
[14]Bassett DS,Bullmore ET.Human Brain Networks in Health and Disease[J].Curr Opin Neurol,2009,22(4):340-347.
[15]Alexander GE,Bergfield KL,Chen K,et al.Gray matter network associated with risk for Alzheimer’s disease in young to middle-aged adults[J].Neurobiol Aging,2012,33(12):2723.
[16]He Y,Chen ZJ,Evans AC.Small-World Anatomical Networks in the Human Brain Revealed by Cortical Thickness from MRI[J].Cerebral Cortex,2007,17(10):2407-2419.
[17]Tijms BM,Seriès P,Willshaw DJ,et al.Similarity-Based Extraction of Individual Networks from Gray Matter MRI Scans[J].Cerebral Cortex, 2012,22(7):1530-1541.
[18]Kong XZ,Wang X,Huang L,et al.Measuring individual morphological relationship of cortical regions[J].J Neurosci Meth,2014,237:103-107.
[19]Benveniste H,Blackband S.MR microscopy and high resolution small animal MRI: applications in neuroscience research[J].Prog Neurobiol,2002,67(5):393-420.
[20]Lin L,Fu Z,Xu X,et al.Mouse brain magnetic resonance microscopy: Applications in Alzheimer disease[J].Microsc Res Techniq, 2015,78(5):416-424.
[21]Wang H,Jin X,Zhang Y,et al.Single-subject morphological brain networks: connectivity mapping,topological characterization and test–retest reliability[J].Brain Behav,2016,6(4):448.
[22]Bassett DS,Bullmore E,Verchinski BA,et al.Hierarchical organization of human cortical networks in health and schizophrenia[J].J Neurosci,2008,28(37): 9239-9248.
[23]Bai J,Trinh TLH,Chuang KH,et al.Atlas-based automatic mouse brain image segmentation revisited: model complexity vs.image registration[J].Magn Reson Imag,2012,30(6):789-798.
[24]Lin L,Wu S,Bin G,et al.Intensity inhomogeneity correction using N3 on mouse brain magnetic resonance microscopy[J].J Neuroim aging,2013,23(4):502-507.
[25]林岚,郝冬梅,白燕萍,等.7T MRI 系统在脑图像中的应用研究进展[J].生物医学工程学杂志,2013,30(5):1127-1130.
[26]Sled JG,Zijdenbos AP,Evans AC.A nonparametric method for automatic correction of intensity nonuniformity in MRI data[J].IEEE Trans Med Imag,1998,17(1):87-97.
[27]Paxinos G,Franklin KBJ.The mouse brain in stereotaxic coordinates[M].Oxford:Gulf Professional Publishing,2004.
[28]MacKenzie-Graham A,Lee EF,Dinov ID,et al.A multimodal, multidimensional atlas of the C57BL/6J mouse brain[J].J Anat, 2004,204(2):93-102.
[29]Wang J,Wang X,Xia M,et al.GRETNA: a graph theoretical network analysis toolbox for imaging connectomics[J].Front Human Neurosci,2015,9:386.
[30]Wang JH,Zuo XN,Gohel S,et al.Graph Theoretical Analysis of Functional Brain Networks: Test-Retest Evaluation on Shortand Long-Term Resting-State Functional MRI Data[J].Plos One,2011,6(7):e21976-e21976.
[31]Maslov S,Sneppen K.Specificity and stability in topology of protein networks[J].Science,2002,296(5569):910-913.
[32]Bassett DS,Bullmore E.Small-World Brain Networks[J].Neurosci
entist,2006,12(6):512-523.
[33]Achard S,Salvador R,Whitcher B,et al.A resilient,low-frequency, small-world human brain functional network with highly connected association cortical hubs[J].J Neurosci,2006,(26):63-72.
[34]Batalle D,Eixarch E,Figueras F,et al.Altered small-world topology of structural brain networks in infants with intrauterine growth restriction and its association with later neurodevelopmental outcome[J].Neuroimage,2012,60(2):1352-1366.
[35]Jin C,Lin L,Kuo LW,et al.The relationships between the identif ed critical nodes within DTI-based brain structural network using hub measurements and vulnerability measurement[C].37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC).IEEE,2015:422-425.
[36]Fu Z,Lin L,Jin C.Symmetric image normalization for mouse brain magnetic resonance microscopy[C].International Conference on Advances in Mechanical Engineering and Industrial Informatics,
Study on the Construction of Individual Structure Network Based on Gray Level Distribution of Mouse Brain MRM Image
The Structure Magnetic Resource Imaging (sMRI) network analysis, one of the most popular techniques for neuroimaging analysis, which integrates the techniques of the sMRI, imaging processing, complex networks and graph theory analysis et al, gives us a good understanding of the brain structural organization and its relationship with diseases. Nowadays, the network analysis for human brain based on sMRI has attracted researchers’ attention, while the study for mouse brain magnetic resource microscopy is relatively rare. In this paper, the individual mouse structural networks were constructed based on Kullback-Leibler divergence of regional intensity distribution and a further analysis of network topology properties was made. This method can be used to study the age and disease related brain network changes in mouse brain.
mouse brain; individual brain network; Kullback-Leibler divergence
FU Zhen-rong, LIN Lan, ZHANG Bai-wen, WU Shui-cai
College of Life Science and Bioengineering, Beijing University of Technology, Beijing 100124, China
R445.2
A
10.3969/j.issn.1674-1633.2016.12.004
1674-1633(2016)12-0017-06
2016-11-15
北京市自然科学基金资助项目(7143171);国家科技支撑计划课题(2015BAI02B03)。
林岚,副教授。
通讯作者邮箱:lanlin@bjut.edu.cn
