基于滑移网格的潜艇旋臂试验数值模拟*

邓　峰,戴余良,陈志法,张百勇

(1.海军工程大学,湖北武汉　430033;2.解放军61139部队,福建漳州　363000)



基于滑移网格的潜艇旋臂试验数值模拟*

邓峰1,戴余良1,陈志法2,张百勇1

(1.海军工程大学,湖北武汉430033;2.解放军61139部队,福建漳州363000)

摘要:潜艇水动力系数对潜艇操纵性研究具有重要意义。为了获取较高精度的潜艇旋转导数,以分区结构化网格为基础,采用基于固定坐标系的滑移网格方法,对SUBOFF潜艇进行旋臂试验数值仿真。并对比两种不同的湍流模型下仿真结果,误差均在8%以内,满足工程要求,验证了方法的可行性。

关键词:潜艇;滑移网格;旋臂试验;数值模拟;湍流

修回日期： 2015-12-04

戴余良(1966-),男,博士,副教授。

陈志法(1990-),男,硕士。

张百勇(1990-),男,硕士研究生。

潜艇是现代海军重要作战装备,其水动力系数的获取对潜艇操纵性研究有重要意义。采用计算流体力学方法(CFD)对潜艇操纵性预报已经成为一个重要的研究方向。

文献[1]等采用定常旋转运动坐标系,比较了不同湍流模型及网格分布对水下航行体做单平面回转运动所受力及力矩预报结果的影响,表明数值预报方法是有效可行的。文献[2]等讨论了潜艇的位置、姿态和舵角的关系,建立了潜艇回转运动参数与舵角信息的数学模型和适用于仿真的仿真模型。文献[3]等用CFD方法构建了“带自由液面的水面舰船数值回转水池”,对船模进行了回转运动的数值仿真,准确地再现了回转过程中的各种宏观流动现象。文献[4]等以结构化网格为背景,采用添加动量源项的方法对旋转导数进行预报,将潜艇旋臂试验转化为定常导数进行求解,提高了旋转导数的预报精度。文献[5]等通过UDF及动网格技术,对匀速运动和匀加速运动的SUBOFF模型进行了分析,并通过换算和数值拟合处理得到了潜艇所受的惯性力和惯性类水动力系数。文献[6]等应用FLUENT软件对潜艇的旋臂试验进行数值模拟,得到系列的水动力导数,并对比文献结果说明方法是可行的。文献[7]等根据旋臂试验特点,采用分区混合网格结合MRF方法解决船体圆运动及螺旋桨定轴旋转运动的叠合难题。国内对潜艇旋转导数求取虽取得一定成果,但尚处于发展阶段,从方法上还不能兼顾精度与效率问题。

滑移网格方法设置简单,对螺旋桨[8]、搅拌器的模拟取得较好结果,但是用该方法求取潜艇旋转导数在国内还较少,本文将尝试用该方法计算潜艇旋转导数时的计算效率和计算精度做一些有益探究。本文以SUBOFF潜艇为研究对象,利用ICEM CFD划分结构化网格,分别选取RNGk-ε和标准k-ω2种不同湍流模型,采用滑移网格方法对潜艇旋臂试验进行数值模拟,求取不同湍流模型下的旋转导数并对比试验数据[9],发现仿真误差在8%以内,满足工程需求,表明本研究对潜艇旋转导数求取有一定参考价值。

1控制方程与基本理论

1.1控制方程

潜艇流场流质为不可压缩粘流,其基本控制方程由连续性方程和RANS方程组成,张量形式[10]为:

(1)

(2)

1.2湍流模型

采用湍流模型RNGk-ε和标准k-ω使控制方程封闭,借以考察两种模型对潜艇旋臂试验数值仿真精度,为了节省篇幅,下面仅给出两种模型的数学表达式,详细的推导过程和各参数的选取可参考文献[11]。

1)RNGk-ε模型

湍动能k方程:

(3)

湍耗散率ε方程:

(4)

2)标准k-ω模型

湍动能k方程:

(5)

特殊耗散率ω方程:

(6)

1.3数值计算方法

以上两种模型均采用有限体积法(FVM)对控制方程和湍流模型进行离散,压力速度耦合迭代采用SIMPLEC算法,动量方程、湍流动能方程、耗散率方程采用二阶迎风格式,考虑计算收敛性,采用欠松弛技术,速度欠松弛因子、湍动能松弛因子、特殊耗散率松弛因子均取0.3,其他取默认值。残差收敛均取为0.0001。

1.4滑移网格

当采用定坐标系时,网格随潜艇做回转运动(本文指的是內域网格整体运动,外域不动,外域物理量由內域插值传递,旋转中心为(0,0,0),旋转轴为(0,0,1))。此时,回转运动是非定常的,通过这种方式进行迭代时,网格不会发生变形,避免网格畸变而影响计算精度。

2模型与网格划分

2.1模拟对象

本文以SUBOFF AFF-1(裸艇体)和AFF-8(全附体)潜艇模型为数值模拟对象。模型主尺度L=4.356m,其中前体长1.016m,平行中体长2.229m,后体长1.111m,最大直径为0.508m,全附体模型如图1所示,裸艇体为全附体主艇体部分,不再赘述。

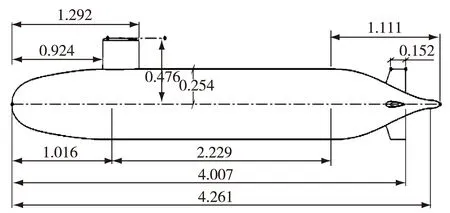
图1　SUBOFF AFF-8潜艇模型

2.2边界条件

为满足滑移网格特性,计算域分为內域和外域,外域为一包裹內域的圆环,最外半径为26m,最内半径为10m,潜艇体力矩中心与文献[9]一致,以过潜艇力矩中心线为母线,旋转拉伸正方形生成內域。计算域内流体为不可压缩水介质,不考虑重力,计算域模型示意如图2所示，边界条件如图3所示。

图2　计算域模型

图3　边界条件

外域壁面:设置为静止壁面边界,其他取默认值;

內域壁面:设置为interface,以便内外域网格进行相对移动;

潜艇壁面:设置为随区域运动的壁面边界(Moving Wall),旋转中心为(0,0,0),旋转轴为(0,0,1),相对于临近网格单元静止。

2.3网格划分

结构网格能够节省大量的内存空间,拥有更高的计算效率,本文采用分区网格技术划分结构网格。运用商业网格划分软件ICEM CFD对潜艇外流场进行网格划分。其中,裸艇体网格总数量为80万,全附体150万。划分策略相似,仅以裸艇体网格划分为例:首先划分外域网格,由2D Planar旋转拉伸为10个块,每个块旋转角度为36°,再生成内O-Block,删除內域部分,将剩余块的內表面与內域壁面进行映射,块外表面与外域表面进行映射,并对网格进行加密,生成外域网格保存后关闭。然后划分內域网格,同样由2D Planar旋转拉伸后,全局缩放因子选1,在全局单元尺寸为1的基础上对局部进行加密。潜艇周围划分外O-Block,以便边界层处理,边界层内单元增长率为1∶1.1;边界层到流场边界单元增长率为1∶1.2,在其他地方采用H型网格,确保网格质量在0.6以上。边界层内节点数设为31,第一层网格高度为0.1mm,使壁面Y+值在30左右,选用标准壁面函数;对应与弧度部分特殊加密。最后,生成內域网格后打开外域网格进行合并,生成最终整体流域网格,艇体网格划分结果如图4所示。

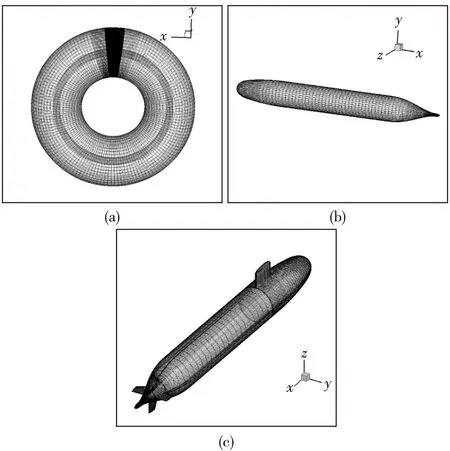
图4　流场网格(a)和潜艇表面网格(b)、(c)示意图

3计算结果与分析

水动力系数为无因次化结果,力和力矩旋转导数无因次化表达式为:

(7)

其中,ρ为液态水密度,取ρ=998;V为潜艇旋转线速度;L为潜艇垂线间长,按文献[9]取L=4.261m;Yr为Y向受力;Nr为Z轴力矩,力矩中心与其它文献一致,本文中为(0,18,0)。计算前先使用旋转坐标系方法定常计算1000步,以获得稳定流场。此时为非定常计算的初始时刻,对其进行滑移网格设置:外域静止,內域设置为滑移网格进行非定常计算,计算步长为0.005s,每个时间步迭代20次,共计算8s,1600步。网格旋转角速度r分别为:0.1,0.2,0.3,0.4,0.5rad/s。

图5　RNGk-ε模型下横向力旋转导数(a)和转艏力矩旋转导数(b)拟合曲线

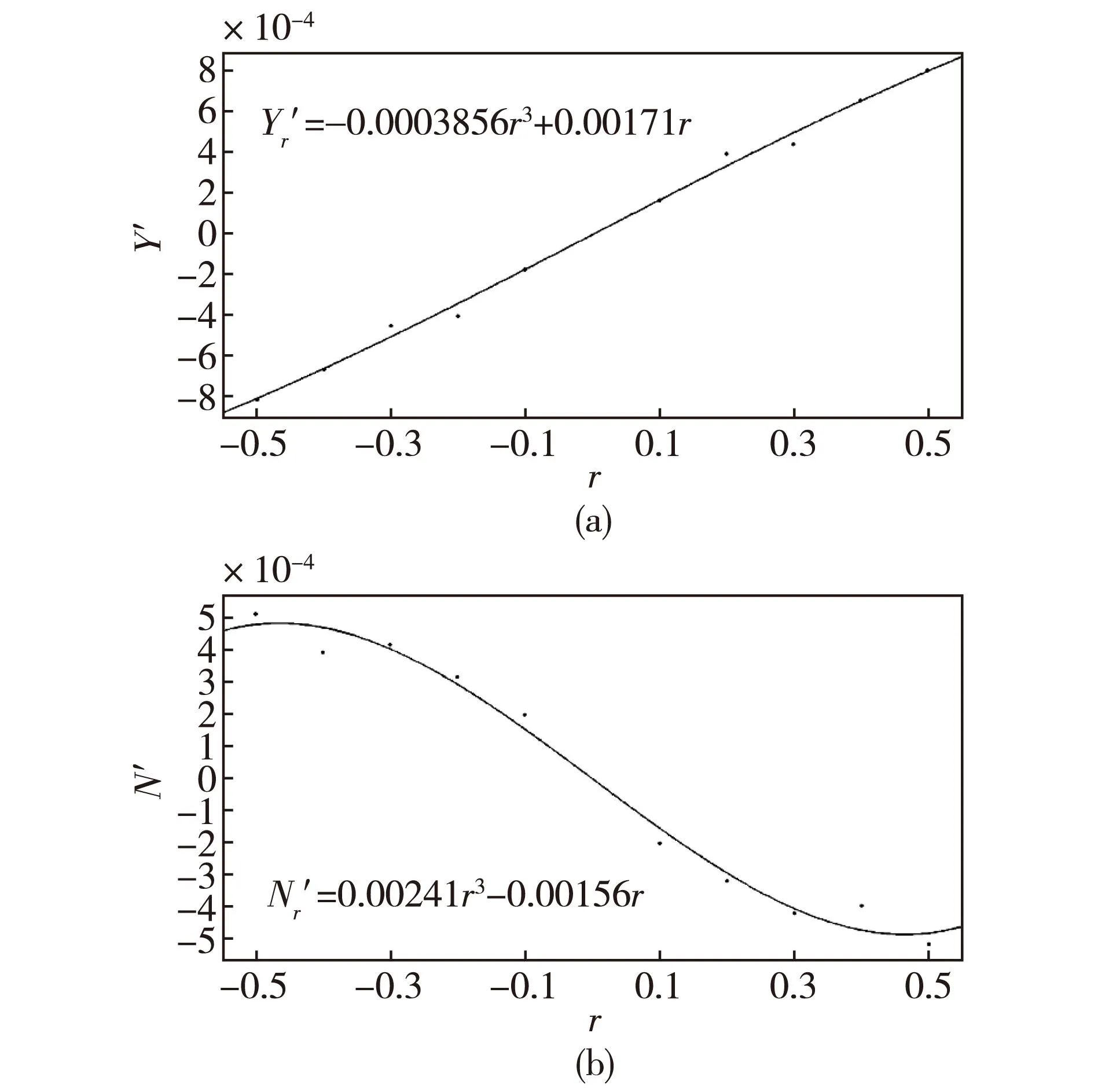
图6　标准k-ω模型下横向力旋转导数(a)和转艏力矩旋转导数(b)拟合曲线

旋转导数计算结果试验结果相对误差%Y'r0.0016710.001811-7.7N'r-0.001501-0.001597-6.0

表2　标准k-ω湍流模型下拟合与试验结果对比

图7　RNGk-ε模型下横向力旋转导数(a)和转艏力矩旋转导数(b)拟合曲线

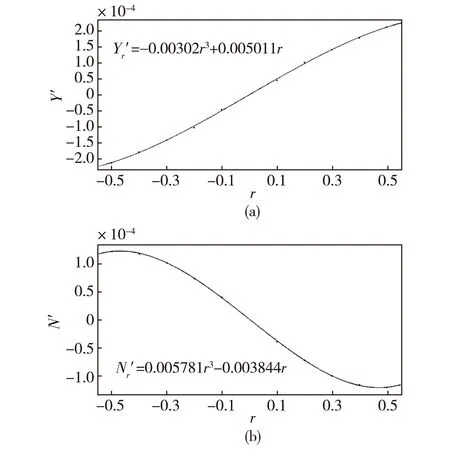
图8　标准k-ω模型下横向力旋转导数(a)和转艏力矩旋转导数(b)拟合曲线

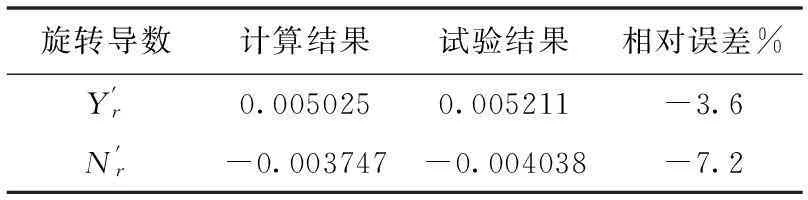
旋转导数计算结果试验结果相对误差%Y'r0.0050250.005211-3.6N'r-0.003747-0.004038-7.2

表4　标准k-ω湍流模型下拟合与试验结果对比

以裸艇体在RNGk-ε湍流模型下旋转角速度为0.5rad/s的计算结果为例,图9为流场Z=0切面0s,2s,4s,6s,8s的速度云图。

图9　Z=0切面不同时刻速度云图(a)-(e)

2)该方法计算时长较长(普通计算器i5四核,裸艇体单个计算耗时为8h,全附体单个计算耗时为23h),计算效率一般,更适用于高性能的计算器进行仿真。

4结束语

本文通过SUBOFF潜艇在两种湍流模型下,运用滑移网格方法对其旋转导数进行仿真模拟,并与试验数据相比,精度能够达到工程应用要求,更适合在高性能计算器下仿真,本文的研究内容对潜艇旋转导数求取有一定参考价值。

参考文献:

[1]卢锦国,梁中刚,周轶美,等. 湍流模型及网格分布对水下航行体回转水动力数值计算影响研究[C].第七届中国CAE工程分析技术年会论文集,2011:179-186.

[2]刘勤贤,朱根兴,吕炜.潜艇回转运动模型建立与仿真[J].计算机测量与控制,2003,11(1): 62-77.

[3]蒋奉兼,陈敏,程捷等.带自由液面的水面舰船回转运动水动力数值计算方法研究[C].第十一届全国水动力学学术会议暨第二十四届全国水动力研讨会暨周培源教授诞辰110周年纪念大会文集,2012:975-981.

[4]刘帅,葛彤,赵敏.基于源项法的潜艇旋臂试验模拟[J]. 大连海事大学学报,2011,37(2): 1-4.

[5]肖昌润,刘瑞杰,刘洋等.水下航行体惯性类水动力系数的计算方法[J]. 海军工程大学学报,2014,26(5): 44-47.

[6]詹成胜,刘祖源,程细得.潜艇水动力系数数值计算[J].船海工程,2008,37(3): 1-4.

[7]王骁,蔡烽,石爱国等.双桨双舵舰船旋臂试验粘性流场数值模拟方法研究[J].船舶力学,2014,18(7):787-793.

[8]姚震球,高慧,杨春蕾.基于滑移网格的带螺旋桨艇体尾流场数值分析方法[J].江苏科技大学学报(自然科学版),2008,22(2):15-20.

[9]Roddy R.F. Investigation of the Stability and Control Characteristics of Several Configurations of the DARPA SUBOFF Model(DTRC Model 5470)from Captive-Model Experiments[R].David Taylor Research Center,1990.

[10]张楠,沈泓萃,姚慧之.潜艇阻力与流场的数值模拟与验证及艇型的数值优化研究[J].船舶力学,2005,9(1):1-13.

[11]王福军.计算流体动力学分析——CFD软件原理与应用[M].北京:清华大学出版社,2006.

Sliding Mesh Based on Numerical Simulation of Rotating Arms Tests for Submarines

DENG Feng1, DAI Yu-liang1, CHEN Zhi-fa2, ZHANG Bai-yong1

(1.Naval University of Engineering, Wuhan 430033;2. the Unit 61139 of PLA, Zhangzhou 363000, China)

Abstract:The hydrodynamic coefficients are significant for the hydrodynamic performance of submarine. To obtain the rotary derivative of submarine with high precision, the structured mesh and sliding mesh with fixed coordinates are adopted. Simulations based on SUBOFF submarine are performed in two different turbulent models, and the simulation results are compared with the experimental data. The numerical simulation error shows to be under 8%, which is satisfied with the engineering requirement and verify the feasibility of this method.

Key words:submarine; sliding mesh; rotating arm tests; numerical simulation; turbulence

作者简介：邓峰(1990-),男,湖北黄石人,硕士研究生,研究方向为潜艇操纵与运动仿真研究。

*基金项目：国家自然科学基金(51179196)

收稿日期：2015-09-30

中图分类号:U674.76；E925.66

文献标志码:A

DOI:10.3969/j.issn.1673-3819.2016.01.026

文章编号：1673-3819(2016)01-0122-05