高海情对反导舰炮命中概率的影响

王立红，宋　军

(解放军92941部队,辽宁葫芦岛　125001)



高海情对反导舰炮命中概率的影响

王立红，宋军

(解放军92941部队,辽宁葫芦岛125001)

摘要:根据某型反导舰炮配装的舰船摇摆特性及海浪运动数学模型,首先模拟得到高海情舰船摇摆趋势图;然后分析了高海情对反导舰炮射击诸元的影响;其次,采用变换抽样法在高海情射击诸元变化范围内随机产生方位角和高低角增量,通过解6自由度弹道方程计算方位角和高低角增量概率误差,再根据概率误差解算高海情条件下系统的命中概率;最后,对大量的仿真计算结果进行统计分析,得出了具有实用价值的结论,为靶场试验及系统精度设计提供参考。

关键词:高海情；反导舰炮；概率误差；命中概率

修回日期： 2015-10-21

宋军(1978-),男,硕士,工程师。

随着以联合作战为特征的武器装备作战使用模式的转变,边界条件下武器的作战效能在一定程度上决定了战争的胜负。反导舰炮武器的作战效能与火控解算精度及命中概率息息相关。高海情摇摆条件作为海上允许使用武器的边界条件,直接影响火控解算精度及命中概率。目前,靶场对反导舰炮武器边界条件试验鉴定理论及方法还处于探索阶段。所以,有效判定高海情对弹道散布及命中概率的影响是武器系统精度设计的要求,也是靶场舰炮武器试验鉴定的急需。

1高海情条件下舰船摇摆特性仿真

1.1舰船摇摆特性数学模型及参数解析

不规则的海浪,可以看成是由无数频率、波长不同的波形呈正弦的规则波叠加而成[1]。船模试验结论表明,采用三次谐波叠加的方法可以模拟表示舰船海上摇摆特性。

设海浪各次谐波的幅值分别为A1、A2、A3;角频率分别为ω1、ω2、ω3;初始相位φ1、φ2、φ3,则舰船摇摆特性数学模型可以表示为

A(t)=A1sin(ω1t+φ1)+A2sin(ω2t+φ2)+

A3sin(ω3t+φ3)

(1)

下面分别说明本文在仿真计算时对模型中摇摆幅值、角频率及相位三个参数的解算方法。

1) 舰船摇摆幅值算法

设某型舰摇摆特性及某型反导舰炮工作条件为:横摇A1+A2+A3的最大值15°,纵摇A1+A2+A3的最大值7°。根据海上允许使用武器条件,并与高海情、中海情和低海情三种海况相对应,将摇摆幅值分为高、中、低三档,如表1所示。

表1　摇摆幅值

2) 舰船摇摆角频率算法

根据舰船及反导舰炮系统工作条件要求,取横摇平均周期为9s,纵摇平均周期为6s。因为2π/ω=T,所以在高、中、低三种海况下,横摇角频率ω=(ω1+ω2+ω3)/3=2π/9,纵摇角频率ω=(ω1+ω2+ω3)/3=2π/6,即可得到摇摆角频率数据。

3) 船船摇摆相位算法

由公式φi=2π*Rand(1)产生[0,2π]随机数,作为各次谐波的初相位,三次谐波叠加即可随机产生一定海况下某一时刻相位数据。

1.2高海情条件下舰船摇摆特性仿真

按照以上舰船摇摆模型及幅值、角频率和相位算法,采用Matlab语言[2]编程并进行仿真计算,随机模拟某一瞬间高海情舰船摇摆特性。

若纵横摇平均周期取10s为一个历程,0.16s为间隔,横摇角频率取ω1=0.628Hz,ω2=0.681 Hz,ω3=0.733Hz;横摇幅值A1=9.5°,A2=11.5°,A3=15.0°;纵摇角频率ω1=0.942Hz,ω2=0.995Hz,ω3=1.047Hz;纵横幅值A1=4.5°,A2=6.0°,A3=7.0°;随机模拟纵、横摇相位并进行仿真计算;得到高海情条件下该舰船摇摆特性曲线,如图1所示。

图1　高海情舰船摇摆特性示意图

由图1可见,高海情条件下该舰船摇摆特性基本为正弦波型,横摇幅值范围为±12°,纵摇幅值范围为±9°。下面依据此摇摆特性,具体分析高海情对射击诸元的影响。

2高海情条件下舰船摇摆对反导舰炮射击诸元的影响分析

2.1坐标系及公式

(2)

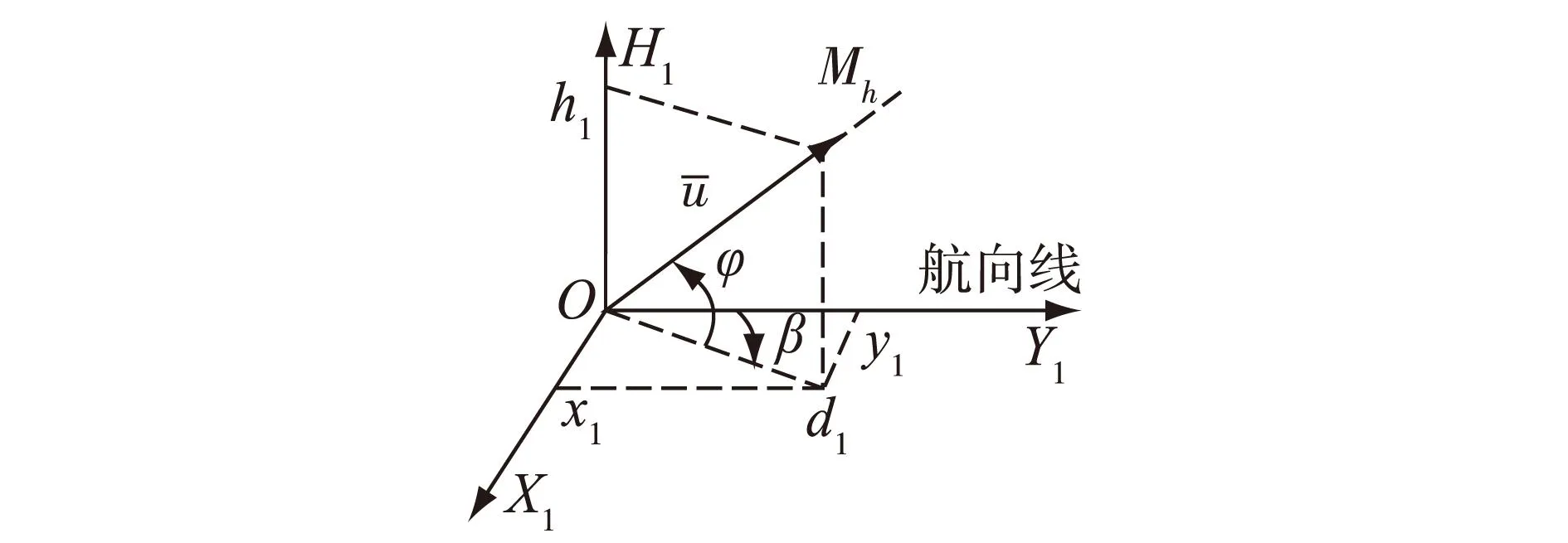
图2　稳定坐标系

图3　不稳定坐标系

(3)

(4)

2.2高海情对反导舰炮射击诸元的影响

根据高海情舰船摇摆特性仿真示意图1可以得到t时刻的横摇角θ和纵摇角ψ,设高低瞄准角φ为20°,方向瞄准角β为45°,则依据公式(3)和公式(4)就可以计算出t时刻的βn和φn,进而求出t时刻的方向瞄准角和高低瞄准角变化量Δβ和Δφ。

利用舰船摇摆特性图1的数据进行仿真计算,求解在10s的时间历程内方向瞄准角和高低瞄准角变化量,即可得出高海情条件下舰船摇摆对方位和高低瞄准角的影响,结果如图4所示。

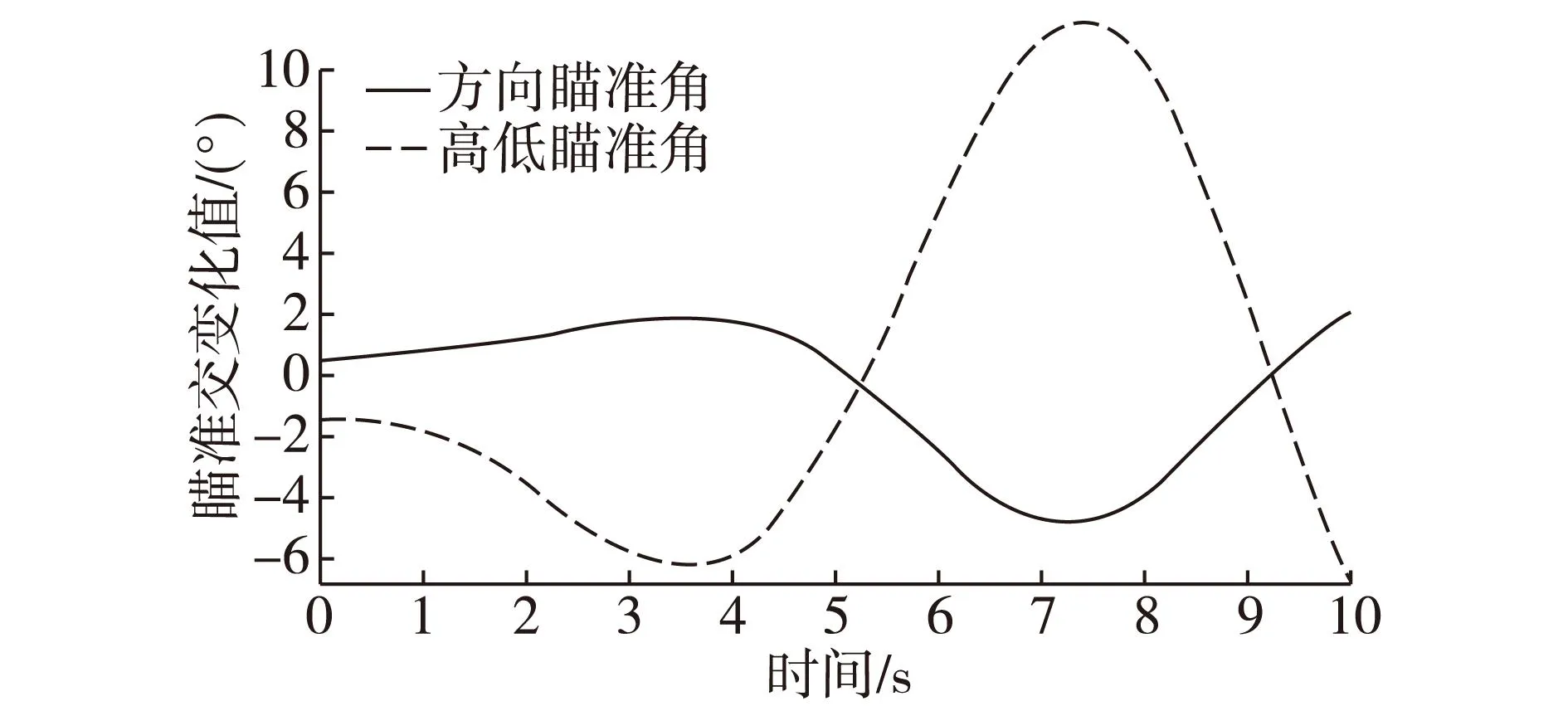
图4　高海情对诸元瞄准角的影响示意图

由图可见,在高海情的条件下,舰艇摇摆对反导舰炮射击诸元高低瞄准角影响的范围是-6°-12°,对射击诸元方向瞄准角的影响范围是-5°-2°,这种影响是形成舰炮弹道散布的重要因素,也直接影响了反导舰炮系统的命中概率。

3高海情条件下舰船摇摆对反导舰炮命中概率影响分析

在高海情条件下, 舰艇摇摆使弹丸发射瞬间的射角及射向发生变化直接影响了反导舰炮的命中概率。下面通过变换抽样法模拟产生随机射角和方向瞄准角变化量,利用此射角、射向求解6自由度弹道方程[4],计算海面或某一高度某一目标点上落点坐标及距离方向或高度方向的概率误差,由此概率误差计算对靶弹的直接命中概率[5-9]。

3.1瞄准角变化量的概率误差算法

1) 用乘同余法随机数产生器产生(0,1)均匀分布的随机数

(5)

取M=231-1,c=75=16807,x0=1,i=1,2，…，50，即

(6)

则ξi即为50个(0,1)上均匀分布的随机数。

2) 用变换抽样法产生正态分布的随机变数

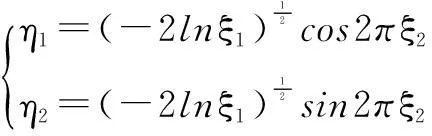
3) 求取高低和方位瞄准角增量的概率误差

设高海情条件下高低和方位瞄准角的变化是成正态分布的, 用变换抽样法产生2组正态分布的随机数各100个,按照本文求取的高海情对射角增量和方向角增量的影响范围(高低瞄准角-6°～12°,方位瞄准角-5°～2°),在每组随机数中各选择54个随机数如表2所示,分别作为高低角增量Δβi和方位角增量Δφi的随机变化量。

应用公式(7)和(8)计算高低和方位瞄准角增量的概率误差Eφn和Eβn：

(7)

(8)

3.2单炮弹道散布及命中概率算法

1) 单炮弹道散布概率误差算法

高海情条件下,已知瞄准角增量的概率误差,单炮距离、方向的散布概率误差可按公式(9)和公式(10)求取，即

(9)

(10)

其中，Ed0、Ez0为舰炮在陆上靶场的散布概率误差,可以在舰炮基本射表中查得,fdθ0为射角改变一个密位引起距离改变量,可从修正表中查得,Eφn、Eβn为舰炮由火控实施瞄准时高低和方位瞄准角增量的概率误差。

2) 命中概率算法

已知单炮弹道散布概率误差,按公式(11)求取弹着散布在某一平面区域s内的概率ps,即为反导舰炮命中概率，即

(11)

其中，Eds、Ezs为单炮距离、方向散布的概率误差。

3.3高海情条件下反导舰炮命中概率仿真计算及结果分析

设弹丸直径d=0.03m, 初速v0=1000.0m/s, 每个点射为60连发,打击目标为长10m,宽3m,高3m导弹靶,有效拦截距离(2000m,500m),全航路单炮射击至少命中1发的概率均值为0.5。以导弹靶中心点O(5m,1.5m,1.5m)靶心为坐标原点建立坐标系,选定24组火控系统高低角精度Eθ和方位角精度Eβ组合,对每一组精度按3.1算法计算射角和方向瞄准角随机变化量,按3.2算法计算命中概率。下面分别针对海面目标、超低空目标、大射角高空目标、小射角低空目标等情况进行仿真计算,具体分析高海情条件下该型反导舰炮系统对导弹靶的命中概率。

1) 水平距离x=2000m,目标位置高度h=0.0m,基准射角θ=0.522°,射角增量的概率误差为Eθ=1.3mrad,方向瞄准角增量的概率误差为Eβ=1.2mrad,进行仿真计算。

结果表明:高海情条件下,该型舰炮武器对海面目标的命中概率为P=0.10,与均值0.5相差较大,所以该型反导舰炮在高海情情条件下攻击海面目标的命中概率会大大降低。

2) 取高度分别为(0m、10m、20m、50m、100m、150 m),水平距离分别为(500m、800m、1000m、1500m、2000m、2500m、3000m),Eθ=1.7mrad,Eβ=2.1mrad,进行仿真计算。

结果表明:高海情条件下,对超低空目标射击时,该型舰炮系统的命中概率随着水平距离的增加而减小,在水平距离大约1000m左右,命中概率可达0.35,而在大于1000m的距离上P均小于0.35,同时在目标高度为70m左右时命中概率相对较高。与0.5的概率指标相比,命中概率大约下降30%。

3) 取12组Eθ、Eβ组合,高度分别为(0m、10m、20m、50m、60m、70m),水平距离分别为(800m、1000m、1200m),作为该系统打击小射角低空目标的代表,进行仿真计算。

结果表明:高海情条件下,系统以小射角对低空目标射击时,命中概率P随着射角精度概率误差Eθ和方向瞄准角概率误差Eβ的增大而减小,在Eθ=1.28mrad,Eβ=1.36mrad附近命中概率P开始到达并穿过P=0.35平面,同时命中概率P在水平距离1000 m、目标高度70m的条件下,P相对较大。

4) 取高度分别为(0m、500m、1000m、1500m、2000m,2500m、3000m),水平距离分别为(500、1000m、1500m、2000m、2500m、3000m、3500m),Eθ=1.5mrad,Eβ=1.4mrad, 进行仿真计算。

结果表明:高海情条件下,对高空目标射击时,该型舰炮系统的命中概率随着水平距离的增加而减小,在水平距离大于1000m的距离上P均小于0.35,同时目标高度越大命中概率越小。

5) 取12组Eθ、Eβ组合,高度分别为(1000m、2000m、3000m),水平距离分别为(1500m、2500m、3500m),作为该系统打击大射角高空目标代表,进行仿真计算。

结果表明:高海情条件下,系统以大射角对高空目标射击时,命中概率P均远远小于0.5。所以在高海情条件下,反导舰炮不适合攻击大射角目标。

4结束语

不同型号的舰炮其正常使用海况条件不同,其装配的舰船耐波性不同,由于舰艇摇摆带来的随机误差对命中概率的影响不同。应用本文的方法可以初步确定:高海情作为一种边界条件对反导舰炮命中概率的影响大致为20%～30%。理论分析及工程实践表明:此方法同样适用于中大口径舰炮。但由于海况相对复杂,单纯依靠数学模型及算法得出的仿真计算结果与实际值相比会存在误差,希望可以为高海情反导舰炮命中概率试验鉴定及相关工作提供一定的技术参考。

参考文献:

[1]戴遗山. 舰船在波浪中运动的频域与时域势流理论[M].北京:国防工业出版社,1999.

[2]李强,赵伟.Matlab数据处理及应用[M].北京:国防工业出版社,2001.

[3]汪德虎,谭周寿,王建明,等.舰炮射击基础理论[M].北京:海潮出版社,1998.

[4]郭锡福,赵子华.火控弹道模型理论及应用[M].北京:国防工业出版社,1997.

[5]卫爱萍,等. 现代舰艇火控系统[M]. 北京:国防工业出版社,2008.

[6]费业泰.误差理论与数据处理[M].北京:机械工业出版社,2010.

[7]闫章更.兵器试验理论研究与实践[M].北京:国防工业出版社,2011.

[8]朱元章. 火控系统的控制与仿真[M].北京:国防工业出版社,2000.

[9]闫章更, 魏振军.试验数据的统计分析[M].北京:国防工业出版社,2001.

Hit Probability of Antimissile Naval Gun under High Sea State

WANG Li-hong, SONG Jun

(the Unit 92941 of PLA, Huludao 125001,China)

Abstract:According to sea-wave mathematical model and swing characters of the ship, firstly swing character graph of the ship equipped by an antimissile gun has been simulated under condition of high sea sate. Secondly, the effect of high sea state on the firing data has been analyzed. Thirdly, this paper produces randomly the increments of azimuth and elevation in firing data range by using with conversion sample,and calculates probability deviation of the increments by solving six-degree ballistic model, then the hit probability under high sea sate condition can be derived. Finally, statistical analysis on hundreds of simulation results has been carried out, and an utility conclusion is presented,which can provide a valuable reference to the range test and accuracy design.

Key words:high sea state； antimissile naval gun； probable error； hit probability

作者简介：王立红(1972-),女,辽宁葫芦岛人,硕士,高级工程师，研究方向为舰炮火控理论及试验鉴定方法。

收稿日期：2015-09-14

中图分类号:TJ391；E917

文献标志码:A

DOI:10.3969/j.issn.1673-3819.2016.01.012

文章编号：1673-3819(2016)01-0053-04