基于乘客预测的邮轮定价

李之好　吕　文　刘佳倩



基于乘客预测的邮轮定价

李之好吕文刘佳倩

摘要：邮轮作为一种特殊服务商品，与一般商品的定价有着明显的区别，其价格的决定主要来自于潜在需求的变化。本文通过对同一航班内不同周期乘客的人数和价格进行预测，并且考虑了登舱后乘客的换舱。发现人们预定邮轮船票的时间服从双峰随机分布，峰值出现在第4周和第12周，而历史的价格可以近似用二次函数拟合，同时基于乘客的预测数对价格均匀调整能够取得收益最大值。

关键词：邮轮定价；价格预测；收益最大化；升舱意愿；转移矩阵

邮轮采用提前预订的方式进行售票，邮轮出发前0周至14周为有效预定周期，邮轮公司为了获得每次航行的预期售票收益，希望通过历史数据预测每次航行0周至14周的预定舱位人数、预订舱位的价格，已知某邮轮公司拥有一艘1200个舱位的邮轮，舱位分为三种，250个头等舱位，450个二等舱位，500个三等舱位。该邮轮每周往返一次，同一航次相邻两周之间价格浮动比不超过20%。现给出10次航行的实际预订总人数、各航次每周实际预订人数非完全累积表、每次航行预订舱位价格表、各舱位每航次每周预订平均价格表及意愿预订人数表、每次航行升舱后最终舱位人数分配表(详见附件中表sheet1- sheet5)[1]。

1、乘客人数预测

1.1研究思路

为了更明显看出各周实际预订人数变化值，通过对 sheet2 中累积预定人数进行拆分得到各周非累积预订人数，比较发现横向数据数值之间较为接近，但数据在时间序列上仍具有较大的波动性，因此我们主要对同一航班不同预定周的乘客人数进行预测，采用移动平均预测模型、经典增量法预测模型[2]以及灰色预测等三种在思路上差别较大的预测方法，以便对预测结果进行对比。

1.2理论建模

1.2.1移动平均预测

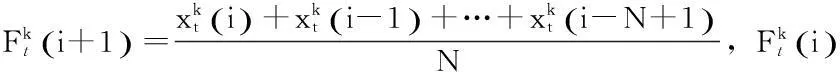
1.2.2经典增量预测

1.2.3灰色预测[3]

灰色预测GM(1,1)模型是一个拟微分方程的动态系，其建模的实质是对原始数据先进行一次累加生成，使生成的数据序列成一定规律，而后通过建立微分方程模型求得拟合曲线，用于对系统预测。

1.3结果分析

Figure1　灰色预测误差　　　　　　　Figure2　移动平均预测误差

通过上面两幅图可以看出，预测值和真实值之间存在着不小的误差，其中头等舱的误差要比二等舱和三等舱高一些原因就是头等舱作为奢侈品更易受到外部因素的影响，而二等舱和三等舱存在一定的“刚需”，因此波动会小一点，预测的结果也会更好，同时我们发现灰色预测的结果趋势非常平稳，对于趋势不太明显的变量预测效果会减弱。

2、邮轮价格预测

2.1研究思路

通过对历史价格数据的走势观察我们发现，同一航次不同订票周期的船票价格有着相对稳定的走势，因此我们可以用多项式进行趋势拟合，然后用估计出来的模型对下一周期价格进行预测。

2.2数据处理

由图5显示价格近似服从二次函数，且每个航班的预定周期为14，因此我们可设定模型[4]：

2.3结果分析

下面为不同航班三个舱位价格趋势的回归参数的结果以及回归效果“决定系数”，其决定系数为三个舱位的模型回归系数的平均数。

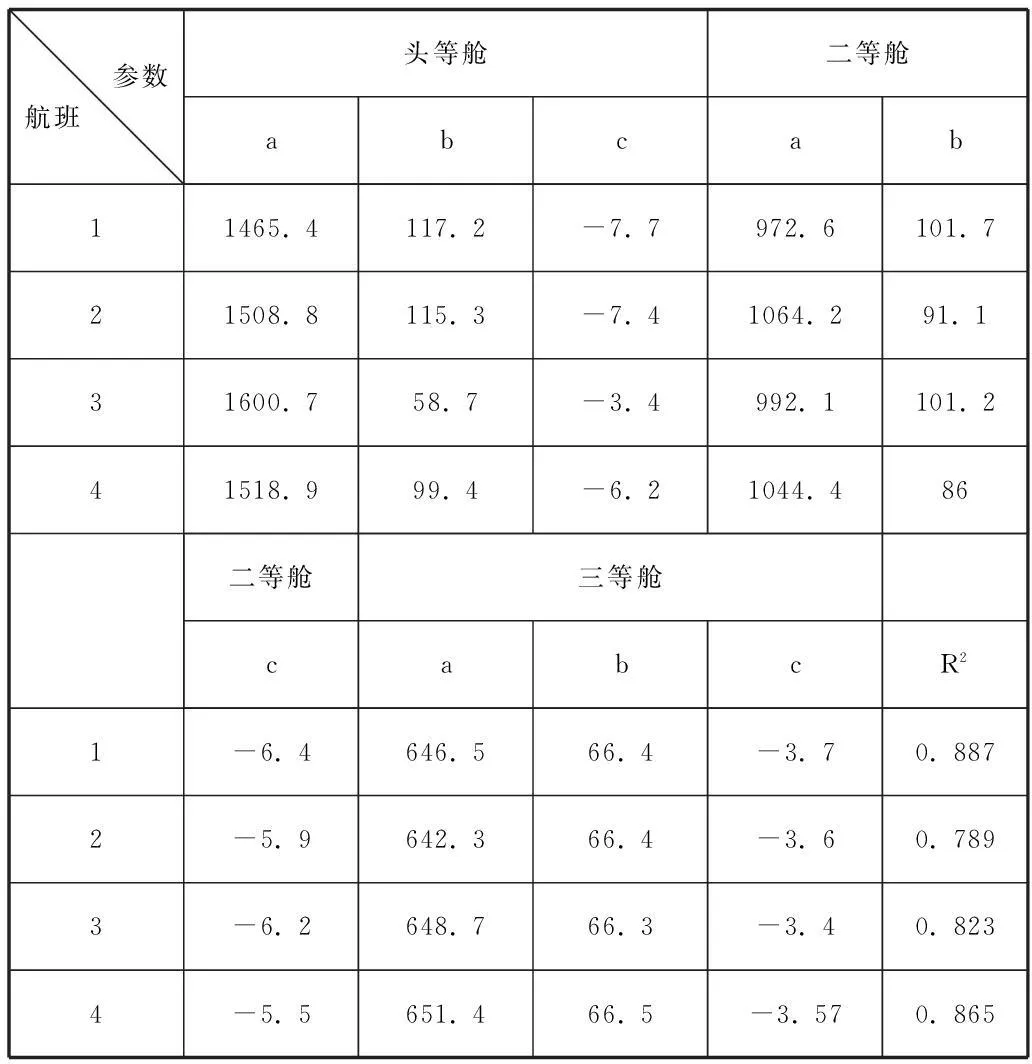
Table1　参数估计结果

3、预期收益

3.1研究思路

问题三要求建立邮轮每次航行的最大预期售票收益模型，因此问题的关键就是通过建模求解出预期需求与价格的关系——需求函数。题中假设每种舱位每周预定价格在价格区间内服从均匀分布，需求函数转为关于预定价格和意愿预定人数的函数，问题的关键则在于确定各销售周期的意愿预定人数[5]。因此我们首先基于最小二乘法，利用约束规划来确定需求函数的参数，其次，以未来总收益最大化为原则，通过一个非线性约束规划来确定最优的价格，以此建立邮轮每次航行的最大预期售票收益模型。

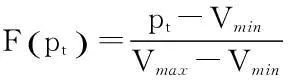
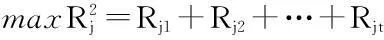
3.3结果分析

我们选取第8次航班三等不同舱位的数据带入求解计算求得结果如下表所示预，其中包含每次的价格:

Table2　第8次航班的预期收益

第8次航班总共剩余四个预定期，且为靠近开船的预定期，预测收入之和占总收益的1/10，这是因为临近开船的乘客预定数减少，价格也降低的原因，因此可以得出根据乘客预测数量制定价格的最受益会出现“凹性”，即价格和乘客同时减少同时增加，体现在收益上就是二次凹函数。

4、调舱策略

4.1研究思路

为了使利润最大化邮轮公司会在头等、二等舱未满的情况下，允许已登船的游客适当加价升舱。假设登船前的票价已经使游客舱位选择达到均衡，如果所有的舱位价格不变，就不会有人选择升舱，因此，升舱所需价格和游客登船前票价总和不得超过游客所要升舱的原始售价。

4.2升舱意愿模型

我们先假设二等舱的价格等于三等舱，结果是所有三等舱的游客都会选择二等舱，当二等舱的价格不变，则不存在人员流动，因此我们可以把三等舱的初始人数看成想要流动到二等舱的意愿人数。同理，头等舱的价格等于二等舱，结果是所有二等舱的游客和部分三等舱的游客都会选择二等舱，当头等舱的价格不变，则不存在人员流动，因此我们可以把二等舱和三等舱的初始人数看成想要流动到二等舱的意愿人数。因此我们可以建立意愿函数：

Figure3　升舱后各舱位人数变化

到二等舱的意愿函数：

升到头等舱的意愿函数：

5、结论

在前面已经说过邮轮公司的定价是基于潜在的游客人数和预定人数。在此基础上所定出的价格只是能够使每个舱位的人数最大化，但是如果实际等舱后三种舱位仍存在流动的空间

邮轮公司可以选择以降低一等舱和二等舱价格的方式来提高利润，而在卖票的初期这些都是不可预测的，因此在游客登船后再次调整价格是为了对前期最优定价误差一次修正，也是寻找真正最优价格，以取得最大收益。同时人们对于升舱的意愿函数，也是对下期船票定价的基础，减少未来定价的不合理性。同时通过对历史数据的统计分析，也能减少定价盲目性。(作者单位：安徽财经大学金融学院)

参考文献:

[1]2015年第八届电工数学建模竞赛题目B；

[2]曾五一 肖红叶.统计学导论[M].北京：科学出版社,第二版2013年1月：229-246；

[3]朱登远,常晓凤.灰色预测 GM(1,1)模型的 MATLAB 实现[J]河南城建学院学报,2013,22(3):40-46；

[4]李柏年,吴礼斌．MATLAB 数据分析法[M]．北京：机械工业出版社，2012.1；

[5]孙晓东,冯学钢.邮轮公司如何定价—基于北美市场的实证分析[J]旅游学刊,2013,28(2):111-118；

[6]孙晓东.邮轮收益管理：需求预测与收益优化[D]上海:上海交通大学,2011；

[7]张波,商豪.应用随机过程[M].北京：中国人民大学出版社,第三版2014年1月:97-102。

作者简介：李之好(1992-)，男，汉族，安徽阜阳市，本科，安徽财经大学，研究方向：金融工程。