基于灰色理论的城市对流域取水量研究

张承全

(河南省水利第一工程局，河南 郑州 450000)

基于灰色理论的城市对流域取水量研究

张承全

(河南省水利第一工程局，河南 郑州 450000)

城市对流域的取水量具有不确定性和随机性，其中涵盖灰色性；工业对流域的取水量更具灰色信息；常规的数学理论方法难以将复杂、模糊的随机过程进行可视化和定性、定量预测。灰色信息是介于白色信息和黑色信息之间的一种特殊信息，灰色理论能揭示信息的灰色性和随机性，通过甄别信息内在发展趋势的相异程度，对数据进行剖析处理，生成规律较强的数值序列，进而建立灰色系统模型，以预测数据的发展趋势。本文基于灰色理论和灰色预测，揭示原始数据的灰色性，通过级比检验和累加算子，构建灰色理论模型GM(1，1)，将该模型应用于河南省对黄河的总取水量和工业取水量。研究结果表明：灰色理论模型具有操作性强，理论与实际结合度高的优势，在数据短缺的序列中能优化模型的结果；通过模型对河南省取黄河水量的预测具有较高的精度，总取水量相对误差在3.05%～13.16%之间，工业取水量相对误差在1.61%～12.53%之间；为黄河的统一调度，优化配置水资源提供理论参考。

灰色理论；GM(1，1)；取水量；河南

城市取水量和工业取水量包含随机性和灰色信息，是一个非线性，复杂的水文过程[1-2]。在取水量预测方面，国内外研究者做了很多工作，取得了丰硕的成果。Dianep等通过介绍各国工业用水量，建立取水和再循环的评价模型，简明了技术改革中取水与再循环的比重[3]；Yano等根据水足迹理论，结合用水潜在户，建立加权模型，解决水资源用户的差异性并预测城市用水量[4]。褚桂红基于RBF神经网络的结构、原理和训练算法，建立预测模型，对城市的工业取水量进行预测并取得较高精度[5]；高珺等选取国内生产总值，跨流域调水量等因素，根据供需平衡原理，建立我国水资源供给与需求模型，对水资源供需进行实证和预测[6]；潘国强根据最小二乘法支持向量机和组合预测理论，结合万元工业GDP取水量，构建预测模型，提升短期预测模型的精度[7]。众多学者对取水量和水量进行了大量的工作，为步入下一阶段研究夯实基础。对河流的取水量受到城市产业结构与人口聚居地等的影响，是一个非线性、多因素的水文过程，存在着较大的不确定性和灰色性，故建立预测模型的难度较大，有时就算建立起了模型却因为缺少数据而无法切实地反映数据的真实机制[8-10]。灰色理论能弱化数据的随机性，忽略数据内部各要素间复杂和不明确的关系，利用其对灰色数据的记忆性挖掘数据，解决数据缺失、信息不完全等不稳定问题[11]，以多方面方法对数据进行预测。

1 研究方法

式(1)中：a称为发展灰数，反映X(0)(k)和X(0)(k)的发展趋势；b为控制灰数，体现数据间的内在联系与变化关系，均为待估参数项。

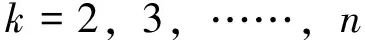
(1)

利用最小二乘法求解式(1)可得

(2)

求得a和b，再求解微分方程，得到

(3)

将式(3)离散化，可得

(4)

(5)

带入式(4)中

(6)

对上式作累减还原，得

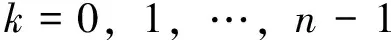
(7)

2 实例研究

2.1 基本资料

河南省位于中国中东部、黄河中下游，介于东经110°21′～116°39′和北纬31°23′～36°22′之间，横跨黄河、海河、淮河、长江四大水系，属于亚热带半湿润季风气候。2015年，河南省生产总值37 010.25亿元，比上年增长8.3%，人均生产总值39 222.39元。其中：第二产业增加值18 189.36亿元，增长8.0%，占河南省经济发展较大的比重。

本次试验所用的1998—2009年郑州对黄河取水量和工业取水量数据，均摘自《黄河水资源公报》。详见图1。

2.2 灰色理论模型实例

对原始数据进行级比检验,见表1。

表1 原始数据级比检验值

首先对原始数据序列进行1-AGO计算，得到累加算子序列X(1)(k)，以及其背景数值Z(1)(k)，具体数据见表2。

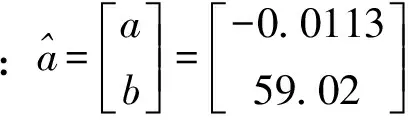
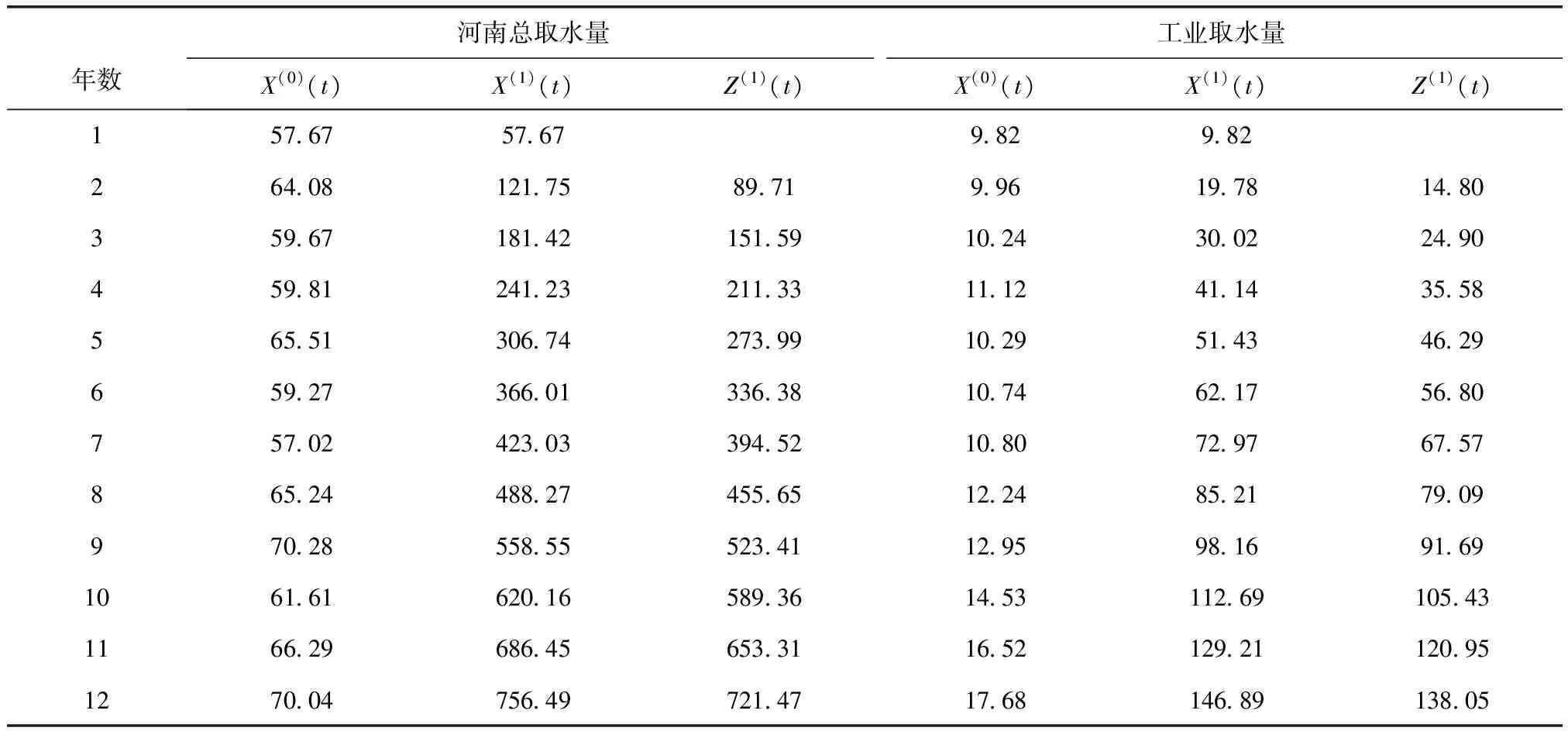
表2 模型参数表 亿m3

根据各个灰色理论模型，对原始数据进行拟合，具体数值见图2和表3。

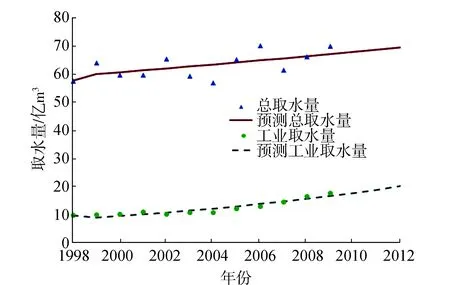
图2 原始数据与预测值对比图

亿m3

根据原始数据序列与灰色理论模型拟合的预测数据序列，反映出原始数据序列的趋势性、规律性，取得的效果较好；其中工业取水量的拟合程度更高。

2.3 精度检验

通过构建灰色理论模型GM(1，1)，弱化原始数据的随机性，得到的拟合值与原始数据相比数值较为接近，拟合效果显著。将预测后3 a的数据与原始数据进行误差分析和精度分析。

残差：

(8)

相对误差：

(9)

平均相对误差：

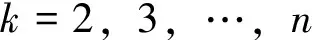
(10)

精度：

(11)

式(11)中：q(k)是残差值；ε(k)为相对误差；ε(avg)是平均相对误差；p为预测精度。

预测值误差分析见表4。

表4 预测值误差分析 亿m3

通过上述公式计算，预测2010—2012年河南省对黄河的总取水量和工业取水量，与《黄河水资源公报》上实际值相比较，总取水量的残差值在-2.14～-10.53之间，相对误差在3.05%～13.16%之间，平均相对误差7.01%，预测值的精度为92.99%；工业取水量的残差值在-0.29～2.24之间，相对误差在1.61%～12.53%之间，平均相对误差4.91%，预测值的精度为95.19%。两个模型整体拟合效果和预测效果较好，精度较高。

3 结 论

(1)根据灰色理论建立的灰色理论预测模型可用于非线性的波动性强的数据序列中，能揭示数据内在的规律，取得较好的预测结果。

(2)通过对1998—2009年河南省取黄河总水量和工业取水量数据的拟合，预测2010—2012年3 a的取水量；经过与实际数据相对比，模型拟合和预测精度较高，具有一定适用性。

(3)仅针对黄河流域沿线城市的取水量进行拟合和预测，可协助相关部门对黄河水资源的优化配置做出决策。

(4)城市对流域的取水量受多种因素影响，本文仅针对水资源公报数据进行建模，其他因素将是下一步研究的方向。

[1] 张吉辉. 天津市工业用水预测与节水潜力分析[D]. 天津: 天津理工大学, 2008.

[2] 彭少明, 郑小康, 王煜,等. 黄河典型河段水量水质一体化调配模型[J]. 水科学进展, 2016, 27(2):196-205.

[3] Dianep Dupont, Steven Renzetti. The Role of Water In Manufacturing [J]. Environmental And Resource Economics, 2001(18):411-432.

[4] Yano, Shinjiro, Hanasaki, et al. Water Scarcity Footprints by Considering the Differences in Water Sources[J]. Sustainability, 2015, 7(8):9753-9772.

[5] 褚桂红. 基于RBF神经网络的工业取水量预测研究[J]. 山西水利科技, 2011(2):9-11.

[6] 高珺, 赵娜, 高齐圣. 中国水资源供需模型及预测[J]. 统计与决策, 2014(1):85-87.

[7] 潘国强. 基于最小二乘支持向量机的万元工业GDP取水量非线性组合预测[J]. 水资源与水工程学报, 2013, 24(5):161-164.

[8] Bezuglov Antor, Comert Gurcan. Short-term freeway traffic parameter prediction: Application of grey system theory models [J]. Expert Systems with Applications, 2016(62):284，292.

[9] 马建琴, 许龙宾, 师琨. 改进型灰色马尔科夫模型在径流预测中的应用[J]. 华北水利水电学院学报, 2012, 33(2):39-42.

[10] 朱晓华, 杨秀春, 蔡运龙. 基于灰色系统理论的旅游客源预测模型—以中国入境旅游客源为例[J]. 经济地理, 2005, 25(2):232-235.

[11] Trivedi H V. Singh J K. Application of grey system theory in the development of a runoff prediction model[J]. Bio-systems Engineering, 2005, 9(4):521-526.

Study on city water intake quantity of river basin based on Grey Theory

ZHANG Chengquan

(AnshanHydrologyBureau,Zhengzhou114039,China)

The city water intake quantity of river basin is uncertain and random, which includes grey character. The industrial water intake quantity of river basin has more grey information. It's difficult to make a visual, qualitative and quantitative prediction for the complex and fuzzy stochastic processes by conventional mathematical methods. Grey information is a special information between white information and black information. Grey theory can reveal the grey and randomness of information, analyze and process the data to generate highly regular numerical sequence by screening the different degree of internal development trend of information. Then the grey system model is established to predict the development trend of the data. Based on grey theory and grey prediction, the grey of original data is revealed, the grey theory model GM (1, 1) is constructed by level ratio test and accumulation operator. The model is applied to predict total water intake and industrial water intake of the Yellow River in Henan Province. The results show that the grey theory model has the advantage of strong maneuverability and high combination of theory and practice,can optimize the model results in a sequence of data shortages. The prediction of water consumption of the Yellow River in Henan Province though the model is with high accuracy, the relative error of total water intake is between 3.05%～13.16%, the relative error of industrial water intake is between 1.61%～12.53%. It provides theoretical reference for the unified scheduling and optimal allocation of the Yellow River water resources.

grey theory; GM (1, 1); water intake quantity; Henan

张承全(1984-)，男，工程师,主要从事水利工程施工和研究工作。

F224；TV213

A

2096-0506(2016)12-0045-05