国内外导线张力设计方法的差异

朱映洁，林方新

(中国能源建设集团广东省电力设计研究院有限公司，广东 广州 510663)



国内外导线张力设计方法的差异

朱映洁，林方新

(中国能源建设集团广东省电力设计研究院有限公司，广东 广州 510663)

摘要：我国输电线路设计规范在计算导线张力时未考虑自然风脉动的影响，因而采用较大的安全系数来抵抗风速脉动峰值引起的过载；而国外标准采用极限张力设计方法，计算导线张力时充分考虑自然风脉动的影响，因而采用较小的安全系数使允许的最大使用张力接近塑性变形临界值。这是造成我国导线计算张力与国外计算值相差较大的主要原因，也是国内输电线路设计体系与国外标准极限张力设计方法的一个显著区别。以实例计算的方式剖析了这两种不同的方法给铁塔设计带来的影响。计算结果表明，随着代表档距的增加，按国外标准计算的大风工况张力的上升坡度明显大于我国标准。在年平工况作为控制工况的前提下，极限张力设计法不会引起导线弧垂差异，并且按照极限张力设计法设计的耐张塔可承受更大的全相不平衡张力。

关键词：极限张力设计法；自然风脉动；风振系数；单位长度风荷载；不平衡张力

我国现行导线荷载计算体系源自前苏联规范，主要特点是：导线风荷载对自然风脉动影响考虑不足，正常工况下弧垂最低点最大使用张力的安全系数不小于2.5，并将稀有风速、稀有覆冰列为验算工况，要求在该工况下弧垂最低点的最大张力不超过拉断力的70%[1](GB 50790—2013《±800 kV直流架空输电线路设计规范》[2]要求不超过拉断力的60%)。这种设计方法采用较大的安全系数来抵抗瞬时风速的过载，因此也可以理解为：对于10 min平均风速不大于基本风速的自然风，如果由脉动引起的导致电线系统响应的瞬时风速不超出导线60%～70%拉断力所对应的稀有风速时，则导线不会进入塑性变形。

国外各主要输电线路设计标准几乎均考虑了脉动对导线风荷载的影响，因此设计时导线最大使用张力普遍比我国大，且安全系数的设置接近导线的塑性变形临界值，可视为极限张力设计法。

1不同标准对导线使用张力的规定

世界上各主要输电线路设计标准[1-6]对导线年平张力及最大使用张力的规定见表1。

表1导线张力的差异

标准导线年平张力导线最大使用张力国标0.25σn正常工况时:0.40σn;稀有风速、稀有覆冰时:0.70σn(110～750kV),0.60σn(±800kV)IEC标准无规定取以下值的最小值:振动限制;违反规程许可;0.75σm或0.75σnJEC标准0.30σn(铜系导地线)0.25σn(其他导地线)0.70σn(铜系导地线)0.60σn(其他导地线)ASCE标准初始空载张力0.35σn最终空载张力0.25σn0.70σn～0.80σnEN标准无规定无规定

注：σn为额定张力；σm为特性强度。

从表1可见，国外对导线最大使用张力安全系数的设定与我国稀有风、稀有覆冰时的安全系数是相当的，但这并不意味着国外标准是采用稀有风速或稀有覆冰来进行设计。

尽管国标、JEC标准[4]与ASCE标准[5]将年平均张力的上限定为额定张力的25%，但海外工程中较为通用的做法是取20%。

2不同标准对张力计算方法的规定

2.1计算高度

我国在计算普通单、双回线路的导线张力特性时，一般假设500 kV线路导线平均高度为离地20 m，110～220 kV线路导线平均高度为离地15 m。这是在导线对地最小安全距离的基础上确定的，因此也可被认为是下导线的平均高度。为方便施工放线，不同层的导线通常按同一张力来展放，因此不同层的导线张力也通常按同一高度来计算。实际上随着风速的增大，中层或上层导线张力超过下层导线计算张力的部分也被考虑在安全系数的裕度之中。

国外标准为方便计算，通常推荐采用导地线挂点高度进行张力计算。各主要标准对于计算高度的规定见表2。

表2计算导线张力时的导线高度差异

标准计算导线张力时的导线高度国标20m(500kV),15m(110～220kV)IEC标准高度z可认为是悬挂导线重心的高度,理论上比导线挂点低弧垂的三分之一。为了输电线路杆塔的计算,可以认为z等于导线在杆塔挂点的高度(对于导线水平的线路)或者中间导线的挂点高度(对于双回路线路)。这些假设是偏保守的,也是对塔顶地线造成高度增加的补偿ASCE标准有效高度理论上为地面以上风荷载中心的高度。有效高度主要用于计算风压高度系数和阵风响应因子。导线和地线的有效高度容易遭受风或风冰结合的影响,因为电线和绝缘子串在这种情况下左右摇摆。然而,出于结构设计的目的,所有导地线的有效高度可近似地取其悬挂点的平均高度EN标准计算高度应由各国定义。如果各国没有定义,通常可采用60m

按悬挂点计算导线张力，成为大部分海外工程的计算惯例。这比我国的常规做法更为保守，因为悬挂点必然高于导线平均高度，而对直线塔而言，中层横担的悬挂点高度也接近于上导线的平均高度。

国外标准对于导地线计算高度的规定契合了极限张力设计法的特点。如果不采用相对保守的数值来进行张力计算，则在最大风速下，上层导线的张力可能会超过设计张力，使导线进入塑性变形。

2.2单位长度风荷载、风振系数及张力计算

2.2.1单位长度风荷载计算

2.2.1.1国标

国标的单位长度风荷载计算方法为

g4=αWoμzμscd×10-3.

(1)

式中：g4为导线单位长度风荷载(无冰)，N/m；α为风压不均匀系数；Wo为基准风压标准值(基准高度为10 m)，kPa；μz为导线平均高度处的风压高度变化系数；μsc为导地线体型系数；d为导地线的外径或覆冰时的计算外径，m。

2.2.1.2IEC标准

IEC标准的单位长度风荷载计算方法为

g4=q0CxcGc1GLd.

(2)

式中：q0为动态参考风压，Pa；Cxc为导线阻尼系数；Gc1为风对导线的综合影响因数，其值取决于高度z和地形情况；GL为档距因数；d为导地线直径，m。

2.2.1.3ASCE标准

ASCE标准的单位长度风荷载计算方法为

g4=γwQKzKzt(V50)2GCfd.

(3)

式中：γw为荷载因子；Q为空气密度常数，表示将空气动能转化为压力的系数；Kz为风压高度系数；Kzt为地形影响因子；V50为基本风速(50年重现期，3 s阵风)，m/s；Cf为阻尼系数(体型系数)；d为导地线直径，m ；G为阵风响应因子。

(4)

式中：E为与平均风幂指数αFM、表面阻力系数k和导线有效高度zh有关的表达式；Bw为与水平档距S和湍流积分尺度Ls有关的表达式；Kv为3 s瞬时风速与10 min平均风速比值。

2.2.1.4EN标准

EN标准的单位长度风荷载计算方法为

g4=qp(h)Gc2Ccd.

(5)

式中：qp(h)为参考高度h处的基本风压(风压峰值，即瞬时风压)，Pa；Cc为阻尼系数(体型系数)；d为导地线直径，m；Gc2为结构因子。

(6)

2.2.2风振系数计算

从2.2.1可见，ASCE标准的阵风响应因子G和EN标准的结构因子Gc2采用结构相同的表达式。其中分母部分均为瞬时风压和10 min平均风压的比值，意为将输入的瞬时风压转换为10 min平均风压，而分子部分类似于GB 50009—2012《建筑结构荷载规范》[7]中风振系数的表达式，如式(7)所示。

(7)

式中：βz为风振系数；g为峰值因子；I10为10 m高度名义湍流度；Bz为脉动风荷载的背景分量因子；R为脉动风荷载的共振分量因子。

从ASCE标准阵风响应因子G和EN标准结构因子Gc2表达式中各项系数的定义也可以看出，其分子部分的实际意义即为在10 min平均风压基础上，考虑了自然风脉动效应的风振系数。

对式(4)稍作转化，ASCE标准风振系数计算表达式如下：

(8)

同样地，对式(6)稍作转化，EN标准风振系数计算表达式如下：

(9)

IEC标准使用以下公式计算综合影响因数Gc1和档距因数GL：

地形等级A，Gc1=0.291 4×ln(x)+1.046 8.

(10)

地形等级B，Gc1=0.373 3×ln(x)+0.976 2.

(11)

地形等级C，Gc1=0.493 6×ln(x)+0.912 4.

(12)

地形等级D，Gc1=0.615 3×ln(x)+0.814 4.

(13)

GL=4×10-10L3-5×10-7L2-10-10L+1.040 3.

(14)

式(10)—(14)中：x为离地高度；L为档距。

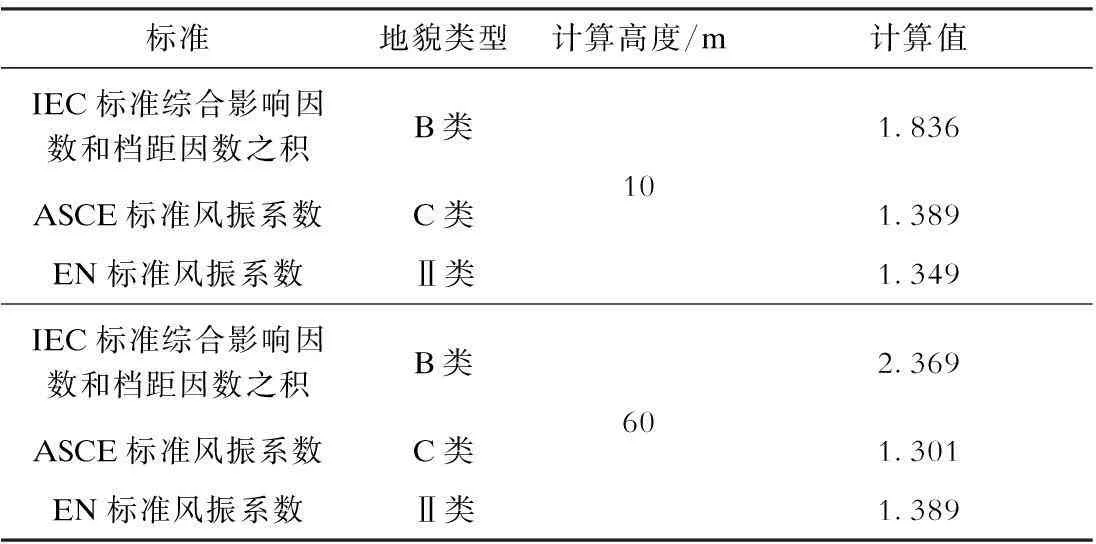
IEC标准虽然未定义与风振系数类似的表达式，但定义了与高度相关的系数Gc1和档距相关的系数GL。在输电线路设计时常用的典型地貌条件下(开阔地带，少量树木和建筑物)，IEC标准综合影响因数和档距因数之积Gc1·GL与其他标准风振系数计算值比较见表3。

表3IEC标准综合影响因数和档距因数之积与其他标准风振系数计算值

标准地貌类型计算高度/m计算值IEC标准综合影响因数和档距因数之积ASCE标准风振系数EN标准风振系数B类C类Ⅱ类101.8361.3891.349IEC标准综合影响因数和档距因数之积ASCE标准风振系数EN标准风振系数B类C类Ⅱ类602.3691.3011.389

注：1.水平档距400 m。2.我国的风振系数计算方法并不适用于跨度远大于两倍铁塔高度的导线系统[7-8]，同时在导地线风压尤其是在单位长度风荷载计算中也并未使用这一系数，因此本表不予计算。

考虑到IEC标准中的q0即指离地10 m处的基准风压，且除Gc1外，风荷载计算公式中没有其他进行高度换算的系数，因此推断Gc1与GL的乘积从理论意义上来说还应包含了风压高度变化系数。但从表3可见，即便在10 m高度处，综合影响因数Gc1和档距因数GL的乘积也远大于其他标准的风振系数值，说明IEC标准对基于10 min平均风压的脉动特性已经考虑充足。文献[9]绘制了不同标准下的风振系数对比曲线，也反映了这一特征。

2.2.3导线张力计算

虽然GB 50009—2012《建筑结构荷载规范》定义了风振系数，但提出该系数的计算方法仅适用于结构迎风面宽度不大于2倍结构高度的系统[7]；根据《电力工程高压送电线路设计手册》[10]，我国输电线路设计方法在导线单位长度风荷载计算中也并未使用类似系数，这是造成我国导线计算张力与国外计算值相差较大的主要原因，也是国内输电线路设计体系与国外标准的一个显著区别。此外，我国在计算500 kV及以上电压等级线路导线风荷载时，根据风速的划分区间使用了不同的导线风荷载调整系数[1]，但该系数不进入特性计算，因此与各工况下的计算张力无关，而仅与铁塔所受导线荷载相关。

假设：年平工况气象条件为20 ℃，无风，无冰；大风工况气象条件为20 ℃，35 m/s(离地10 m高10 min平均风速)，无冰；高温工况气象条件为40 ℃，无风，无冰；导线型号为JL/G1A-630/45，直径33.8 mm，计算破断拉力150.45 kN；水平档距400 m。在输电线路设计时常用的典型地貌条件下(开阔地带，少量树木和建筑物)，用各标准计算所得的大风工况单位长度风荷载及导线张力见表4。

表4单位长度风荷载及导线张力

标准单位长度风荷载/(N·m-1)代表档距/m导线张力/N年平工况大风工况高温工况国标IEC标准ASCE标准EN标准24.7259.7347.8845.2730035731.949803.430138.828585.5a71536.1a25199.2a35731.9b80874.1b30138.8b28585.5a61525.1a25199.2a35731.9b70549.3b30138.8b28585.5a59275.5a25199.2a35731.9b68218.8b30138.8b国标IEC标准ASCE标准EN标准24.7259.7347.8845.2740035731.951816.931983.228585.5a76627.7a26428.7a35731.9b88277.0b31983.2b28585.5a65162.0a26428.7a35731.9b76071.5b31983.2b28585.5a62601.9a26428.7a35731.9b73326.4b31983.2b国标IEC标准ASCE标准EN标准24.7259.7347.8845.2750035731.953055.933084.228585.5a79858.7a27110.8a35731.9b93457.7b33084.2b28585.5a67389.4a27110.8a35731.9b79811.5b33084.2b28585.5a64621.2a27110.8a35731.9b76756.3b33084.2b国标IEC标准ASCE标准EN标准24.7259.7347.8845.2760035731.953852.833779.328585.5a81991.1a27520.8a35731.9b97156.6b33779.3b28585.5a68821.0a27520.8a35731.9b82407.7b33779.3b28585.5a65910.6a27520.8a35731.9b79120.4b33779.3b

注：1.国标导线平均高度按20 m计算，其他标准按60 m计算；2.国标按年平工况安全系数4.0计算，其他标准按年平工况安全系数分别按5.0(上标a)及4.0(上标b)两种情况计算。

图1对应表4中上标为a的大风工况张力数据，图2对应表4中上标为b的大风工况张力数据。

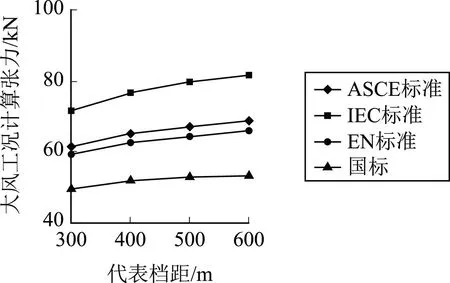
图1　大风工况导线计算张力比较(一)

图2　大风工况导线计算张力比较(二)

在假设的气象条件下，四种标准均为年平工况控制，因此在年平工况安全系数一致的情况下，年平工况的张力是一样的，而大风工况的张力各有不同，其中按IEC标准计算的大风工况张力最大，按我国标准计算的大风工况张力最小。

表4是在假设10 min平均风速一致的前提下进行计算的。在实际工程中，IEC标准建议230 kV以上电压等级线路选择重现期为150年的可靠性水平。对于230 kV以下电压等级但为网络中重要的组合部分或者是某负荷的唯一电源线路，同样也建议选择150年的可靠性水平。对于大部分230 kV以上电压等级，而且是网络重要的组合部分或者是某负荷的唯一电源的线路，应该选用重现期为500年的可靠性水平。而我国对500 kV线路一般采用50年重现期，对220 kV及以下线路采用30年重现期。ASCE标准及EN标准的基准重现期均为50年，但允许采用更高可靠度水平的重现期进行设计。因此采用国外标准设计的线路可能比我国标准具有更高的重现期水平，以致大风工况的单位长度风荷载和张力差异比表4中计算的更大。

另外值得注意的是，IEC标准提出：如果一个耐张段被悬垂绝缘子串分成几个部分，代表档距的概念就会用于张力计算。需要强调的是，代表档距的概念意味着一个耐张段所有档受到相同的风压。这种假定随档数的增加和悬垂串长度的增大而变得更保守。如果有经验和数据支持，在一些情况下计算的风荷载可以减小，但不会减小40%以上。当考虑到地线时，不宜减小风压，因为没有悬垂绝缘子串可阻止水平张力差的平衡(当采用接近40%的减少因数时务必谨慎，因为一些杆塔会被使用于较少档的耐张段，甚至是孤立档，这种情况下不能采用减少因数)。

这种考虑是有意义的，尤其对于较长的耐张段，不可能每个位置同时达到风速的脉动峰值。通过绝缘子串的偏转，可使得不同档的导线张力达到脉动折减后的平衡。但在国际通用输电线路设计软件PLS-CADD中，综合因数与档距系数均参与特性计算，且在特性计算的输入界面并无单位长度风荷载减小系数的设置项，因此该条可被认为在PLS-CADD中未得到应用。

2.3分项系数

各标准中，有关荷载的分项系数规定见表5。

表5分项系数对比

标准恒载分项系数活载分项系数国标1.21.4IEC标准1.01.0ASCE标准1.01.0EN标准1.01.0

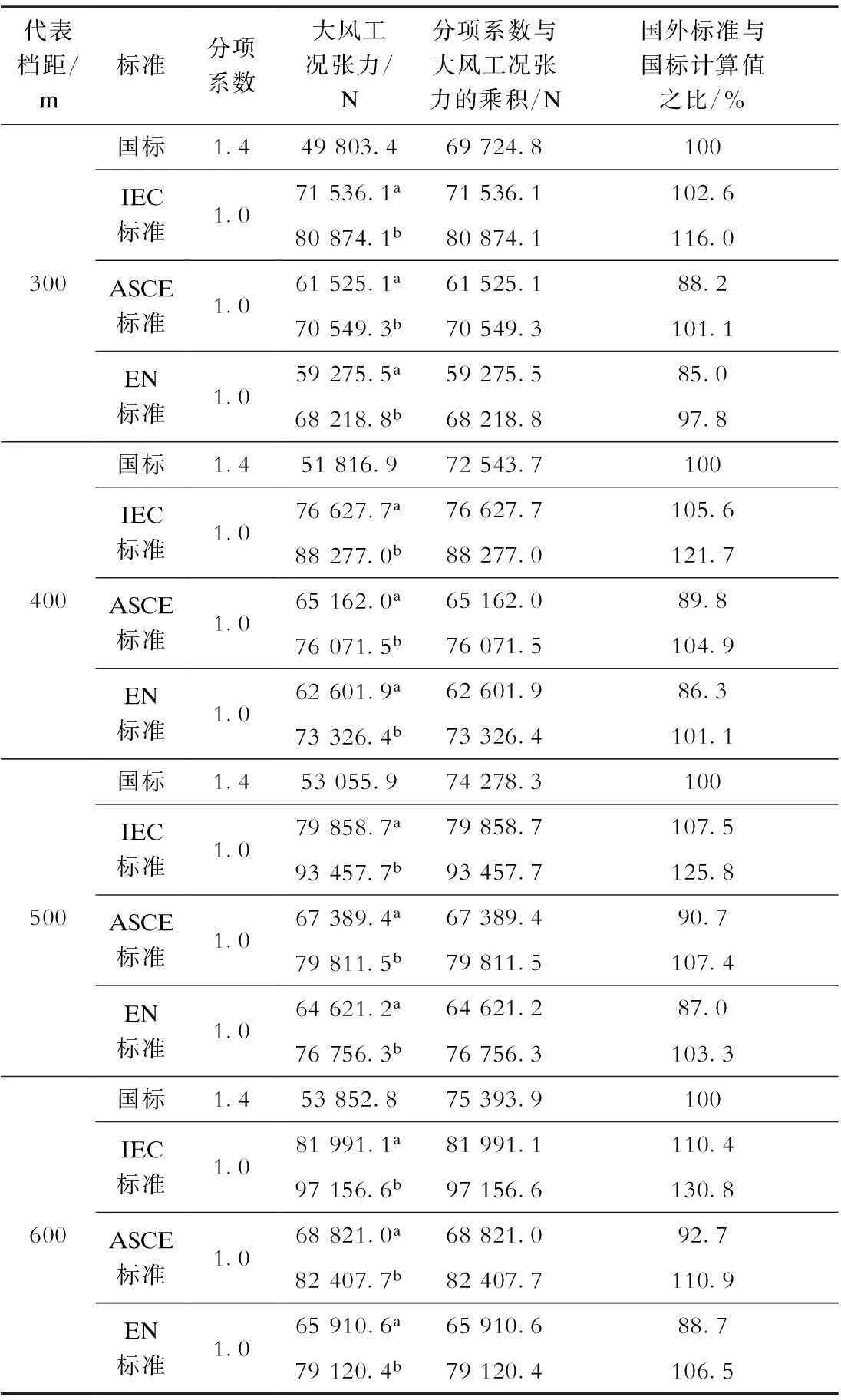
张力属于活荷载，因此在大风工况张力乘以分项系数之后，各标准在进行铁塔内力计算时实际使用的张力值见表6。

表6分项系数与大风工况张力之积

代表档距/m标准分项系数大风工况张力/N分项系数与大风工况张力的乘积/N国外标准与国标计算值之比/%300国标IEC标准ASCE标准EN标准1.41.01.01.049803.469724.810071536.1a71536.1102.680874.1b80874.1116.061525.1a61525.188.270549.3b70549.3101.159275.5a59275.585.068218.8b68218.897.8400国标IEC标准ASCE标准EN标准1.41.01.01.051816.972543.710076627.7a76627.7105.688277.0b88277.0121.765162.0a65162.089.876071.5b76071.5104.962601.9a62601.986.373326.4b73326.4101.1500国标IEC标准ASCE标准EN标准1.41.01.01.053055.974278.310079858.7a79858.7107.593457.7b93457.7125.867389.4a67389.490.779811.5b79811.5107.464621.2a64621.287.076756.3b76756.3103.3600国标IEC标准ASCE标准EN标准1.41.01.01.053852.875393.910081991.1a81991.1110.497156.6b97156.6130.868821.0a68821.092.782407.7b82407.7110.965910.6a65910.688.779120.4b79120.4106.5

注：1.国标导线平均高度按20 m计算，其他标准按60 m计算；

2.国标按年平工况安全系数4.0计算，其他标准按年平工况安全系数分别按5.0(上标a)及4.0(上标b)两种情况计算。

表7高温弧垂差异

标准高温工况张力/N弧垂/m国标31983.212.75IEC标准26428.7a15.4331983.2b12.75ASCE标准26428.7a15.4331983.2b12.75EN标准26428.7a15.4331983.2b12.75

注：1.国标导线平均高度按20 m计算，其他标准按60 m计算；

2.国标年平工况安全系数为4.0，其他标准年平工况安全系数分别按5.0(上标a)及4.0(上标b)两种情况计算。从表6可以看出，按我国标准计算的大风工况张力乘以分项系数之后，与ASCE标准和EN标准较为接近，但明显小于IEC标准。此外，随着代表档距的增加，按国外标准计算的大风工况张力的上升坡度明显大于我国标准，表现在表6的“比例”一栏数值随之上升。

表6的计算结果是建立在10 min平均风速相同的基础上。如果采用不同的气象重现期，不同标准之间计算张力的差异将会增大。

3计算张力对弧垂的影响

表4在假设条件下计算出了各个标准的高温工况张力。可据此进一步计算各标准的高温弧垂。以代表档距400 m为例，各标准的高温弧垂计算值见表7。

由于本文算例在各标准下均为年平工况控制，因此当年平张力安全系数一致时，高温工况的张力和弧垂也是一致的。仅当年平张力安全系数不一致时，才会出现弧垂的差异，但这并非由极限张力设计法引起的差异。

当设计风速足够大，使得大风工况成为控制工况后，规律将有所不同。

4计算张力对铁塔受力的影响

对于直线塔来说，由于绝缘子串的偏摆作用使得大风工况下的导线不平衡张力非常小，因此大风工况下计算张力的区别对塔重影响可以忽略不计。而对于耐张塔来说，大风工况下的计算张力决定了全相不平衡张力(即全部相导线同时产生的前后侧张力差)的大小，并直接对塔重产生影响。

假设耐张塔为0°转角，每相采用4分裂导线，前后侧代表档距分别为600 m及300 m。其他计算条件与表4一致。各标准下的导线每相不平衡张力计算值见表8。

表8耐张塔每相不平衡张力

标准代表档距/m分项系数大风工况单根导线张力/N乘积/N每相不平衡张力/N国标6003001.453852.849803.475393.969724.822676.4IEC标准6003006003001.081991.1a71536.1a97156.6b80874.1b81991.171536.197156.680874.141820.065130.0ASCE标准6003006003001.068821.0a61525.1a82407.7b70549.3b68821.061525.182407.770549.329183.647433.6EN标准6003006003001.065910.6a59275.5a79120.4b68218.8b65910.659275.579120.468218.826540.443606.4

注：1.国标导线平均高度按20 m计算，其他标准按60 m计算；

2.国标年平工况安全系数为4.0，其他标准年平工况安全系数分别按5.0(上标a)及4.0(上标b)两种情况计算。

由于按国外标准计算的大风工况张力随代表档距增加而上升的坡度明显大于我国标准，其作用于耐张塔上的每相导线不平衡张力也大于我国标准，因此可以得出结论：按照极限张力设计法设计的耐张塔可承受更大的全相不平衡张力。但不能据此判断按国外标准设计的耐张塔塔重比我国更大，因为耐张塔受力计算还受到大风工况水平荷载、事故工况任意相不平衡张力、安装工况荷载等其他因素控制，更受到有关结构设计不同标准差异的影响。

5结论

a)我国在单位长度风荷载计算中并未使用风振系数，这是造成我国导线大风工况计算张力与国外计算值相差较大的主要原因，也是国内输电线路设计体系与国外标准的一个显著区别。

b)在相同重现期及风速条件下，按我国标准计算的大风工况张力乘以分项系数之后，与ASCE标准与EN标准较为接近，但明显小于IEC标准。而国外实际工程设计所使用的重现期可能远大于我国。

c)随着代表档距的增加，按国外标准计算的大风工况张力的上升坡度明显大于我国标准。

d)在年平工况作为控制工况前提下，极限张力设计法不会引起导线弧垂差异。

e)按照极限张力设计法设计的耐张塔可承受更大的全相不平衡张力。

参考文献：

[1] GB 50545—2010，110 kV～750 kV架空输电线路设计规范[S].

[2] GB 50790—2013，±800 kV直流架空输电线路设计规范[S].

[3] CEI/IEC 60826，Design Criteria of Overhead Transmission Lines[S].

[4] JEC-127-1979，JEC送电用杆塔设计标准[S].

[5] ASCE Manuals and Reports on Engineering Practice No.74，Guidelines for Electrical Transmission Line Structural Loading(Third Edition)[S].

[6] BS EN 50341-1：2012，Overhead Electrical Lines Exceeding AC 45 kV[S].

[7] GB 50009—2012，建筑结构荷载规范[S].

[8] 张相庭. 结构风工程理论·规范·实践[M]. 北京：中国建筑工业出版社，2006：99-119.

[9] 屈讼昭. 国内外输电塔风荷载技术标准比较分析[J]. 电力建设，2013，34(5)：22-29.

QU Songzhao. Comparative Analysis of Wind Load Technical Standard on Power Transmission Tower Between China and Foreign Countries，2013，34(5)：22-29.

[10] 张殿生. 电力工程高压送电线路设计手册[M]. 2版. 北京：中国电力出版社，2003：179-181.

朱映洁(1981)，女，湖南邵阳人。工程师，工学硕士，从事超高压送电线路设计工作。

林方新(1973)，男，广东阳江人。高级工程师，工学学士，从事超高压送电线路设计和评审工作。

(编辑彭艳)

Differences of Design Methods for Domestic and Overseas Conductor Tension

ZHU Yingjie, LIN Fangxin

(China Energy Engineering Group Guangdong Electric Power Design Institute Co., Ltd., Guangzhou, Guangdong 510663, China)

Abstract：Influence of natural wind fluctuation is not considered for calculating conductor tension in design specifications on power transmission line in China, thereby, large safety factor is used to resist overload caused by peak value of wind speed fluctuation. While in foreign standard, ultimate tension design method fully considering influence of natural wind fluctuation is used to calculate conductor tension, thus small safety factor is adopted to make allowed maximum working strength close to critical value of plastic deformation. Above circumstances are main reasons for causing large differences between calculated values of conductor tension in domestic and overseas, as well as design methods for design system of power transmission line in China and foreign standard ultimate tension. Example calculation is used for analyzing influences on design for steel tower by using these two different methods and results indicate that with increase of ruling span, rising slope of tension under extreme wind condition calculated according to foreign standard is obviously larger than that according to domestic standard. On the premise of taking yearly average working condition as the controlling working condition, ultimate tension design method will not cause difference of conductor sag and tension support tower designed based on ultimate tension design method can bear greater whole-phase imbalance tension.

Key words：ultimate tension design method; natural wind fluctuation; wind vibration factor; per unit length of wind load; imbalance tension

作者简介：

中图分类号：TM756.2

文献标志码：A

文章编号：1007-290X(2016)01-0124-07

doi:10.3969/j.issn.1007-290X.2016.01.024

收稿日期：2015-08-19