基于改进经验模态分解和谱峭度法的变压器振动故障特征提取
2016-03-01陈东毅陈杰辰李冲
陈东毅,陈杰辰,李冲
(1.福州大学 电气工程与自动化学院,福建 福州350116;2. 福建省电力有限公司三明供电公司,福建 三明365000)

基于改进经验模态分解和谱峭度法的变压器振动故障特征提取
陈东毅1,陈杰辰2,李冲2
(1.福州大学 电气工程与自动化学院,福建 福州350116;2. 福建省电力有限公司三明供电公司,福建 三明365000)
摘要:针对变压器振动故障信号易被强背景噪声掩盖的特点,提出基于改进经验模态分解(empirical mode decomposition, EMD)与谱峭度法的变压器振动故障特征提取方法。首先利用EMD方法分解原振动故障信号得到一系列本征模态函数(intrinsic mode function,IMF)分量后,采用能量矩占比和方差贡献率相结合的方法对采样信号进行EMD降噪处理,消除EMD中的虚假分量;然后利用重构算法提取真实IMF分量,运用谱峭度法提取振动故障特征频率;最后以模拟工程实际信号为例,采用MATLAB仿真验证了该变压器振动故障特征提取方法的有效性。
关键词:改进经验模态分解;谱峭度;振动信号;故障特征提取
变压器状况变化会直接影响到电力系统的稳定性[1]。长期带负荷运行的变压器,一直工作在恶劣的环境中,处于亚健康状态,因此需要对变压器的健康状况进行实时监测与评价。变压器铁心及绕组故障是主要影响其健康状况的原因之一[2-4],故障引起的变压器器身表面振动信号异常为在线监测变压器提供了方法,但如何准确提取振动信号中的故障特征成为变压器故障诊断的关键。
振动信号具有暂态、突变等非平稳随机的特点[5],为了能够得到准确表征故障的特征频率,本文应用希尔伯特-黄变换(Hilbert-H transform,HHT)对振动信号进行有效分析,通过经验模态分解(empirical mode decomposition,EMD)方法将故障振动信号分解为一系列互相独立的本征模态函数(intrinsic mode function,IMF)分量。包含信号局部特性的IMF分量含有原始信号的重要信息,表征了信号的内在特征,更加有利于提取机械振动信号特征参数[6-8]。
传统EMD由于自身分解规则的缺陷,其分解结果中存在虚假IMF分量,尤其低频虚假IMF分量[9-11],会对故障特征信号的提取分析与处理造成较大的影响。由于振动信号具有典型的非高斯分布特征[12],零均值、零时滞的四阶累积量即峭度对非高斯信号非常敏感,能有效描述信号偏离高斯分布的程度[13]。本文提出基于改进EMD和谱峭度算法的变压器故障特征提取方法,首先将能量矩占比和方差贡献率对采样信号进行EMD降噪,消除EMD中的虚假分量;利用重构算法提取真实IMF分量,通过谱峭度原理确定带通滤波器参数,对降噪后信号包络解调分析进行变压器故障特征提取;最后以模拟工程实际信号为例进行验证。
1基于能量矩占比和方差贡献率的改进EMD
将一个时间序列信号经过EMD为不同尺度的IMF分量,再将某些IMF分量进行组合,以构造高通、低通、带通滤波器[14]。但对于电力变压器而言,由于其与故障有关的振动信号成分通常处于较低频段,故可以通过IMF的相关组合进行降噪处理,将EMD得到的高频分量作为噪声直接去除;此外,EMD自身的分解规则缺陷会存在虚假IMF分量,影响故障的诊断。为此,本文提出对IMF分量进行一定的组合,并根据以下两个原则选取有用的IMF分量。
a)原则一,各阶IMF能量矩占比[15]。经过EMD得到的信号通常会有虚假IMF分量,其与原始信号无关但所包含的频率成分可能会与特征频率重叠,因此需要从虚假分量中筛选出有用的信号。本文提出通过计算各阶IMF分量,求得其能量矩在原始信号能量的占比,来筛选有用的IMF分量的方法。IMF能量矩考虑到IMF能量的大小以及其随时间参数的分布情况,能更好表征能量分布;同时,若能量矩占比表达出几阶的能量矩所占总能量的比例均较大,则其越能反映出原始信号的能量情况,包含的有用信息越丰富,进而选取出有用的IMF分量。
利用式(1)求出各阶IMF能量矩E,并形成包含各阶IMF能量相对于原始信号能量矩占比向量T。

(1)
式中:cj(t)为IMF分量;Ei为各阶IMF分量的能量矩;Δt为采样周期;n为总的采样点数;k为采样点。
b)原则二,方差贡献率是用来表征各信号成分的相对重要程度。为了准确获得有用的IMF分量,对分解得到的每个IMF分量进行方差贡献率计算,从而确定IMF分量。计算公式可表述为
(2)
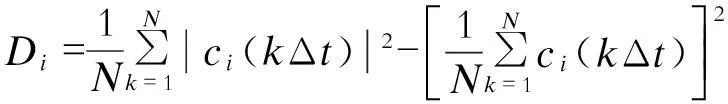
式中:ci为第i个IMF分量;Di为第i个IMF分量的方差;Mi为相应的方差贡献率;N为采样点数。
Mi越大,说明分解后的各IMF分量相较于原始信号越重要且越不能消除;反之则说明IMF分量相较于原始信号并不重要[16]。
2谱峭度法
本文首先采用改进EMD对原信号进行预处理,经过EMD降噪后消除了EMD分解中的虚假分量,得到在背景噪声被有效滤除的检测环境中的重构信号。因此,可以通过峭度利用奇异信号强敏感性特点识别出检测系统中的异常信号,但还是无法充分反映特定信号的变化情况。为了克服峭度的不足,Dwyer最早提出谱峭度法,谱峭度作为一个频域统计工具对信号中的非高斯成分进行度量,有效解决了提取信号中瞬态现象的问题。也就是,谱峭度法能够对强噪声背景中瞬态冲击成分进行有效的分析与定位[17-19]。
文献[20]对谱峭度进行深入研究,基于四阶谱累积量给出了谱峭度的正式定义,并将其成功应用于实际机械故障诊断中。针对CNS(conditionally nonstationary)过程中非平稳信号x(t)的四阶谱累积量的谱峭度定义为:

(3)
式中:S2nX(t,f)为2n阶瞬时矩,是复包络能量的度量,下标X表示信号x(t)由时域分量转换为频域分量。
将信号x(t)的谱峭度定义为能量归一化累积量,即
(4)
式中KX(f)为信号x(t)的谱峭度。
谱峭度具有诸多特性[17],根据式(4)可知,对于一个条件非平稳随机信号Z(t)=x(t)+N(t),N(t)为独立于x(t)的噪声信号,则信号Z(t)的谱峭度
(5)
式中:KN(f)为噪声N(t)的谱峭度;ρ(f)为噪信比,ρ(f)=S2N(f)/S2X(f)。
分析式(5)可知,当N(t)为加性白噪声时,ρ(f)越大,KZ(f)越接近0;相反,ρ(f)越小,则KZ(f)近似等于KX(f)。因此,谱峭度最大的频带即x(t)所在的频带,可以通过计算整个频域的谱峭度得到[18]。
3变压器振动特征提取算法
谱峭度法虽然能够提取变压器振动信号中的特征频率,但若是对原始振动信号进行一定的预处理,则可以更进一步提高诊断的准确性。如文献[14]采用EMD降噪技术对原始信号降噪,文献[19]采用改进的EMD和谱峭度法对原始信号进行预处理,均取得不错的特征提取效果。本文在上述文献的基础上,针对EMD中存在虚假IMF分量的问题,提出采用能量矩占比和方差贡献率相结合的方法,对振动信号进行降噪处理与重构,计算重构信号的谱峭度,从而得到快速谱峭度图上的中心频率和带宽,并以此构造带通滤波器对重构后的信号进行包络解调分析。
图1为基于改进EMD和谱峭度法的变压器故障特征频率提取的流程,具体特征提取的步骤如下:
a)对变压器振动信号进行EMD;
b)计算原始振动信号与各阶IMF分量的能量矩占比以及方差贡献率;
c)选取能量矩占比和方差贡献率均较大所对应的IMF分量来重构原始振动信号;
d)验证重构后的信号能够保留原始信号特征并进行降噪处理;
e)计算重构信号的谱峭度,选取图中谱峭度最大处所对应的中心频率与带宽;
f)构造以该中心频率和带宽为参数的带通滤波器,并对重构后的信号进行带通滤波;
g)计算重构信号经过滤波处理后的包络谱,从而提取振动信号特征频率。
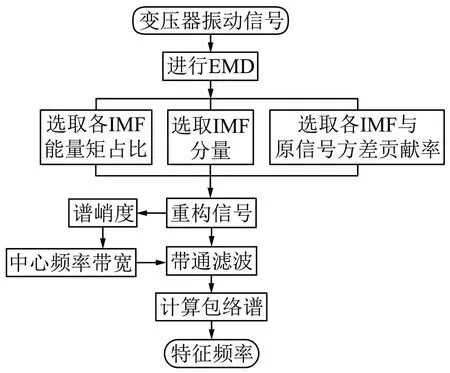
图1 变压器振动信号特征频率提取流程
4实验研究
为了验证本文提出的研究方法在变压器故障特征提取中的有效性,在MATLAB仿真实验平台中,依据实际变压器器身振动信号的物理特征进行振动信号模拟,仿真实验过程中总采样率为12 kS/s。文献[2-4]中提到的变压器绕组与铁心振动的特征频率主要集中在100 Hz及其倍数频率上,大致分布在200 Hz、300 Hz、400 Hz位置。图2给出了实验模拟变压器器身振动信号的时域波形及其频谱,从振动频域波形中可以得出特征频率点,说明此模拟振动信号可以合理的作为实际采集到的变压器器身振动信号。

图2 变压器振动信号时域波形及其频谱曲线
为提取变压器振动信号的特征频率,首先采用改进的EMD方法对振动信号进行分解,得到6个IMF分量。为了得到有用的IMF分量并且消除多余的虚假IMF分量,通过计算各阶IMF分量与原始信号的能量矩占比Ti和方差贡献率,以判定有用的IMF分量,结果见表1。
表1IMF分量与原始信号的Ti和Mi

分量名称Ti/%Mi/%分量名称Ti/%Mi/%IMF135.566535.45IMF42.44052.87IMF222.117123.56IMF50.51100.61IMF36.78697.29IMF60.27790.32
由表1可知,分量IMF1、IMF2、IMF3、IMF4与原始信号的相关程度较高,所包含信息最重要,IMF5、IMF6可以认为是虚假分量而被消除。图3给出了分量IMF1、IMF2、IMF3、IMF4的时域波形及其频谱分量,从中可以看到信号振动的特征。
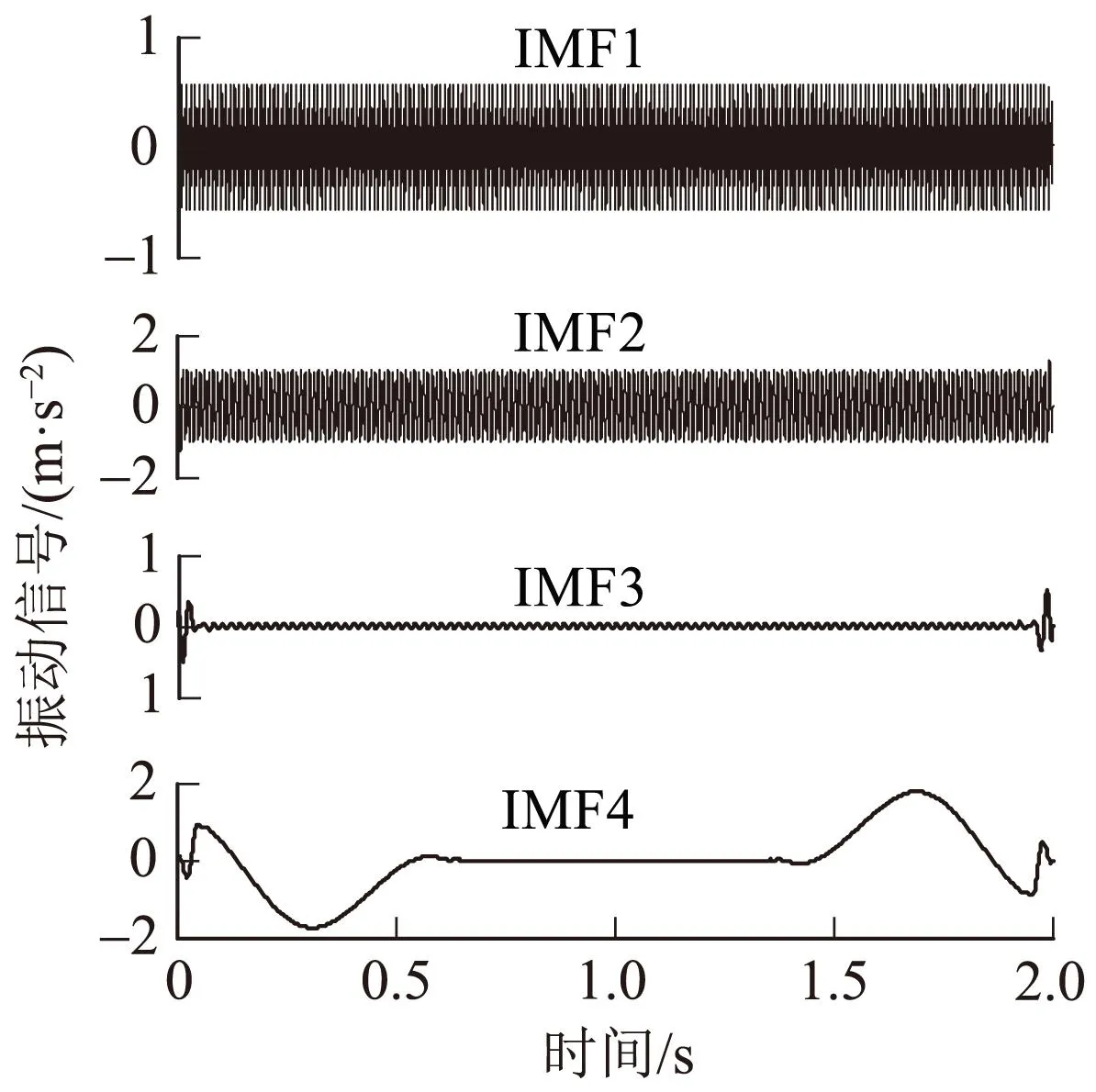
(a)时域

(b)频谱图3 IMF1—IMF4的时域波形及其频谱
对分量IMF1、IMF2、IMF3、IMF4进行重构,重构后的信号与原信号进行对比分析,得到重构信号与原始信号的误差,如图4所示。由于与故障有关的振动信号成分通常处于较低频段,重构后的信号将EMD分解得到的高频分量作为噪声直接去除。由图3、4可知,消除虚假IMF分量重构后的信号能代替原始信号,因此可以通过IMF的相关组合进行降噪处理,并滤除高频分量。
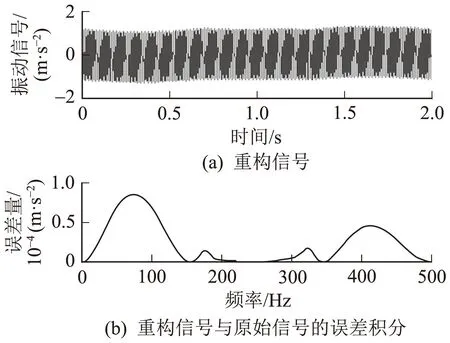
图4 重构信号及其与原始信号的误差
本文提出的方法对原始振动信号进行EMD降噪与重构,从而消除高频噪声,降低了低频干扰的影响,有效地提高了所要分析信号的谱峭度。其快速谱峭度如图5所示,带通滤波器中心频率约2 539 Hz,带宽为1 000 Hz,即频带[1539,3539]范围内的谱峭度最大,信噪比最大。

图5 快速谱峭度
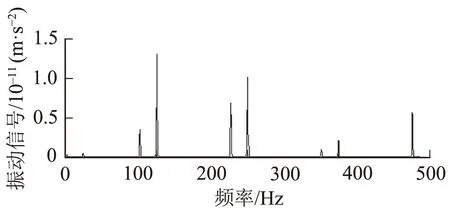
图6 信号滤波后的包络谱
带通滤波后的平方包络谱如图6所示,原始振动信号的特征频率为100 Hz,其倍数频率处均出现明显的特征谱线,表明本文所提方法可以准确提取变压器振动信号。
5结论
a)基于能量矩占比和方差贡献率的改进EMD方法能有效解决传统EMD分解会产生虚假分量的问题,采用EMD降噪处理并重构得到的IMF分量,能准确反映原始信号的特征信息。
b)谱峭度对隐藏在强噪声中的变压器振动冲击很敏感,可以借此确定带通滤波器的中心频率与带宽。
c)仿真实验验证了本文提出的新方法能够准确有效提取变压器故障特征频率,为变压器故障诊断研究提供了一个新的解决手段。
参考文献:
[1] 李军,董立文,赵红. 油浸式变压器的老化和寿命评估[J]. 高电压技术,2007,33(3):186-189.
LI Jun, DONG Liwen, ZHAO Hong. Aging and life Assessment of Oil-immersed Transformer [J].High Voltage Engineering, 2007, 33(3): 186-189.
[2] 汲胜昌,刘味果,李彦明,等. 振动法用于在线监测电力变压器绕组及铁心状况的可行性研究[J]. 高压电器,2001,37(5):4-7.
JI Shengchang, LIU Weiguo, LI Yanming, et al. Feasibility of Vibration Analysis Method in Application to On-line Monitoring of the Core and the Winding of Power Transformer[J]. High Voltage Apparatus, 2001, 37(5):4-7.
[3] 汲胜昌,刘味果,单平,等. 小波包分析在振动法监测变压器铁心及绕组状况中的应用[J].中国电机工程学报,2001, 21(12):24-27.
JI Shengchang, LIU Weiguo, SHAN Ping, et al. The Application of the Wavelet Packet to the Monitoring of the Core and Winding Condition of Transformer[J]. Proceedings of the CSEE, 2001, 21(12):24-27.
[4] 程锦,李延沐,汲胜昌,等. 振动法在线监测变压器绕组及铁心状况[J]. 高电压技术,2005,31(4):43-48.
CHENG Jin, LI Yanmu, JI Shengchang, et al. Application of Vibration Method on Monitoring the Winding and Core condition of Transforwer[J]. High Voltage Engineering, 2005, 31(4):43-48.
[5] 盖强,马孝江,殷福亮. 局域波多分辨分析及其在振动信号分析中的应用[J]. 仪器仪表学报,2006,27(6):1744-1745.
GAI Qiang, MA Xiaojiang, YIN Fuliang. Local Wave Multiresolution Analysis and Its Use in Vibration Signal Analysis[J]. Chinese Journal of Scientific Instrument, 2006, 27(6):1744-1745.
[6] HUANG N E, SHEN Z, LONG S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J]. Proceedings of the Royal Society of London Series A, 1998, 454(1971): 903-995.
[7] VINCENT H T. Damage Detection Using Empirical Mode Decomposition Method and A Comparison with Wavelet Analysis[C]//Structural Health Monitoring 2000. USA: Stanford, 2000:891-911.
[8] 张惠峰,马宏忠,陈凯,等.基于振动信号EMD-HHT 时频分析的变压器有载分接开关故障诊断[J].高压电器,2012,48(1):76-81
ZHANG Huifeng, MA Hongzhong, CHEN Kai, et al. Fault Diagnosis of Power Transformer On-load Tap Changer Based on EMD-HT Analysis of Vibration Signal[J]. High Voltage Apparatus, 2012, 48(1): 76-81.
[9] PENG Z K, PETER W T, CHU F L. An Improved Hilbert-huang Transform and Its Application in Vibration Signal Analysis[J]. Journal of Sound and Vibration, 2005(286): 187-205.
[10] WU Z H, HUANG N E. Ensemble Empirical Mode Decomposition-A Noise Assisted Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2009, 1(1):1-41.
[11] 彭畅,柏林,谢小亮. 基于EEMD、度量因子和快速峭度图的滚动轴承故障诊断方法[J]. 振动与冲击,2012,31(20):143-146.
PENG Chang, BO Lin, XIE Xiaoliang. Fault Diagnosis Method of Rolling Element Bearings Based on EEMD, Measure-factor and Fast Kurtogram[J].Journal of Vibration and Shock, 2012, 31(20):143-146.
[12] 林勇,周晓军,张文斌,等. 基于形态小波理论和双谱分析的滚动轴承故障诊断[J].浙江大学学报(工学版),2010,44(3):432-439.
LIN Yong, ZHOU Xiaojun, ZHANG Wenbin, et al. Rolling Bearing Fault Diagnosis Based on Morphological Wavelet Theory and Bi-spectrum Analysis[J]. Journal of Zhejiang University (Engineering Science), 2010, 44(3): 432-439.
[13] 邱天爽,张旭秀,李小兵,等. 统计信号处理:非高斯信号处理及应用[M].北京:电子工业出版社,2004.
[14] 苏文胜,王奉涛,张志新,等. EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J]. 振动与冲击,2010,29(3):18-21.
SU Wensheng, WANG Fengtao, ZHANG Zhixin, et al. Application of EMD Denoising and Spectral Kurtosis in Early Fault Diagnosis of Rolling Element Bearings[J]. Journal of Vibration and Shock, 2010, 29(3):18-21.
[15] 程军圣,罗颂荣,杨斌,等. LMD能量矩和变量预测模型模式识别在轴承故障智能诊断中的应用[J]. 振动工程学报,2013,26(5):751-757.
CHENG Junsheng, LUO Songrong, YANG Bin, et al. LMD Energy Moment and Variable Predictive Model Based Class Discriminate and Their Application in Intelligent Fault Diagnosis of Roller Bearing[J]. Journal of Vibration Engineering, 2013, 26(5):751-757.
[16] 姚刚,赵建军,姚跃亭,等. 基于改进EMD方法的系统误差分离方法研究[J].振动与冲击,2014,33(14):176-180.
YAO Gang, ZHAO Jianjun, YAO Yueting, et al. Separation of Systematic Error Based on Improved EMD Method[J]. Journal of Vibration and Shock, 2014, 33(14):176-180.
[17] ANTONI J. The Spectral Kurtosis of Nonstationary Signals: Formalization, Some Properties, and Application[C]//12thEuropean Signal Processing Conference. Vienna, Austria: [s. n.], 2004.
[18] 张志刚,石晓辉,施全,等. 基于改进EMD和谱峭度法滚动轴承故障特征提取[J].振动、测试与诊断,2013,33(3):478-482.
ZHANG Zhigang, SHI Xiaohui, SHI Quan, et al. Fault Feature Extraction of Rolling Element Bearing Based on Improved EMD and Spectral Kurtosis[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(3):478-482.
[19] 张志刚,石晓辉,陈哲明,等. 基于改进EMD与滑动峰态算法的滚动轴承故障特征提取[J]. 振动与冲击,2012, 31(22): 80-83.
ZHANG Zhigang, SHI Xiaohui, CHEN Zheming, et al. Fault Feature Extraction of Rolling Element Bearing Based on Improved EMD and Sliding Kurtosis Algorithm[J]. Journal of Vibration and Shock, 2012, 31(22): 80-83.
[20] ANTONI J. The Spectral Kurtosis: A Useful Tool for Characterizing Nonstationary Signals[J]. Mechanical Systems and Signal Processing, 2006(20): 382-407.

陈东毅(1987),男,福建福州人。助理实验师,工学硕士,主要研究方向为电力系统的检测与控制。
陈杰辰(1986),男,福建三明人。工程师,工学硕士,主要从事变电设备电气试验和状态在线监测管理工作。
李冲(1988),男,湖南岳阳人。助理工程师,工学学士,主要从事电力系统高电压技术工作。
(编辑钟美玲)
Transformer Vibration Fault Feature Extraction Based on Improved Empirical
Mode Decomposition and Spectral Kurtosis
CHEN Dongyi1, CHEN Jiechen2, LI Chong2
(1. College of Electrical and Engineering and Automation, Fuzhou University, Fuzhou, Fujian 350116, China; 2.Sanming Power Supply Company, Fujian Electric Power Company, Sanming, Fujian 365000, China)
Abstract:In allusion to the characteristic of transformer vibration fault signal being easy to be covered by strong background noise, a kind of transformer vibration fault feature extraction method based on improved empirical mode decomposition (EMD)and spectral kurtosis is proposed. Firstly, EMD method is used for decomposing original vibration fault signals and getting a series of intrinsic mode function (IMF)components, a combination method of using energy moment ratio and variance contribution is used for EMD denoising processing on sampling signals and eliminating false components in EMD. Then restricting algorithm is used for extract true IMF components and spectral kurtosis is used to extract vibration fault feature frequency. Finally, simulation on engineering practical signals is taken for an example and MATLAB simulation is used for verifying validity of this extraction method for transformer vibration fault feature.
Key words:improved empirical mode decomposition; spectral kurtosis; vibration signal; fault feature extraction
作者简介:
中图分类号:TM411;TN911
文献标志码:A
文章编号:1007-290X(2016)01-0011-06
doi:10.3969/j.issn.1007-290X.2016.01.003
收稿日期:2015-09-11修回日期:2015-10-20
