基于量子粒子群优化的油水井措施方案优选

孙 昊，李盼池

(东北石油大学计算机与信息技术学院，黑龙江大庆 163318)

基于量子粒子群优化的油水井措施方案优选

孙 昊，李盼池

(东北石油大学计算机与信息技术学院，黑龙江大庆 163318)

油水井措施方案优选是油田中后期开发面临的重要问题之一，目前主要依靠相关技术人员根据经验手工试算，不仅工作效率低而且往往不能得到最优结果。为解决这一问题，提出一种基于量子行为粒子群优化的解决方案。在深入研究现有的量子行为粒子群优化模型的基础上，利用量子力学原理考察了粒子在方势阱中的动态行为，进而提出一种新的量子行为粒子群优化算法。根据油田具体施工情况对油水井采取0-1编码，并综合考虑目标函数及各种措施组合必须满足的约束条件，合理构造适应度函数。在优化过程中，引入变异策略增加种群多样性。实验结果表明，该方法获得了令人满意的优化结果。

油水井施工方案;措施方案优选;量子粒子群优化;算法设计

1 概述

运用优化方法研究油田开发决策问题可追溯到1958年Aronofsky和Lee在JPT杂志上发表的题为《A Linear Programming Model for Scheduling Crude Oil Production》的文章。文章中运用线性规划方法研究了以生产效益最大为目标的有限多个均质油藏的生产规划问题。之后，又有几篇文章发表在MS/OR与JPT等刊物上，但在1985年以前，这些文章都属于探索性的，优化方法在油田开发决策中的应用还没有得到足够重视，因此在油田生产领域的成功应用仍然很少。1985年以后，由于油田开发的实际迫切需要和优化方法、计算机技术的迅速发展，情况有了很大变化。美国、前苏联和中国等主要产油国的一些科研单位、大专院校及石油公司都积极地使用优化技术研究各种各样的油田开发问题，在建模、求解和应用等方面都进行了较好的研究工作。

然而传统的优化技术均不同程度地存在缺陷，如单纯形法只适用于线性优化，神经网络法易于陷入局部极小值［1］，解析法需要建立精确的数学模型，等等。因此，应用智能优化算法解决油田工程问题正日益成为新兴的研究方向［2］。

已有理论证明，粒子群优化(Particle Swarm Optimization，PSO)是一种全局优化算法，具有种群规模小、收敛速度快、全局搜索能力强等优点［3-5］。任何实际问题，不论工程背景如何复杂，只要最终能够归结为求最小值和最大值问题，都可用PSO获得满意的解决方案［6］。PSO适用于一切优化问题，而与具体问题的工程背景无关，因而自1995年提出之后［7］，在各个工程领域很快获得了广泛的应用［8-11］。

油水井措施方案优化是指在综合考虑国家计划、资源条件、资金情况、措施种类、措施潜力、措施效果以及队伍、装备、矿场施工能力等因素的前提下，寻求一种为完成开发规划指令性任务，各项措施必须遵循的最优分配比例。措施方案优化是原油开发规划的核心之一，旨在统筹安排各种增产增注措施作业量，以最小的投人、最少的措施井次完成给定的油水井措施增产任务。油水井措施方案优选就是实现吨增油措施投入最低的非线性规划的极值问题，即根据油井和水井的各种措施单价，同时考虑总体方案的增油、增液、增注指标约束，以及各种措施施工井数的约束，合理安排一年中各个月份的措施施工井数，以使当年产出比和累计产出比最大。这实质上是一个带约束条件的最大值优化问题，即在满足增油、增液、增注等指标约束前提下，寻找一种施工方案，使施工效益最大化。抛开工程背景，该问题实质上就是一个连续优化问题，即一个多元函数求极值问题，解决该类问题，恰是粒子群优化的长处。

鉴于此，文中提出一种基于量子粒子群优化(Quantum Particle Swarm Optimization，QPSO)［12］的油水井措施方案优选方法，旨在为此问题的解决提供一种新途径。

2 PSO模型

2.1 基本PSO模型

设在n维空间中的M个粒子组成一个种群。其中，第i个粒子位置Xi、速度Vi、自身搜索到的最优位置、整个种群搜索到的最优位置Pg分别记为:Xi= (xi1，xi2，…，xin)，Vi=(vi1，vi2，…，vin)=(pi1，pi2，…，pin)，Pg=(pg1，pg2，…，pgn)。将Xi代入目标函数可计算其适应值。粒子更新策略为

其中，i=1，2，…，M;w为惯性因子;c1为自身因子;c2为全局因子;r1、r2是(0，1)之间的随机数。

对种群中每个粒子应用式(1)和式(2)循环迭代，可使整个种群逐步逼近全局最优解。

为便于叙述，将式(1)重写为如下形式［13］:

文献［14］指出，为使PSO收敛，所有粒子必须逼近式(4)定义的Pi。

2.2 量子PSO模型

在量子力学里，粒子动态行为一般用如下薛定谔方程描述。

其中，ħ为普朗克常数;m为粒子质量;V(r)为势场能量分布函数。

在薛定谔方程中，未知量是波函数Ψ(r，t)，根据波函数统计诠释，该函数幅度的平方表示粒子t时刻在势场r处出现的概率密度。

QPSO的设计思想为，首先选择某种不显含时间t的势阱V(r)，然后通过求解式(6)的薛定谔方程得到变量分离形式的波函数Ψ(r)，进而得到粒子在势阱中出现的概率密度函数|Ψ(r)|2，最后通过将势阱中心设置为式(4)定义的最优解，并合理设计势阱参数，可使粒子以大概率逼近式(4)定义的位置。下面以方势阱为例说明QPSO的构造过程。

方势阱的势能分布可表示为:

其中，W为势阱宽度;V0为势阱高度。

粒子在r处出现的概率密度函数为［7］:

其中，a，b，ξ，η为待定常数。

式(8)含有多个束缚态，构造QPSO时只需考虑能量最小的束缚态(基态)，根据量子力学理论，此时ξ＜π，为简便取ξ=1。根据波函数及其导数在r=±W/2处的连续性，式(8)可重写为:

为使当前在r处的粒子下次移动时以较大概率向势阱中心靠近，式(9)需满足如下条件:

由式(9)和式(10)可得势阱宽度W必须满足:

其中，g＞1。

在势阱中的粒子动态行为服从薛定谔方程，在任一确定时刻，其位置是不确定的;而普通PSO中的粒子服从牛顿力学，在任一确定时刻，必须具有确定的位置。这个矛盾可借助波函数的坍缩得以圆满解决。具体可用蒙特卡洛方法。首先在(0，1)内取随机数u，令u=cos2(r/W)，最后解出:

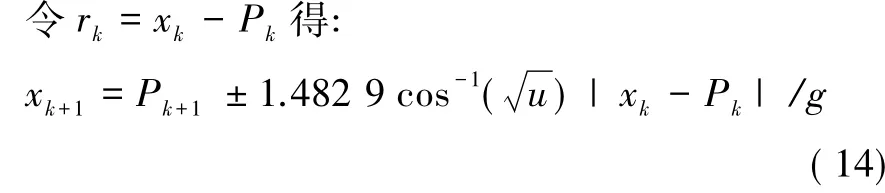
为使QPSO收敛，令

其中，λ＞1。

此时满足式(11)中g＞1的条件。代入式(14)可得:

式(16)即为QPSO的迭代方程。该方程只含一个可调参数λ，从而有利于优化过程的调整。

3 基于QPSO的油水井措施优选

3.1 矿场数据资料

油水井常用措施共12种，每种措施涉及的单价及该措施施工井数的年度上限指标如表1所示。原始数据如表2所示。

3.2 适应度函数设计

(1)目标函数。

其中，ai为日增油;bi为日增液;ci为日增注;di为措施天数;d－i为有效期;pi为单井措施价格。

(2)约束条件。

(3)适应度函数设计。

针对该问题，采取了将约束条件和目标函数融合的设计方法，即当所有约束都满足时适应度函数值最大，否则适应度下降。考虑到约束条件③～⑤为等式约束，因此适应度函数按式(21)设计。

3.3 优化过程设计

(1)参数初始化。

设油井和水井总数为N，每一口井需要优化两个变量，即是否选中(0:否，1:是)和措施天数。因此优化空间为2N维。种群规模取100，限定步数取1 000，变异概率取0.05。

(2)粒子初始化。

为增强粒子的多样性，对每个粒子的前N维随机在［－0.25，0.25］中取值(代表0)，或随机在［0.75，1.25］中取值(代表1);后N维描述该井施工的措施天数，在不超过施工限制天数(有效期)下随机赋值。

(3)变异策略设计。

影响粒子寻优性能的一个障碍就是早熟收敛，即种群粒子趋于一致，从而迫使寻优终止。引入变异策略可有效增强种群多样性，避免早熟收敛。在智能优化算法中，通常的变异策略是针对个体上某一维的，考虑到措施方案优选问题的高维复杂性，采取将变异策略改进为针对个体上所有维，即若满足变异概率，则随机选取一个粒子并将其初始化为新粒子。实验结果表明，这样可有效增强种群多样性。

3.4 优化结果

该问题属于高维空间的多变量、多约束、非线性、强耦合连续优化问题，复杂度较高。采用QPSO按上述策略实施优化，三次典型的优化结果如表3所示。

由表3可知，三次优化的结果比较接近，油水井各种措施方案的施工主要集中在上半年，这与实际采油厂的施工安排是一致的，且能获得更为理想的经济效益。采用QPSO实施措施方案优选的优点在于，不仅可以避免极为繁琐的手工计算，提高工作效率，而且也能获得更为理想的措施优选方案。

4 结束语

文中提出一种用于油水井措施方案优选的量子粒子群优化算法。该算法采用量子力学理论建立搜索机制，具有强大的全局搜索能力。对于油水井措施方案优选问题具有一定潜力。

数值实验证实，该方法操作简单，灵活易用，且有较快的收敛速度。

该预测方法可为油田开发规划的编制和计划安排提供较为合理的依据。

［1］ 赵国忠，孟曙光，姜祥成.聚合物驱含水率的神经网络预测方法［J］.石油学报，2004，25(1):70-73.

［2］ 关晓晶，魏立新，杨建军.基于混合遗传算法的油田注水系统运行方案优化模型［J］.石油学报，2005，26(3):114-117.

［3］ Cai X J，Cui Z H，Zeng J C，et al.Dispersed particle swarm optimization［J］.Information Processing Letters，2008，105(6): 231-235.

［4］ Lin S W，Ying K C，Chen S C，et al.Particle swarm optimization for parameter determination and feature selection of support vector machines［J］.Expert Systems with Applications，2008，35(4):1817-1824.

［5］ 张英杰，邵岁锋，Niyongabo Julius.一种基于云模型的云变异粒子群算法［J］.模式识别与人工智能，2011，24(1):90-96.

［6］ 朱海梅，吴永萍.一种高速收敛粒子群优化算法［J］.控制与决策，2010，25(1):20-24.

［7］ Kennedy J，Eberhart R C.Particle swarms optimization［C］// Proceedings of IEEE international conference on neural networks.USA:IEEE，1995:1942-1948.

［8］ Li L L，Wang L，Liu L H.An effective hybrid PSOSA strategy for optimization and its application to parameter estimation ［J］.Applied Mathematics and Computation，2006，179(1): 135-146.

［9］ 赵新超，刘国莅，刘虎球，等.基于非均匀变异和多阶段扰动的粒子群优化算法［J］.计算机学报，2014，37(9):2058-2070.

［10］钱玉良，张 浩，彭道刚，等.基于EMD调制和粒子群模型的发电机组轴心轨迹提纯［J］.信息与控制，2013，42(2): 243-251.

［11］白国振，荆鹏翔.基于改进粒子群算法的并联机械手运动学参数辨识［J］.信息与控制，2015，44(5):545-551.

［12］方 伟，孙 俊，谢振平，等.量子粒子群优化算法的收敛性分析及控制参数研究［J］.物理学报，2010，59(6):3686-3694.

［13］Said M M，Ahmed A K.Quantum particle swarm optimization for electromagnetic［J］.IEEE Transactions on Antennas and Propagation，2006，54(10):2765-2775.

［14］Clerc M，Kennedy J.The particle swarm:explosion，stability，and convergence in a multi-dimensional complex space［J］. IEEE Transactions on Evolutionary Computation，2002，6(1): 58-73.

Measures Optimization for Oil and Water Well Based on Quantum Particle Swarm Optimization

SUN Hao，LI Pan-chi
(School of Computer and Information Technology，Northeast Petroleum University，Daqing 163318，China)

Measures optimization for oil and water well is one of the important problems in the development of oil field.Currently this issue relies mainly on manual calculation of the technical personnel by their experiences，which has low efficiency and often can not get the best results.To address this issue，a method based on quantum particle swarm optimization is proposed.On the basis of the thorough study of the existing quantum behaved particle swarm optimization model，the dynamic behavior of a particle in a square potential well is investigated with help of the principle of quantum mechanics，and a novel quantum particle swarm optimization is presented.And then，all oil and water wells are taken 0-1 coding according to their construction situation.By comprehensive considering of the objective function and the constraint conditions of all kinds of measures combination，the fitness function is reasonably designed.In the optimization process，the introduction of mutation strategy increases the population diversity.The experimental results show that the optimizations of this method are satisfactory.

oil and water well construction plan;measures optimization;quantum particle swarm optimization;algorithm design

TP183

A

1673-629X(2016)09-0078-05

10.3969/j.issn.1673-629X.2016.09.018

2015-12-13

2016-04-14< class="emphasis_bold">网络出版时间:

时间:2016-08-23

黑龙江省自然科学基金项目(F2015021)

孙 昊(1992-)，男，硕士研究生，研究方向为智能优化算法;李盼池，博士，教授，研究方向为量子智能优化算法。

http://www.cnki.net/kcms/detail/61.1450.TP.20160823.1359.054.html