基于改进型稀疏自动编码器的图像识别

尹　征,唐春晖,张轩雄

(上海理工大学 光电信息与计算机工程学院,上海　200093)

基于改进型稀疏自动编码器的图像识别

尹征,唐春晖,张轩雄

(上海理工大学 光电信息与计算机工程学院,上海200093)

摘要传统的稀疏自动编码器不具备平移不变性,同时对非高斯噪声较为敏感。为增加网络平移不变的特性,借鉴卷积神经网络的相关理论,通过对原始的像素块进行卷积运算以达到上述目的;而为了提高对非高斯噪声的鲁棒性,自动编码器的代价函数由均方误差改为了最大相关熵准则。通过在MNIST和CIFAR-10数据集上进行试验,结果证明,改进后的方法较传统的自动编码器具有更好地识别效果,识别率提高了2%～6%。

关键词深度学习;自动编码器;卷积神经网络;最大相关熵

Image Recognition Based on Improved Sparse Auto-encoder

YIN Zheng,TANG Chunhui,ZHANG Xuanxiong

(School of Optical-Electrical and Computer Engineering,University of Shanghai for

Science and Technology,Shanghai 200093,China)

AbstractThe traditional sparse auto-encoder lacks invariant translation and is sensitive to non-Gauss noise.A method convolving the original pixel block is proposed to increase the network invariance with the mean square error (MSE) replaced by the maximum correntropy criterion (MCC) in cost function to improve the anti-noise ability.The proposed method is evaluated using the MINIST and CIFAR-10 datasets.Experimental results show that the proposed approach improves the recognition rate by 2% in the condition of non-noise and by 6% in the noise condition.

Keywordsdeep learning;auto-encoder;convolutional neural network;maximum correntropy criterion

由于深度学习能够具有模拟人类大脑结构的功能,通过组合底层特征形成更加抽象有效的特征表达来完成对图像的整体描述[1]。深度学习可看成是神经网络发展的产物,传统的多层神经网络在采用深度架构时,因采用BP训练算法,系统容易陷入局部最优。而深度学习有效地克服了这种弊端,已成功应用于图像识别、语音识别、人脸识别等领域。

自动编码器(Auto-Encoder)是典型的深度学习框架之一,由Bourlard在文献[2]中被提出,但主要的应用和发展是在2006年Hinton在文献[3]中提出了一种解决深度信念网(Deep Belief Network,DBN)不易训练问题的方法--贪婪逐层训练算法,该种算法通过无监督学习对网络进行逐层训练,与传统的BP算法训练多层神经网络相比,主要有3大优势:(1)无需大量含有标签的数据集,降低了网络对数据集的要求;(2)加快了神经网络的收敛速度;(3)通过无监督学习,系统在进行微调之前,网络参数已设定在最优参数附近,解决了传统神经网络易陷入局部最优的问题。在文献[4]中将这种算法应用到自动编码器中,解决了多层自动编码器—堆叠自动编码器(Stacked Auto-Encoder,SAE)不易训练的问题。

1基本理论

1.1　自动编码器

传统的自动编码器分为3层,分别为输入层、隐层和输出层。

编码器通过非线性映射函数将输入向量x以一定的方式映射到隐层y,由此y便成为了输入x的另一种表现形式。编码器的原理为

y=fθ(x)=s(Wx+b)

(1)

s(t)=1/(1+exp(-t))

(2)

其中,x∈[0,1]d,y∈[0,1]d,W是d×d′的权重矩阵;b为输入层偏置向量;θ={W,b},s(·)为Sigmoid函数,如式(2)所示。

解码器负责将隐层形成的编码y映射到输出层z,输出层具有和输入层相同的单元数,映射关系如下所示

z=gθ′(y)=s(W′+y+b′)

(3)

其中,z∈[0,1]d,W′是隐层到输出层的权重矩阵;在数值上与W的转置相同;b′为隐层的偏置向量;θ′={W′,b′},将参数合并为θ={θ,θ′}={W,b,b′}。

文中通过训练来调节参数θ,使得输入与输出之间重构误差函数—代价函数最小。传统自动编码器采用的代价函数为MSE

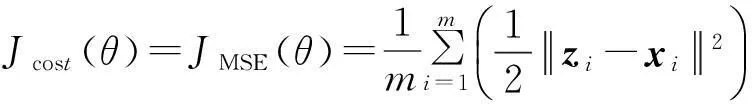
(4)

其中,m为样本的数量;xi为输入向量;zi为输出向量;θ为网络中所有参数的集合。

但为解决自动编码器中过拟合的问题,通常会在代价函数中增加一个权重衰减项,权重衰减项相当于对网络的权重矩阵做了一定的限制,代价函数变为

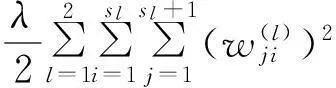
(5)

其中,λ决定了权重衰减项在代价函数中所起的作用;l为网络的层数;sl为l层单元的个数;wji为权重矩阵中角标为j,i的元素值。

1.2　稀疏自动编码器

稀疏自动编码器是自动编码器的一种改进形式。在计算机视觉中,稀疏性约束能够使得编码后的表达更有意义,在独立成分分析(ICA),稀疏编码等算法中已经表现出了良好的性能[5],因此人们在深度学习的优化过程中也加入了稀疏性的限制,主要是通过对每个隐层单元的响应添加约束条件,使隐层单元的大多数神经元处于“抑制”状态,只有少数神经元处于“兴奋”状态。这种约束反映到数学模型中是通过向代价函数中添加稀疏约束项来实现的,公式如下

Jcost(θ)=JMSE(θ)+Jweight(θ)+Jsparse(θ)

(6)

(7)

(8)

其中,ρj为隐层单元神经元的平均激活度;ρ是人为设置的参数,一般比较小,从式(8)可看出,ρj和ρ越接近,代价函数就越小;β决定了稀疏约束项在代价函数中所起的作用。

2改进的稀疏自动编码器

传统的稀疏自动编码器虽然已经具有良好的分类性能,但其不具有空间平移不变的特性。本文通过将卷积神经网络中卷积层的相关理论与稀疏自动编码器相结合,形成卷积稀疏自动编码器;同时为了增加网络的抗躁能力,用MCC取代MSE作为编码器的代价函数。

2.1　卷积稀疏自动编码器

卷积稀疏自动编码器结构如图1所示。

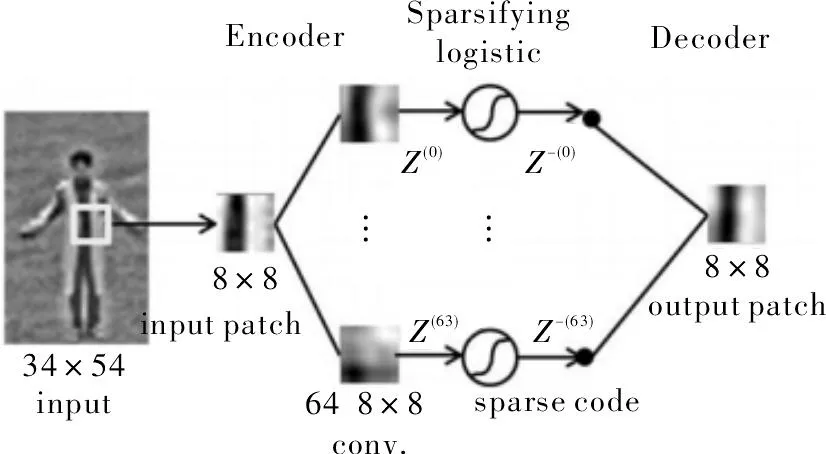
图1　卷积自动编码器结构图

从图像中随机抽取一个8×8的图像块作为输入,之后用相同大小的卷积核分别与此图像块进行卷积,为实现稀疏性,采用卷积核种类数与图像块像素数相等的策略,即64种;64种卷积核对应隐层中的神经元个数为64,每一个神经元所需参数为8×8+1=65个,而64个神经元参数共为4 160个;在解码阶段,输出层的每个神经元与隐层的所有神经元全连接,参数个数为64×64+1=4 097个。对不同的图像块进行编码、解码时,由CNN的权重共享[6]可知,同一种卷积核对应不同的神经元,网络参数值不变。这样当组合输入图像时,虽然隐层的神经元总数增加了,但参数个数并未改变。

此算法采用无重叠滑动窗口策略进行遍历,即步长与窗口大小相同。每个图像块都按照上面的过程进行编、解码,在编码阶段通过加入稀疏性约束,使得隐层响应稀疏。最后,通过合并各个图像块的表示来形成整幅图像的描述,原理如图2所示。

图2　完整图像描述原理示意图

2.2　MCC自动编码器

从文献[7]可得到不同的代价函数对网络的性能起着至关重要的作用。传统自动编码器的代价函数采用MSE,但MSE对于非高斯噪声敏感。针对此问题,本文提出用MCC替换代价函数中的MSE以达到抑制非高斯噪声的目的。

2.2.1相关熵

在文献[8]中,相关熵作为一种局部相似性衡量标准被提出,并已被应用到信号处理领域中,在对抗非高斯噪声上其比MSE具有更好的效果[9]。相关熵是对两个随机变量与相似度的通用计算方法,定义为[10]

Vσ(X,Y)=E[κσ(X-Y)]

(9)

其中,E[·]代表期望;κσ是满足Mercer理论[11]的核函数,本文采用高斯核函数

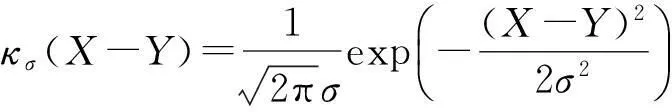
(10)

相关熵利用核函数,将输入空间非线性地映射到高维空间,但与传统的核方法不同,其使每个样本不相关。相关熵是一种局部的相似性度量方法,这点与全局的MSE不同。

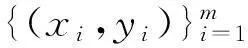
(11)

2.2.2MCC代价函数

在传统的稀疏自动编码器中,网络的代价函数如式(6)所示,本文将用MCC代替MSE,网络的代价函数变为

Jcost(θ)=-JMSE(θ)+Jweight(θ)+Jsparse(θ)

(12)

(13)

其中,m为样本数量;n为每个样本的维数,从式(12)和式(13)可知,要使代价函数最小,则需要相关熵项最大。

3实验结果与分析

为验证本文算法的有效性,选取MINIS和CIFAR-10数据集进行实验。自动编码器只完成了图像的特征提取,本文选用Soft-Max分类器作为网络的输出层来实现分类,并在Matlab-2010软件上进行仿真实验。

3.1　数据集简介

MNIST是一个手写的数字库,其共有60 000张训练图片,10 000张测试图片,每张图片大小为28×28像素,MNIST数据集,图片背景单一,相对而言较易识别。

CIFAR-10是一种小图像的数据集,每幅图像的大小为32×32像素、彩色图像,共有60 000张图像,其中50 000张作为训练图像,10 000张作为测试图像。

在实验之初,首先对CIFAR-10图像数据进行简单的预处理,包括灰度转换及归一化处理。

3.2　实验结果与分析

实验采用3层神经网络结构,并以识别错误率为标准。实验1对MNIST数据集进行实验,分别采用传统的神经网络、稀疏自动编码器、深度信念网和本文提出的标准卷积自动编码器(代价函数为MSE)进行实验。网络的各层单元数为784-784-10,卷积自动编码器采用49种7×7大小的卷积核,步长为7。采用MSE作为编码器的代价函数,是为了与实验3中将对加入非高斯噪声的样本进行分类,届时再采用MCC的卷积自动编码器,这样有利于更好地分析MCC的性能。在实验1中,由于MNIST数据集相对容易识别,文中将迭代次数(包括预训练和微调阶段)设置为20和50,每种网络进行5次实验,取其平均值作为结果,如表1所示。

表1　MNIST的分类结果

从表1可看出,本文所提方法较传统的神经网络(NN),DBN,SpAE在识别率上有了一定的提高。与传统的稀疏自动编码器相比,识别率提高了2%,说明将卷积层的相关理论应用到自动编码器中能够提高网络的识别性能。

实验2采用CIFAR-10数据集进行实验,各层网络单元数为1024-1024-10,迭代次数为50和100;卷积自动编码器采用64种不同的8×8卷积核,步长为8,代价函数为MSE。实验结果,如表2所示。

表2　CIFAR-10的分类结果

从表2可看出,在CIFAR-10数据集上,卷积自动编码器比传统的稀疏自动编码器识别错误率低了将近6%,比DBN网络低了将近5%。

实验3在MNIST数据集中加入非高斯噪声,实验参数与实验1基本相同,但卷积自动编码器的代价函数由MCC代替MSE,结果如表3所示。

表3　加噪声的MNIST数据集分类结果

从表3中可看出,与实验1相比所有模型的错误识别率均有不同程度地提高,但采用MCC代价函数的卷积自动编码器相对于其他模型错误率增加较小;当加大非高斯噪声的强度时,MCC编码器识别变化速率最小,说明MCC作为代价函数对于非高斯噪声具有良好的鲁棒性。

4结束语

本文通过对传统的自动编码器进行改进,将CNN和MCC理论应用到稀疏自动编码器中,实验证明此方法是有效的。虽然深度学习已经得到了广泛地应用,但仍有诸多方面需要研究,例如探索新的深度学习模型等。此外,有效的可并行训练算法也是值得研究的方向之一。

参考文献

[1]BengioY,DelalleauO.Ontheexpressivepowerofdeeparchitectures[C].Berlin,Heidelberg:AlgorithmicLearningTheory,Springer:2011.

[2]BourlardH,KampY.Auto-associationbymultilayerperceptronsandsingularvaluedecomposition[J].BiologicalCybernetics,1988,59(4-5):291-294.

[3]HintonG,OsinderoS,TehYW.Afastlearningalgorithmfordeepbeliefnets[J].NeuralComputation,2006,18(7):1527-1554.

[4]BengioY,LamblinP,PopoviciD,etal.Greedylayer-wisetrainingofdeepnetworks[J].AdvancesinNeuralInformationProcessingSystems,2007(19):153-160.

[5]郑胤,陈权崎,章毓晋.深度学习及其在目标和行为识别中的新进展[J].中国图象图形报,2014,19(2):175-184.

[6]LeCunY,BottouL,BengioY,etal.Gradient-basedlearningappliedtodocumentrecognition[J].ProceedingsoftheIEEE,1998,86(11):2278-2324.

[7]AmaralT,SilvaLM,AlexandreLA,etal.Usingdifferentcostfunctionstotrainstackedauto-encoders[C].12thMexicanInternationalConferenceonArtificialIntelligence(MICAI),IEEE,2013.

[8]LiuW,PokharelPP,PrincipeJC.Correntropy:Alocalizedsimilaritymeasure[C].IJCNN’06,InternationalJointConferenceonNeuralNetworks,IEEE,2006.

[9]HeR,ZhengWS,HuBG,etal.Aregularizedcorrentropyframeworkforrobustpatternrecognition[J].NeuralComputation,2011,23(8):2074-2100.

[10]LiuW,PokharelPP,PríncipeJC.Correntropy:propertiesandapplicationsinnon-gaussiansignalprocessing[J].IEEETransactionsonSignalProcessing,2007,55(11):5286-5298.

[11]VapnikV.Thenatureofstatisticallearningtheory[M].Berlin:SpringerConpration,2000.

作者简介:尹征(1989—),男,硕士研究生。研究方向:计算机视觉等。唐春晖(1971—),男,讲师。研究方向:数字图像处理等。张轩雄(1965—),男,教授。研究方向:微电子机械系统等。

收稿日期:2015- 05- 05

中图分类号TN762;TP242

文献标识码A

文章编号1007-7820(2016)01-124-04

doi:10.16180/j.cnki.issn1007-7820.2016.01.034