发电机仿真分析及优化设计

张青雷,高孟雪

(1.上海理工大学 机械工程学院,上海　200093;2.上海电气集团股份有限公司 中央研究院,上海　200073)

发电机仿真分析及优化设计

张青雷1,2,高孟雪1

(1.上海理工大学 机械工程学院,上海200093;2.上海电气集团股份有限公司 中央研究院,上海200073)

摘要为建立更加精确的汽轮发电机定子端部的有限元模型,以汽轮发电机定子绕组的汽端为研究对象,用有限元分析法进行模态分析。结合模态试验测得的数据,分析误差来源,选择有限元模型修正参数。基于Ansys Workbench仿真软件的优化模块对修正参数进行灵敏度分析,保留灵敏度高的参数,并对保留的参数进行优化分析。研究结果表明,经修正后的有限元模型能准确地反映该结构真实的动力特性,且仿真模态与试验模态之间的误差减小在5%以内。

关键词汽轮发电机;模态分析;灵敏度分析;模型修正;优化设计

Finite Element Analysis and Optimization of Generator

ZHANG Qinglei1,2,GAO Mengxue1

(1.School of Mechanical Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China;

2.Central Academy,Shanghai Electric Group Co.,Ltd.,Shanghai 200070,China)

AbstractThe steam generator side of the stator end winding of tur-generator is studied with a modal analysis by finite element method to establish a more accurate finite element model of stator end winding of tur-generator.The modal experiment data are analyzed to show the error sources,based on which the modification parameters of the finite element model are selected.After the sensitivity analysis of modal parameters based on Ansys Workbench,the high sensitivity parameters retained are updated.The results demonstrate that the model updated by simulation calculation can reflect the real dynamic characteristics of the structure with the difference between simulation and experimental less than 5%.

Keywordsturbo generator;modal analysis;sensitivity analysis;model updating;optimization design

汽轮发电机定子绕组端部由于电磁力作用而引起的振动会造成绝缘层损坏和噪声。为避免这种情况,在设计过程中采用有限元仿真与试验测试相结合的方法,对汽轮发电机定子绕组端部的固有振动特性进行预测是必要的[1]。在进行发电机定子绕组端部振动特性分析时,运用有限元法得到一个近似地描述端部结构动力特性的计算模型,为使设计对象的动态参数满足设计需要,对有限元模型的参数修正是必要的。文献[2~4]对模型修正的理论方法进行了研究,文献[5~6]分别对斜拉桥和机床进行优化分析。本文以发电机的汽端为研究对象,对结构进行模态计算,基于Ansys Workbench软件的灵敏度分析,对仿真模型进行优化设计,提高了其动力特性,为发电机的优化设计提供参考。

1模态分析理论基础

现以单自由度系统为例说明机械结构的振动特性。图1所示为单自由度振动系统的物理参数模型,其振动微分方程为[7]

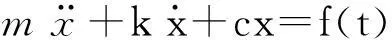
(1)

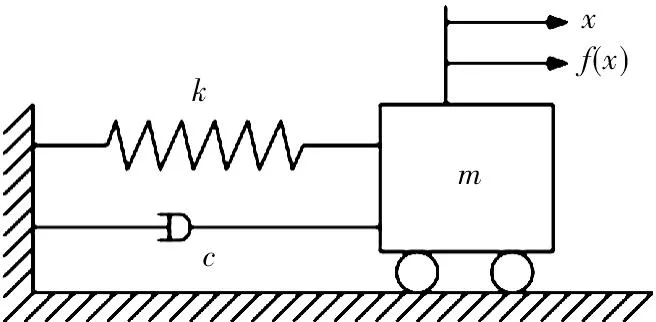
图1　单自由度振动系统

当单自由度系统为自由振动时,其微分方程为

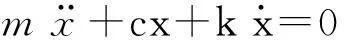
(2)

或者写成正则形式为

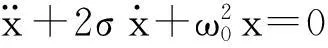
(3)

则式(3)可写成

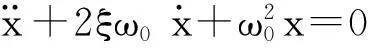
(4)

方程(4)特解为:x=φeλt,λ为方程的特征值,因此

(mλ2+cλ+k)φ=0

(5)

若系统有非零解,则

mλ2+cλ+k=0

(6)

因此可得到λ的解为λ1,2=-σ±jωd,λ的实部代表系统的衰减指数;λ的虚部代表系统的固有频率。

2仿真分析及试验分析

2.1　仿真模态分析

本文用UG8.0对发电机定子绕组汽端进行三维建模,定子绕组端部结构复杂,遵循刚度和质量等效原则,通过去除一些细小结构,如小孔、槽等,得到简化后的有限元模型如图2所示,简化后再进行有限元分析。采用四面体实体单元进行网格划分,有限元网格划分的单元数为116,792,节点数为577,129。得到汽端发电机定子端部有限元模型如图3所示。

图2　汽端简化三维模型

图3　汽端有限元模型

经有限元分析,可得到汽轮发电机定子端部绕组汽端的振动模态及频率,其振型如图4所示。汽端一阶椭圆频率值为97.074 Hz,二阶椭圆频率值121.1 Hz。

图4　汽端椭圆模态

2.2　试验分析

试验采用锤击法,试验前在测试系统软件中建立相应的测点模型,依次对测点模型中的各个测点进行测量,如图5所示,其测试结果如图6所示。

图5　测点模型示意图

汽端有限元计算结果与试验结果对比分析如表1所示。

表1　仿真结果与试验结果误差

为能够准确地反映实际模型,减小仿真结果与试验结果之间的误差,现对此有限元模型进行修正。

3有限元模型修正

3.1　修正参数的选择

在模型修正过程中,一个至关重要的步骤就是模型修正参数的选择[8],这也是模型修正成功与否的关键所在。

由于定子绕组端部各部件的材料属性较复杂,且在计算过程中根据图纸上给出的参数范围选取材料参数,因此材料属性参数具有明显的不确定性。对有限元模型的8个材料属性参数进行筛选,如表2所示。为使修正模型准确且有意义,需对这8个材料属性变量值设定上下限,即计算中所容许的变化范围。由于线棒及锥环的结构复杂,且含有绝缘层等非线性材料,因此允许其弹性模量在±30%内变化,考虑到整体连接刚度的变化,允许垫块及压板的弹性模量同样有±30%的变化范围,由于线棒、锥环、压板、垫块在建模时均作了简化,允许其密度有±20%的变化[9]。

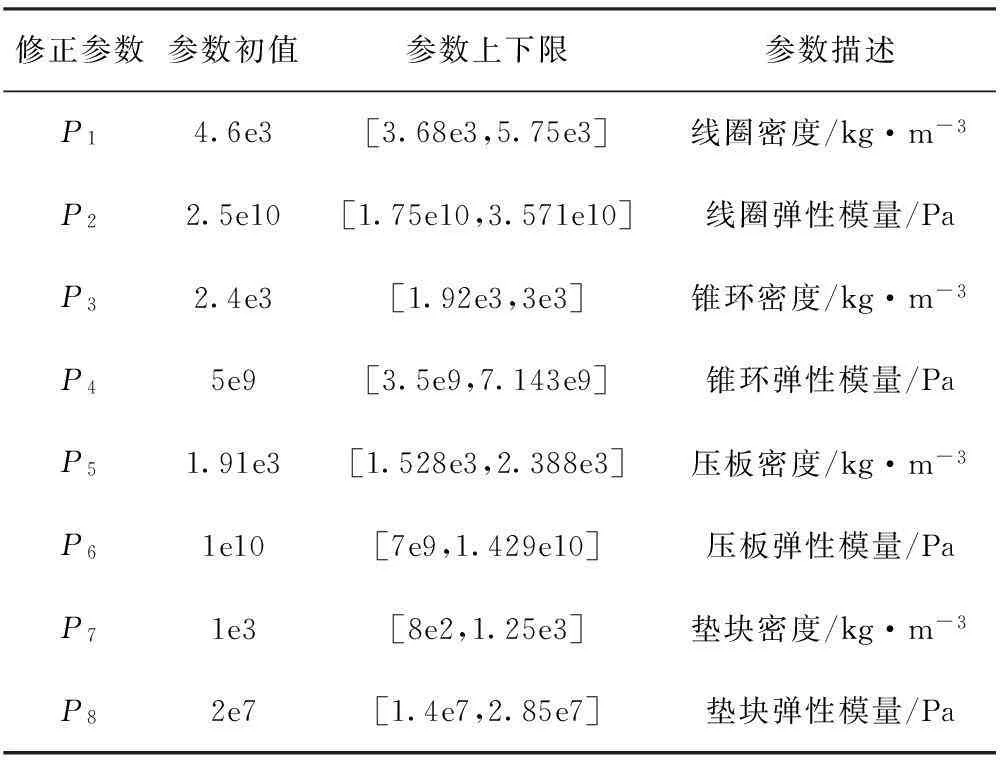
表2　待修正参数及其上下限

3.2　参数灵敏度分析

参数型修正法作为模型修正最行之有效的方法之一,是指对结构的截面形状,材料属性、几何尺寸等参数进行修正的方法,包括模态法和频响函数法,基于模态参数灵敏度的修正方法根据截取的泰勒展开式,使迭代过程所取的修正参数最优。参数型修正法是指对测量数据中所包含的参数进行修正,其数量不可能无限多,因此对整个系统的灵敏度最高的参数进行修正,这就需要对系统进行灵敏度分析。在结构动态特性分析中,某特征向量f对某物理量p的泰勒展开式为

(11)

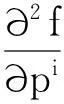
目标参数为定子绕组汽端第一阶和第二阶椭圆模态所对应的频率值。基于AnsysWorkbench的优化模块对修正参数进行灵敏度分析,得到目标参数关于修正参数的灵敏度,如图7所示。

图7　设计参数对目标参数的灵敏度

如图7所示,修正参数P1、P2、P3、P4、P6、P8对应的线圈的密度、线圈的弹性模量、锥环的密度、锥环的弹性模量、压板的弹性模量和垫块的弹性模量对目标参数的反应灵敏度较大,而参数P5、P7即压板密度和垫块密度反应灵敏度较小,说明对目标参数影响较小,进行剔除。接下来对灵敏度高的6个参数进行修正。

3.3　有限元模型修正结果

基于仿真软件的优化模块,在设定的上下限内修正6个灵敏度高的参数,共81个设计点,其中部分设计点如表4所示。对这81个设计点进行计算,可得如图8所示的计算结果,横坐标为设计点,纵坐标左边为第一阶椭圆模态对应的频率,右边为第二阶椭圆模态对应的频率。

图8　模型修正结果

由图8可看出,线上的每个点所对应的第一阶和第二阶椭圆模态的频率值在一定的变化范围内,其中设计点78所对应的一阶频率值为100.75 Hz、二阶频率值为129.59 Hz接近试验结果,如图8和表4所示。此时6个灵敏度高的设计参数的修正值如表3所示。

表3　设计参数的修正值

表4　部分设计点对应的参数值

有限元模型修正后的结果如表5所示,经过模型修正,试验模态与仿真模态对应频率的误差减小在5%以内,该误差值在可接受的范围内。

表5　仿真结果、试验结果与修正后结果误差分析

4结束语

灵敏度分析结果可知压板和垫块的密度对端部模态影响较小,可忽略不计。对灵敏度高的6个参数进行修正,其结果与试验值接近,可反映真实的动力特性,提高了有限元模型的精度,对汽轮发电机定子绕组端部的设计及优化提供一定数据支持。

参考文献

[1]Schlegl B,Schönleitner F,Marn A,et al.Analytical Determination of the orthotropic material behavior of stator bars in the range of the end windings[C].Changsha:Power Electronics,Machines and Drives (PEMD 2012),2012.

[2]Linderholt A,Abrahamsson T.Optimizing the informativeness of Test data used for computational modal updating[J].Mechanical Systems and Signal Processing,2005(19):736-750.

[3]Kerschen G,Worden K,Vakakis A F,et al.Past,present and future of nonlinear system identification in structural dynamics[J].Mechanical Systems and Signal Processing,2006(20):505-592.

[4]Li Huajun,Wang Junrong,Hu Saulon.Model updating based on incomplete modal data[J].Science China Technological Sciences,2011(7):1737-1747.

[5]周林仁,欧进萍.斜拉桥结构模型修正的子结构方法[J].振动与冲击,2014,33(19):52-58.

[6]曹宏瑞,何正嘉.机床-主轴耦合系统动力学建模与模型修正[J].机械工程学报,2012,48(3):88-94.

[7]曹树谦,张文德,萧龙翔.振动结构模态分析—理论实验与应用[M].天津:天津大学出版社,2001.

[8]姜东,丁继锋,费庆国.一种有限元模型修正中的参数选择方法[J].固体力学学报,2011,32(10):88-92.

[9]李坤.汽轮发电机定子的结构强度与振动分析[D].杭州:浙江大学,2010.

作者简介:张青雷(1973—),男,博士,高级工程师。研究方向:数字化设计及制造。高孟雪(1990—),女,硕士研究生。研究方向:数字化设计及制造。

基金项目:上海市2013年度服务业发展引导基金资助项目(cn2013000016)

收稿日期:2015- 05- 05

中图分类号TM311;TH164

文献标识码A

文章编号1007-7820(2016)01-056-04

doi:10.16180/j.cnki.issn1007-7820.2016.01.015