大型风电法兰用Q345E钢动态再结晶行为研究
2016-02-29张秀芝杨仁杰刘建生
张秀芝 杨仁杰 李 佳 刘建生
(太原科技大学材料科学与工程学院,山西030024)
大型风电法兰用Q345E钢动态再结晶行为研究
张秀芝杨仁杰李佳刘建生
(太原科技大学材料科学与工程学院,山西030024)
摘要:在不同温度、不同应变速率条件下进行了热压缩试验,并对各种条件下的应力-应变曲线进行了分析,研究表明当温度高于1 000℃时材料均发生了不同程度的再结晶。通过对不同变形条件下材料的晶粒尺寸分析,建立了Q345E钢动态再结晶分数模型、晶粒尺寸模型以及力学模型,为热加工工艺的制定提供了理论基础。
关键词:Q345E;风电法兰;动态再结晶

Q345E钢具有较高的强度,良好的冷变形能力,较好的塑性与韧性,能抵抗过载能力,广泛应用于大型风电法兰的生产及其它行业中。刘海英和王从道等人对Q345E钢的热塑性方面进行了研究[1,2]。本课题组前期提出了Q345E钢的本构方程,并得出了材料的动态再结晶图[3]。但动态再结晶分数、动态再结晶后晶粒尺寸与工艺参数的关系尚不明确,因此在前期工作的基础上系统研究了Q345E钢热变形过程中的力学模型、再结晶分数模型、晶粒尺寸模型,为后期风电法兰辗扩过程模拟提供理论依据,并为制定风电法兰热加工工艺提供理论基础。
1实验材料及方法
所用材料为Q345E钢,其主要化学成分见表1。试样尺寸为∅8 mm×12 mm的圆柱体。热变形试验采用热压缩法,实验设备为Gleeble-1500D热模拟试验机。试验温度为900℃、950℃、1 000℃、1 050℃、1 100℃、1 150℃、1 200℃。应变速率为0.005 s-1、0.05 s-1、0.5 s-1。形变量为50%(真应变为0.7)。热压缩试验完成后将试样沿轴向切开,经抛光、腐蚀后观察组织,并在ZEISS Imager.A1m金相显微镜上测定晶粒的平均尺寸。

表 1 试样化学成分(质量分数,%)
2实验结果及分析
2.1不同形变参数下的应力-应变曲线
材料在不同温度、不同应变速率下压缩变形的真应力-真应变曲线如图1所示。从图1可以看出,温度、应变速率对材料高温变形行为有明显影响。温度高于1 000℃时,试样都发生了明显的动态再结晶。950℃与1 000℃条件下,当应变速率较低时发生再结晶,但在900℃时没有再结晶发生。

图 1 不同温度、不同应变速率下的应力-应变曲线
2.2动态再结晶峰值应变及稳态应变模型的建立
金属材料发生动态再结晶,峰值应变和稳态应变[4、5]分别可采用以下公式表示:
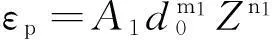
(1)
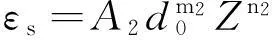
(2)
上式中峰值应变和稳态应变通常采用加工硬化率与应变曲线确定。加工硬化率与应变的曲线[6、7]关系如图2所示。
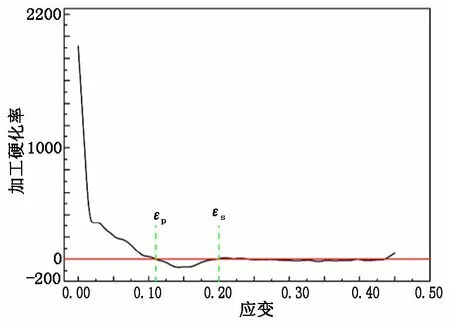
图 2 加工硬化率-应变曲线
分别对式(1)与式(2)取自然对数,得到:

(3)

(4)
将式(3)、式(4)对lnZ微分,利用线性拟合可获得lnεp-lnZ的关系曲线和lnεs-lnZ的关系曲线,如图3示。通过线性拟合,可求得:n1=0.182,n2=0.202,A1=2.501×10-4,A2=2.508×10-4。

(a) lnεp与lnZ的关系曲线

(b) lnεs与lnZ的关系曲线
同理,将式(3)、式(4)对lnd0微分,利用线性拟合可求得lnεp-lnd0的关系曲线和lnεs-lnd0的关系曲线,如图4所示。求得m1、m2分别为0.240与0.110。因此峰值应变、稳态应变模型分别为:

(5)

(6)
2.3动态再结晶百分数模型的建立
动态再结晶百分数模型采用Avrami方程[8、9]的普遍形式:

(7)
整理式(7),得到:
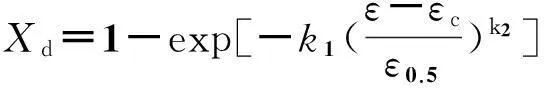
(8)

(a) lnεp与lnd0的关系曲线

(b) lnεs与lnd0的关系曲线
式中,k1、k2为材料常数,εc为材料发生动态再结晶的临界应变;ε0.5为材料变形过程中发生50%再结晶时的变形量,其表达式为:

(9)
式中,α1、α2、α3为材料常数,Qdyn为动态再结晶激活能。
由于金相测量存在人为误差,因此本文采用式(10)[10]确定动态再结晶百分数,即当εcεεs时:

(10)


图 5 热塑变形真应力-真应变曲线示意图
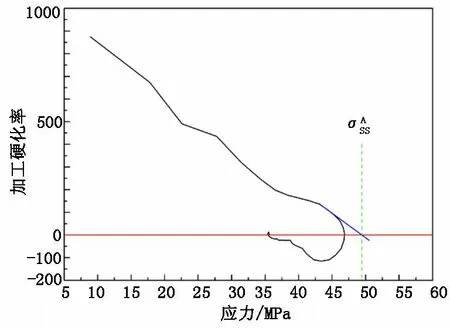
图6 加工硬化率-应力曲线


(11)
将式(8)变形,得到:

(12)

根据文献[11、12]取α=0.83,依据上述得到的各材料参数,从而得出动态结晶百分数模型:

(13)
2.4动态再结晶晶粒尺寸模型的建立

图 7 lnε0.5-lnd0的关系曲线

图 8 lnε0.5-10 000/T的关系曲线

的关系曲线

图 10 ln[-ln(1-Xd)]与
动态再结晶晶粒尺寸主要取决于变形速率,原始奥氏体晶粒尺寸和变形量对其影响很小,可以忽略。因此动态再结晶晶粒尺寸采用Sellars模型[13]表示为:

(14)
式中,A和n是与金属材料自身相关的的常数。
对式(14)两边取自然对数,得到:

(15)
测量不同变形条件下金相的晶粒尺寸,将其代入式(15),并进行线性回归处理,如图11所示。得到:A为 1.61×104,n为 -0.156 7。则动态再结晶晶粒尺寸模型为:

图 11 lndDrex与lnZ的关系曲线
(16)
将参数表达式Z代入式(16),得到完整的动态再结晶晶粒尺寸模型:

(17)
3结论
通过分析、回归得到材料发生动态再结晶的峰值应变、稳态应变模型、动态再结晶百分数模型和动态再结晶晶粒尺寸模型。
参考文献
[1]刘海英,骆春民,张龙.Q345E 钢奥氏体动态再结晶行为研究及数学模型的建立[J].天津冶金,2012(5):14-18.
[2]王从道.Q345E 特厚板动态再结晶行为的研究[J].南钢科技与管理,2012(2):22-25.
[3]李佳,张秀芝,刘建生. 低合金钢Q345E高温热变形行为及动态再结晶图[J].锻压技术,2013(4):148-151.
[4]John J.Jonas,Xavier Quelennec,Lan Jiang,Etienne Martin. The Avrami kinetics of dynamic recrystallization[J]. Acta materialia,2009,57(9):2748-2756.
[5]Schindler I, Hadasik E.A new modle describing the hot stress-strain curves of HSLA steel at high deformation[J]. Materials Processing Technology,2000,106:131-135.
[6]Poliak E I, Jonas J J. Initiation of Dynamic Recrystallization in Constant Strain Rate Hot Deformation. ISIJ Internationa,2003, 43 (5) :684.
[7]吴瑞恒,朱洪涛,张鸿冰.0.95-18W-4Cr-1V 高速钢动态再结晶的数学模型.上海交通大学学报,2001,35(3):339-342.
[8]Hodgson P D,Gibbs R K. A mathematical model to predict the mechanical properties of hot rolled C-Mn and microalloyed steels[J ]. ISIJ International,1992,32(12) : 1329-1338.
[9]Manohar P A,Kyuhwan LIM,Rollett A D,et al. Computational exploration of microstructural evolution in a medium C-Mn steel and applications to rod mill[J].ISIJ International,2003,43(9): 1421-1430.
[10]Wahabi M El,Cabrera J M,Prado J M. Hot working of two AISI 304 steels: a comparative study[J]. Mater Sci Eng A,2003,343: 116-125.
[11]Sellers C M. Computer modeling of hot2working processes[J].Materials Science and Technology , 1985 ,1 (4): 325-332.
[12]Sellers C M. Modeling microstructural development during hot rolling[J]. Materials Science and Technology , 1990 ,6 (11): 1072-1081.
[13]Bontcheva N, Petzov G. Microstructure evolution during metal forming processes[J]. Computational Materials Science, 2003,28:563-573.
编辑杜青泉

Research on Dynamic Recrystallization Behavior of
Q345E Steel for Heavy Wind Power Flange
Zhang Xiuzhi, Yang Renjie, Li Jia, Liu Jiansheng
Abstract:The hot compression test has been performed under various conditions of different temperature and different strain rate. Meanwhile, the stress-strain curves under various conditions have been analyzed. It turned out that when the temperature was higher than 1000℃, the materials all occurred recrystallization with different degree. By analyzing the grain size of materials under different deformation condition, the fraction model, the grain size model and the mechanical model of dynamic recrystallization for Q345 steel have been built up, so as to provide the theoretical basis for preparing the hot working processes.
Key words:Q345E; wind power flange; dynamic recrystallization
基金项目:太原市科技资助项目(120224)。
收稿日期:2015—05—12
中图分类号:TG142.15
文献标志码:B
