P-BRW体系整体结构模型抗震性能分析

周学军，王振，徐源，张慧武，杨融谦，张哲

（1.山东建筑大学土木工程学院，山东济南250101；2.格里菲斯大学工程学院，黄金海岸4222，澳大利亚；3.山东大学土建与水利学院，山东济南250061；4.墨尔本皇家理工大学工程学院，墨尔本3001，澳大利亚）

P-BRW体系整体结构模型抗震性能分析

周学军1，王振1，徐源2，张慧武1，杨融谦3，张哲4

（1.山东建筑大学土木工程学院，山东济南250101；2.格里菲斯大学工程学院，黄金海岸4222，澳大利亚；3.山东大学土建与水利学院，山东济南250061；4.墨尔本皇家理工大学工程学院，墨尔本3001，澳大利亚）

柱贯通型梁端铰接钢框架屈曲约束钢板剪力墙（P-BRW）体系是一种新型抗震结构体系，其受力明确，构造简单，更适合工业化建造的要求。采用有限元分析软件对一幢15层的高层建筑整体结构模型进行了不同地震设防烈度罕遇地震作用下的抗震性能研究，分析其自振特性、楼层位移、层间位移角、塑性出铰机制等性能指标。结果表明：P-BRW体系整体结构可以最大程度的发挥屈曲约束钢板剪力墙的耗能能力；在8度（0.2g）及以下设防烈度罕遇地震作用下，铰接钢框架的梁柱均处于弹性阶段，屈曲约束钢板剪力墙体系屈服而不屈曲，满足“小震不坏，中震可修，大震不倒”的设计原则；但在8度（0.3g）设防烈度罕遇地震作用下，底层柱端会形成塑性铰，不满足抗震设防要求。

P-BRW体系；整体结构模型；罕遇地震；抗震性能；有限元分析

0 引言

目前国家正在大力推广装配式建筑［1-3］，各地均出台了相应的激励政策，但由于多年设计思维的惯性，推广应用的效果并不明显［4-5］。柱贯通型梁端铰接钢框架—屈曲约束钢板剪力墙P-BRW体系是一种适用于多层或小高层建筑的装配式钢结构体系，在该结构体系中，铰接钢框架只承担竖向荷载，而全部的侧向荷载由屈曲约束钢板剪力墙体系承担，其传力机制明确，节点构造简单，更适合工业化建造［6］。对于装配式钢结构建筑而言，主体结构装配的关键在于连接节点的装配。在柱贯通型梁端铰接钢框架中，梁与柱的连接可采用端板螺栓连接、腹板耳板螺栓连接、顶底角钢螺栓连接等多种形式。屈曲约束钢板剪力墙由内嵌钢板和两侧的预制混凝土盖板组成，其中内嵌钢板两侧采用预制钢筋混凝土盖板作为面外约束构件，并在混凝土盖板上预留螺栓孔，通过连接螺栓使两侧盖板与内嵌钢板紧密接触，内嵌钢板与四周框架梁柱的连接由连接板过渡，采用高强螺栓连接［7-8］。由于P-BRW体系中的铰接框架几乎不参与抗侧，为了加强结构体系的整体抗侧性能，屈曲约束钢板剪力墙的布置应尽量均匀对称，与屈曲约束钢板剪力墙相连的梁柱连接为刚接（现场螺栓连接或在工厂预加工），其余的梁柱连接均为铰接，其结构设计应满足：在小震作用下，铰接框架体系和屈曲约束钢板剪力墙体系均保持弹性；中大震作用下，铰接框架体系仍保持弹性，屈曲约束钢板剪力墙屈服而不屈曲，使结构满足“大震不倒”的原则。为了探讨这种新型结构体系整体结构抗震性能，采用有限元软件对“横向五跨、纵向三跨”及地上15层的P-BRW体系整体结构模型进行了自振特性和罕遇地震下的动力弹塑性时程分析，旨在分析该结构体系在合理截面及相应高度下的适用抗震设防烈度。

1 P-BRW体系整体结构模型及结构荷载

柱贯通型梁端铰接钢框架屈曲约束钢板剪力墙（P-BRW）体系整体结构分析模型柱网尺寸为12.6 m×21 m，横向五跨，纵向三跨，每跨均为4.2 m，地上15层，层高均为2.8 m，剪力墙沿高度方向连续布置，整体模型平面布置如图1所示（图中虚线部分为屈曲约束钢板剪力墙）。

按照GB 5009—2012《建筑结构荷载规范》［9］和建筑物主要构造做法的要求，结构所受主要荷载标准值有：楼面恒荷载为3.25 kN/m2，屋面恒荷载为3.5 kN/m2，外墙梁上墙体线荷载为6.02 kN/m，内墙梁上墙体线荷载为3.78 kN/m和屋面女儿墙线荷载为2.0 kN/m。楼面活荷载为2.0 kN/m2，屋面活荷载为2.0 kN/m2（上人屋面）。设计整体结构模型时，梁柱均为Q345级钢材，混凝土均为C30。根据正常使用状态的荷载工况，拟定的构件截面尺寸见表1。

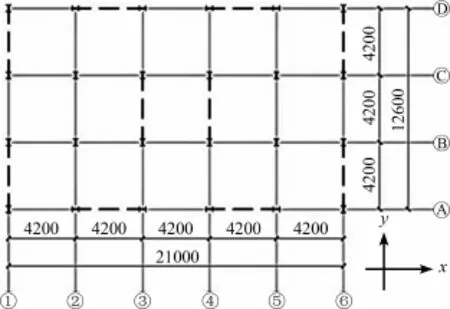
图1 整体模型平面图/mm

2 P-BRW体系整体结构有限元模型的建立

2.1 屈曲约束钢板剪力墙有限元简化模型选择

基于普通薄钢板剪力墙屈曲后产生的拉力带效应，钢板剪力墙的有限元的简化模型主要有等效拉杆模型、相交斜拉杆模型、混合杆系模型等［10-11］。等效拉杆模型［12］将内嵌钢板划分为若干板条，将板条简化成一系列与周边框架铰接的倾角相同的只拉杆，忽略钢板的承压能力，过低估计了钢板墙的耗能能力［13］。相交斜拉杆模型是在等效拉杆模型的基础上反向增加同样的斜拉杆，主要用来研究钢板墙的滞回性能［14］。李然考虑到屈曲约束钢板剪力墙部分钢板保持平面内受力的特点，提出了混合杆系模型，即混合“n-m”模型［15］。其中，n为拉压杆的数量，拉压杆代表了前期钢板剪力墙以平面内受剪为主的承载方式；m为只拉杆的数量，只拉杆代表了后期钢板剪力墙发生屈曲而形成的拉力带作用。经研究发现，混合“4-6”模型可以很好地模拟屈曲约束钢板剪力墙的受力性能，因此，屈曲约束钢板剪力墙有限元简化模型采用混合“4-6”简化模型，只拉杆和拉压杆均采用Frame单元，屈曲约束钢板剪力墙简化模型的设计参数见表2。

表2 混合“4-6”简化模型参数

2.2 材料属性和本构关系

钢材的本构关系采用双线性随动强化模型，强化段切线模量取Est=0.01Es（Es为钢材弹性阶段弹性模量）。在屈曲约束钢板剪力墙“混合杆系”简化模型中，为保证材料屈服准则仍满足Mises屈服准则，将拉压杆的屈服强度取钢材的剪切屈服强度f v

［16］，只拉杆的屈服强度取钢材的拉伸屈服强度fy，拉压杆与只拉杆的本构关系如图2所示。

图2 杆件本构关系图

2.3 框架梁柱单元类型的确定

采用SAP2000有限元分析软件对嵌固端以上结构进行动力弹塑性时程分析，柱脚为刚接。在有限元分析中，与屈曲约束钢板剪力墙连接的框架梁柱节点为理想刚节点，梁端铰接框架梁柱节点为理想铰节点，框架梁、柱均采用Frame单元，楼板采用Shell单元，按弹性楼板考虑。

2.4 塑性铰的设定

为了研究问题的方便，文章在拉压杆和只拉杆的中间位置设置一个P铰（轴力铰），用来模拟钢板剪力墙的拉压屈服；在与屈曲约束钢板剪力墙相连接的梁柱刚接框架中，柱两端设置轴力和弯矩相互作用的P-M2-M3耦合铰，梁两端设置M铰（弯矩铰）；在梁端铰接框架中，柱两端仍设置轴力和弯矩相互作用的P-M2-M3耦合铰，但因梁端铰接，故在梁上M铰布置在跨中位置。

2.5 地震波的选取与非线性设置

选取场地类型为Ⅱ类场地，地震分组为第二组，按照GB 50011—2010《建筑抗震设计规范》［17］中的选波原则，选择EICentro波和Taft波及一条人工波。有限元分析时考虑几何非线性参数和材料非线性参数，几何非线性参数是指P—Δ效应，材料非线性参数指的是框架单元内的拉/压极限设置、框架单元内的塑性铰设置等。

3 P-BRW体系整体结构模型受力分析

3.1 结构的自振特性分析

在分析自振特性时考虑高阶振型对结构的影响，对模型采用Ritz向量法进行自振特性分析。PBRW体系整体结构分析模型的自振特性分析结果的前6阶振型图如图3所示，其自振特性见表3。

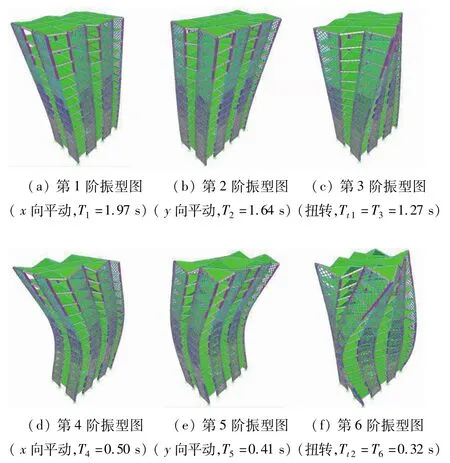
图3 整体分析模型的前6阶振型图

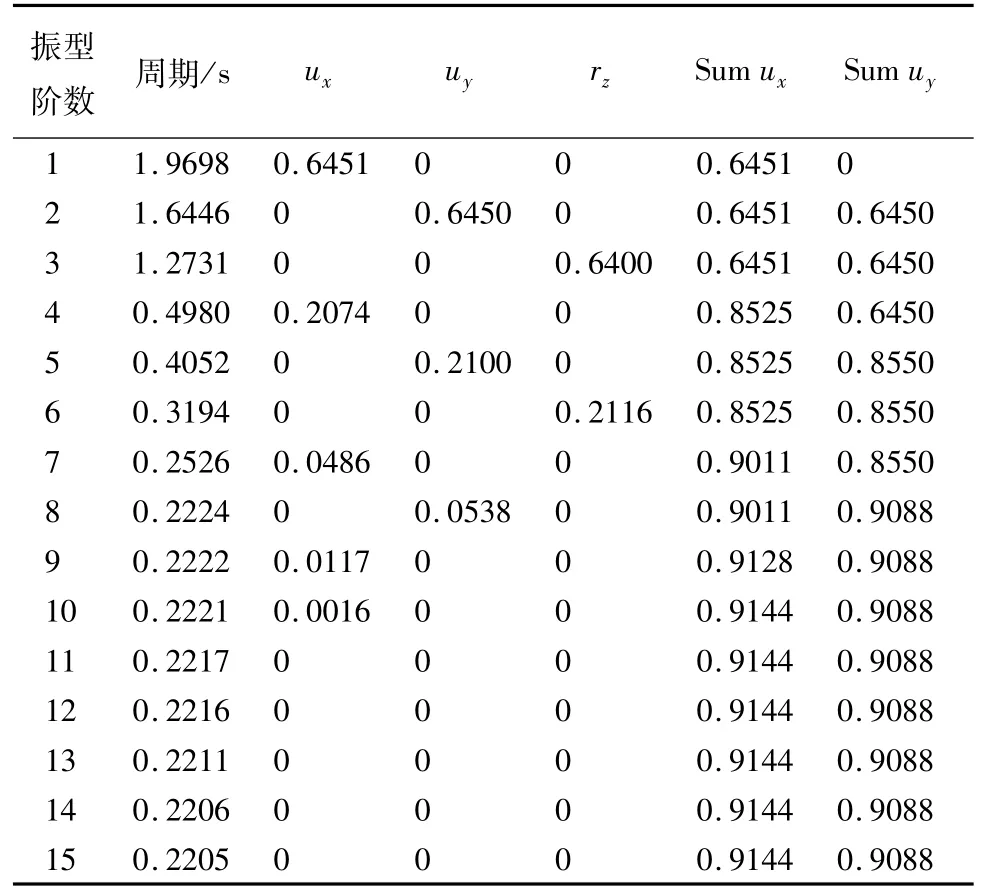
表3 结构自振特性信息表

由表3可知，结构的第1振型为沿x方向的水平振动，在整体模型平面图中，x方向布置的剪力墙较少，故结构沿x方向的抗侧刚度较小，x轴为结构的弱轴。第2振型为沿y方向的水平振动，第3振型为扭转。结构第1振型周期为1.97 s，符合GB 50009—2012《建筑结构荷载规范》建议的经验公式T=0.1 n～0.15 n的要求，其中n为楼层数［9］。结构以扭转为主的第一自振周期Tt1与以平动为主的第一自振周期T1之比为Tt1/T1=

1.273111 /1.969896=0.6463，两者相差较大，说明整体结构模型的扭转效应较小，具有良好的抗扭转能力，结构平面布置合理。此外，当取前15阶振型参与计算时，Sum ux=91.46%，Sum uy=90.89%，满足GB50011—2010《建筑抗震设计规范》中累计水平质量参与系数大于90%的要求［17］。

3.2 动力弹塑性时程分析

对P-BRW体系整体结构模型分别在7度（0.1g）、7度（0.15g）、8度（0.2g）和8度（0.3g）抗震设防烈度下进行罕遇地震时程分析，得到了整体结构模型的楼层位移、层间位移角和塑性铰出铰机制等性能指标，其中g为重力加速度。

3.2.1 楼层位移和层间位移角分析

由于低烈度下结构层位移反应均小于8度（0.3g）设防烈度下的的结构层位移反应，且表现出大致相同的趋势，所以文章不再讨论低烈度下的结构层位移反应。表5和图4分别给出了抗震设防烈度为8度（0.3g）时，P-BRW体系结构整体分析模型在三种地震波作用下结构沿弱轴（x轴）方向顶点位移达到最大值时刻的各楼层位移值和楼层位移曲线。

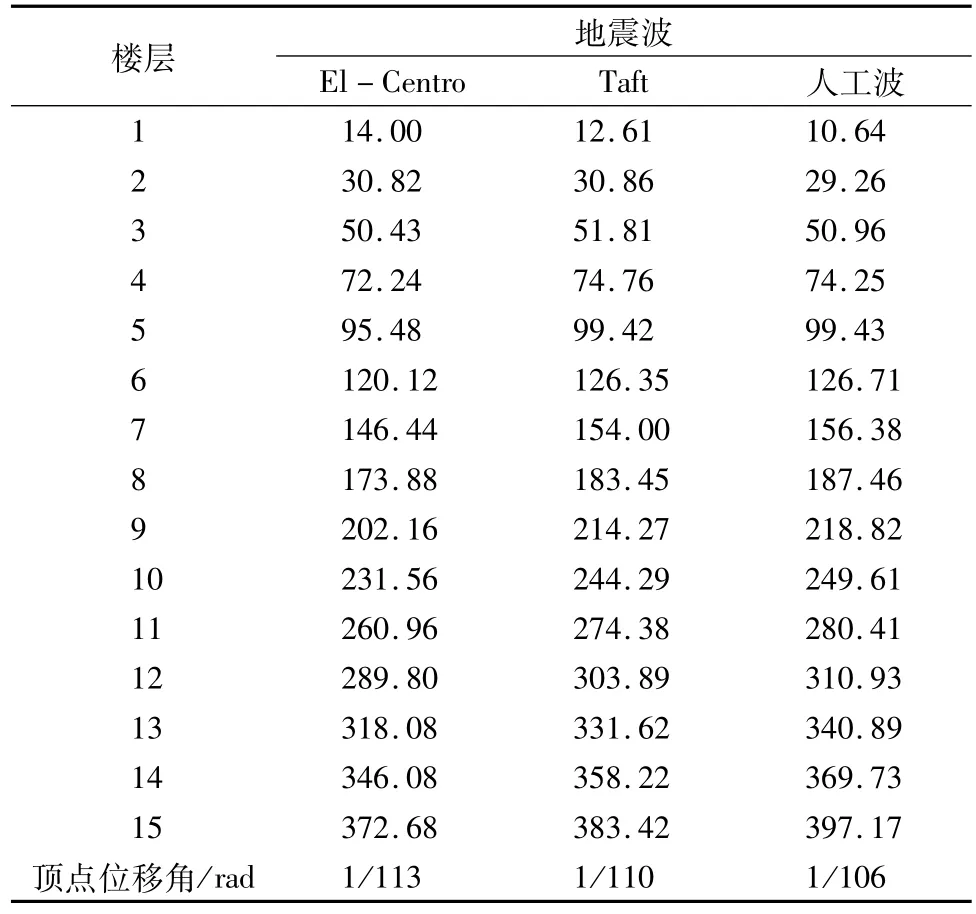
表5 结构顶点沿x方向的位移达到最大值时的各楼层位移值/mm

图4 结构顶点沿x方向的位移达到最大值时的各楼层位移曲线图

根据表5和图4可知，P-BRW体系整体分析模型的顶层平均位移为384.43 mm，其顶点平均位移角为1/109；人工波作用下P-BRW体系整体分析模型的顶层位移最大，为397.17 mm，其顶层位移角为1/106，二者均没有超过JGJ 99—2015《高层民用建筑钢结构技术规程》［18］的限值要求。

抗震设防烈度为8度（0.3g）时，P-BRW体系整体结构分析模型在三种地震波作用下结构沿弱轴（x轴）方向的层间位移角如图5所示。

根据图5可知，在三种地震波作用下，楼层的层间位移角最大值均没有超过GB 50011—2010《建筑抗震设计规范》［17］限值1/50的要求，层间位移角最大值基本出现在结构的中上部，整体侧移表现出典型的弯曲变形特征，层间位移角在楼层高度方向上分布比较均匀，没有薄弱层的存在。抗震设防烈度为8度（0.3g）时，三种地震波作用下结构沿x方向层间位移角最大值及所在楼层号见表6。

图5 8度（0.3g）罕遇地震不同地震波作用下结构沿x方向的层间位移角图

3.2.2 塑性出铰机制

由于抗震设防烈度不同时，在三种地震波作用下，P-BRW体系整体结构模型塑性铰的发展表现出大致相同的趋势，且抗震设防烈度为7度（0.1g）、7度（0.15g）或8度（0.2g）时，框架底层柱端没有出现塑性铰。所以，文章仅给出设防烈度为8度（0.3g）时，Taft波地震动作用下结构沿弱轴（x轴）方向和整体模型在8、12、15 s时的塑性铰发展情况，如图6和7所示。

表6 8度（0.3g）罕遇地震作用下结构沿x方向层间位移角最大值及所在楼层号

图6 结构x方向塑性铰发展情况图

根据图6和7可知，抗震设防烈度为8度（0.3 g）时，Taft波地震动作用下，整体结构主要通过屈曲约束钢板剪力墙的屈服耗能，与屈曲约束钢板剪力墙连接的刚接框架的梁、柱和梁端铰接框架的梁、柱在8、12 s时均保持弹性，15 s时，框架底层柱屈服，底层柱端出现塑性铰。

图7 整体结构模型的塑性铰发展情况图

在水平时程加速度作用下，整体结构模型的塑性铰率先出现在底层屈曲约束钢板剪力墙简化模型中的拉压杆上，随着时程加速度的增大和地震动的继续作用，屈曲约束钢板剪力墙简化模型中进入非线性的杆件逐渐增多，塑性铰沿楼层高度方向自下而上发展，最终使屈曲约束钢板剪力墙简化模型中的大部分拉压杆都进入屈服状态。但由于框架梁、柱仍保持弹性，屈服后的拉压杆仍可以发挥类似于支撑的功能，形成类似钢框架—支撑结构的形式，结构仍能继续承受地震力。直至在倾覆力矩和附加轴力的作用下，与拉压杆相邻的底层刚接框架柱端出现塑性铰，随后梁端铰接框架的底层柱端出现塑性铰，最终，结构达到极限承载状态，失去承载能力。

4 结论

通过上述研究可知：

（1）P-BRW体系构造简单，传力明确，在地震作用下可以最大程度的发挥屈曲约束钢板剪力墙的耗能能力，结构整体变形呈现出典型的弯曲变形特征，表现出了良好的抗侧性能。

（2）P-BRW体系结构整体模型在8度（0.2g）及以下设防烈度罕遇地震作用下，框架底层柱端没有出现塑性铰，结构最大层间位移角满足设计规范的限值要求，符合“小震不坏、中震可修、大震不倒”的设计原则。

（3）P-BRW体系结构整体模型在8度（0.3g）设防烈度罕遇地震作用下，底层柱端会形成塑性铰，不能满足“大震不倒”的抗震设防要求，表明在该截面形式下，P-BRW体系不适宜应用于8度（0.3g）及以上设防烈度的地区。

参考文献：

［1］ 贺灵童，陈艳.建筑工业化的现在与未来［J］.工程质量，2013，31（2）：1-8.

［2］ 沈祖炎，罗金辉，李元齐.以钢结构建筑为抓手推动建筑行业绿色化、工业化、信息化协调发展［J］.建筑钢结构进展，2016，18（2）：1-6，25.

［3］ 王俊，赵基达，胡宗羽.我国建筑工业化发展现状与思考［J］.土木工程学报，2016，49（5）：1-8.

［4］ 张爱林.工业化装配式多高层钢结构住宅产业化关键问题和发展趋势［J］.住宅产业，2016（1）：10-14.

［5］ 沈祖炎，李元齐.建筑工业化建造的本质和内涵［J］.建筑钢结构进展，2015，17（5）：1-4.

［6］ 周学军，王振，张慧武，等.装配式梁柱铰接钢框架——屈曲约束钢板剪力墙体系抗震性能有限元分析［J］.钢结构，2016，31（10）：20-24，79.

［7］ 郭彦林，董全利，周明.防屈曲钢板剪力墙弹性性能及混凝土盖板约束刚度研究［J］.建筑结构学报，2009，30（1）：40-47.

［8］ 郭彦林，周明.钢板剪力墙的分类及性能［J］.建筑科学与工程学报，2009，26（3）：1-13.

［9］ GB 5009—2012，建筑结构荷载规范［S］.北京：中国建筑工业出版社，2013.

［10］金双双.20层方钢管混凝土框架——钢板剪力墙结构体系抗震性能分析［D］.哈尔滨：哈尔滨工业大学，2011.

［11］侯莹莹.半刚性钢框架内填组合剪力墙混合结构抗震设计方法及塑性分析［D］.济南：济南大学，2013.

［12］Thorburn L.J.，Kulak G.L.，Montgomery C.J..Analysis of Steel Plate Shear Walls［R］.Canada：University of Alberta，1983.

［13］郭兰慧，李然，张素梅.薄钢板剪力墙简化分析模型［J］.工程力学，2013，30（S1）：149-153.

［14］Elgaaly M.，Caccese V.，Du C..Post-buckling behavior of steelplate shear walls under cyclic loads［J］.Journal of Structural Engineering，1993，119（2）：588-605.

［15］李然.钢板剪力墙与组合剪力墙滞回性能研究［D］.哈尔滨：哈尔滨工业大学，2011.

［16］李然，郭兰慧，张素梅.钢板剪力墙滞回性能分析与简化模型［J］.天津大学学报，2010，43（10）：919-927.

［17］GB 50011—2010，建筑抗震设计规范［S］.北京：中国建筑工业出版社，2016.

［18］JGJ99—2015，高层民用建筑钢结构技术规程［S］.北京：中国建筑工业出版社，2015.

（校庆约稿）

山东建筑大学工程结构与防灾减灾学科——周学军教授

周学军教授现为二级岗教授，享受国务院政府特贴专家，博士生导师，山东省结构工程省级重点学科首席专家，山东建筑大学工程结构防灾减灾及防护学科首席岗教授，山东省绿色建筑钢结构工程技术研究中心主任，国家新世纪百千万人才工程国家级人选、山东省有突出贡献的中青年专家。

周学军教授，工学博士，现兼任国家高等学校土木工程专业学科指导委员会委员、中国钢结构协会理事和专家委员专家、中国建筑金属结构协会理事及钢结构专家委员会专家、山东省高等学校土木建筑类专业教学指导委员会主任委员及山东省钢结构行业协会理事长、山东省超限建筑工程抗震审查委员会委员、国家级土木工程实验教学示范中心主任等多项社会职务、《建筑钢结构进展》和《空间结构》等学术杂志编委。

多年来从事于钢结构基本理论与空间钢结构、组合结构和装配式钢结构的教学和研究工作。出版著作11部，其中《门式刚架轻钢结构设计与施工》（山东科技出版社）被誉为我国第一本专门论述门式刚架轻钢结构设计与施工的专著，对我国轻钢结构的健康发展起到了积极的推动作用；作为主要完成人获得省部级科技奖励5项、厅局级奖励7项；参与或主持编写了国家和行业标准、地方标准10余项；在建筑结构学报、土木工程学报等国内重要学术期刊上发表学术论文120余篇；获授权专利15项；设计和审查过多项大中跨度的空间钢结构和轻型钢结构；荣获济南市“支持全运会重点工程建设特别贡献奖”。

Analysis of seismic performance of total structuremodel of P-BRW system

Zhou Xuejun1，Wang Zhen1，Xu Yuan2，et al．

（1.School of Civil Engineering，Shandong Jianzhu University，Jinan 250101，China；2.School of Engineering，Griffith University，Gold Coast4222，Australia）

The steel frame-buckling-restrained steel plate sheer wall system with pinned beam-column and consequent column is a new seismic structure.The new structure is simple and clearwhich could suit the development requirements of building industrialization.In order to study the seismic performance of this total structuremodel，the finite element analysis software was used to analyze the seismic performance of a 15-storied high-rise building under strong earthquakes with different earthquakes intensity，and got some indexes like self-vibration characteristics，hingemechanism，the curve of floor displacement and the maximum value of interlayer displacement angle.The result indicates that the beams and columns of the model remain elastic and buckling-restrained steel plate sheer wall yields rather than buckling，the system could meet the needs of seismic resistance that“Small earthquake can not damage，Moderate earthquake can repair，and Large earthquake does not fall”under the action of the rare earthquakewith the seismic fortification intensity less than or equal to 8 degrees（0.2g）.With the seismic fortification intensity to 8 degrees（0.3g），flexural plastic hinges formed at the bottom of column，which can notmeet the needs of seismic resistance.

P-BRW system；total structure model；rare earthquakes；seismic performance；finite element analysis

TU391

A

1673-7644（2016）06-0521-06

2016-10-21

国家自然科学基金项目（51308326）；山东省高校优秀科研创新团队支持计划项目（J07YA06）；山东省科技计划重点项目（2010GXZ20418）；山东省墙材革新与建筑节能科研开发项目（2014）；教育部科研创新团队支持计划项目（IRT13075）

周学军（1965-），男，教授，博士，主要从事钢结构基本理论与空间钢结构等方面的研究.E-mail：xuejunzhou@126.com