基于S型曲线的模糊故障树及其应用

徐 慧，燕雪峰

(南京航空航天大学 计算机科学与技术学院，江苏 南京 210016)

基于S型曲线的模糊故障树及其应用

徐 慧，燕雪峰

(南京航空航天大学 计算机科学与技术学院，江苏 南京 210016)

在传统模糊故障树模型综合评估中很少考虑专家可信度的影响，处理专家意见时很少考虑专家评估的可信度。文中提出基于置信度的S型曲线模糊数确定方法，引入专家权威性系数和一致性系数确定专家的置信度。运用概率偏差方法求解S型曲线的可调参数，基于可调参数和置信度来校准故障树基本事件的模糊失效概率，增加了基本事件模糊数确定的灵活性。以作战系统为例进行了实验，结果表明，针对同一基本事件各专家评估分歧较大，在各基本事件之间评估分布均匀的情况下，在未经置信处理之前各基本事件得到的最终失效概率波动比较明显，而经置信处理后的各失效概率趋于稳定，验证了改进的模糊故障树在模糊失效概率确定中结果更符合客观实际，增大了模糊故障树诊断的准确性。

模糊故障树；专家置信度；可调参数；S型曲线

1 概 述

随着现代设计、制造技术及计算机技术的飞速发展[1]，系统的结构日益复杂，对系统可靠度的需求也越来越高。故障树分析方法[2]可以用来评估一个复杂系统的安全可靠性。概率分析方法[3-4]是复杂系统可靠性分析中最常见的方法。一般组件用精确的失效概率描述它们的可靠性特征[5-6]，这需要对历史数据进行量化来确定可靠性特征。然而,在实际应用程序中很可能由于历史数据很少或者不充分而不能进行量化[7]，同时组件和基本事件的失效概率也很难推测。

针对解决一类没有确切的边界和精确的值的问题时，模糊集理论[8]已被证实是最有效的解决方法。在现实世界的领域中，历史数据很少或者不充分而不能进行量化时，只有定性数据比如专家的意见，以语言变量的形式评估系统的可靠性。此外专家更愿意用语言变量的形式评估失效，来获取不确定性的事件而不是以定量的形式去表达。

当基本事件的发生概率无法确定时，可以借助专家的知识和经验对事件的失效概率进行语言评估，并采用转换标度将语言变量转换为模糊数。不同的专家由于自身专业知识和工作经验的不同，对同一事件的评估不尽相同，需要通过一定的运算法则对专家评估意见进行处理。Hsu和Chen[4]给出了处理专家意见相似度的运算法则，但是处理时所用的计算公式相对简单且没有给出评估专家意见权重的方法。

针对专家评估问题[9]，现有文献很少考虑专家自身专业知识和工作经验对评估可信度的影响。在处理专家评估意见时，通常采用组合赋权法来确定评估的权重[9-10]，如改进的模糊层次分析法、菲尔德法消除评价误差法，同时也很少考虑专家评估的可信度。因此，文中提出了一种基于置信度的S型曲线模糊数确定模型。针对基本事件失效的可能性邀请专家评估，引入专家权威性和一致性系数来确定专家的置信度，将专家意见的统一化问题转换为求最小概率偏差问题。运用概率偏差方法求解S型曲线的可调参数，基于可调参数和置信度来校准故障树基本事件的模糊失效概率。

2 基于评价权威性和评估相似度的专家置信度确定方法

在对不同的专家评估意见进行处理时，需要进行评估综合处理。基于Chen[11]给出的一种梯形模糊数之间相似度的方法和S.M.Mir[5]等给出的风险评估方法，为了降低专家的评价误差，文中引入置信度来约束专家评价。

2.1 专家语言变量和对应的梯形模糊数

隶属度函数是模糊集的核心[12]，用来描述某个元素与模糊集的相容度。通常，三角模糊数和梯形模糊数理论中经常用到隶属度函数。一个梯形模糊数的隶属度函数被定义为：

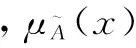
表示事件A的概率取值范围，x∈(0,1)；a1,a2,a3,a4为事件发生概率的取值范围。

专家判断以语言变量的形式表示，依据转换标度将语言变量转换为模糊失效概率，现将评语等级划分为9个等级，包括非常低VL(0 0 0.1 0.2)、较低RL(0.1 0.2 0.2 0.25)、中低ML(0.2 0.3 0.3 0.45)、低L(0.3 0.4 0.4 0.55)、中等M(0.4 0.5 0.5 0.65)、高H(0.5 0.6 0.6 0.75)、中高MH(0.6 0.7 0.7 0.85)、较高RH(0.7 0.8 0.8 0.85)、非常高VH(0.8 0.9 0.9 1.0)。

2.2 基于评价权威性的专家权威系数的确定

每一个专家对同一事件有不同的看法，和他们在各自专业领域的经验和知识有关。通过工作岗位、理论知识、专业领域、评估自信对专家评估置信度进行计算，以专家对系统掌握的信息为基础并以百分制给出定量描述来确定专家权威性系数。设评估专家有n位，每位专家的评估中，设工作岗位评分为wi，理论知识评分为li，专业领域评分为mi，评估自信评分为ci，专家i评价值为Vi。

Vi=wi·li·mi·ci,i=1,2,…,n

(1)

可得到专家i的权威性系数ri。

(2)

2.3 基于专家评价相似度的一致性系数确定方法

将各专家对各事件的失效评估意见依据转换标度转换为梯形模糊数，针对每一位专家计算专家意见的相似度。

(1)计算专家意见的相似度。

计算任意两位专家Ei和Ej对基本事件的专家意见Ai,Ai的相似度S(Ai,Aj)∈[0,1]，可以通过如式(3)计算：

(3)

其中，Ai,Ai是标准模糊数,代表专家Ei,Ej对事件的评估。

梯形模糊A=(a1,a2,a3,a4),则EV(A)定义如下：

(4)

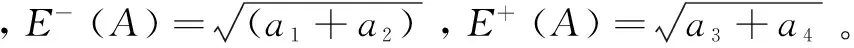
(2)计算专家Ei平均同意度AVk(Ei)。

对基本事件k构建专家意见一致性矩阵M，并计算AVk(Ei)。

(5)

其中，Sij=S(Ai,Aj)。如果i=j，则Sij=1,对基本事件k专家Ei的平均同意度AVk(Ei)为：

(6)

(3)确定专家Ei意见一致度系数σi。

(7)

其中，AVk(Ei)为第i位专家对事件k评价的一致度；m为基本事件的个数；n为专家的个数。

(4)确定专家的置信度。

基于专家自身评估意见的权威性以及同其他专家评估意见的一致性，计算得到专家置信度。选取专家评价一致性系数作为评定依据，每个专家意见的置信度为一致性系数与专家权威系数的结合。

(8)

3 基于置信度的S型曲线的拟合求解模糊数法

3.1 基于置信度的S型曲线模糊数确定模型

利用S型函数构造基于置信度的参数可调的模糊数确定模型为：

(9)

其中，f(x)是k,c的增函数,是a的减函数；可用参数a表示专家对事件评价的模糊数；参数c表示各专家的置信度；参数k用来做可调参数[9]，主要作用是校准模糊数。

3.2 基于概率偏差的可调参数求解方法

询问每位专家基本事件失效的可能性，语言变量转化为对应的模糊数得到矩阵：

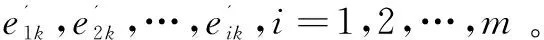
此时计算基本事件k模糊数ak1的概率偏差：

5i,j=1,2,…,m，k=1,2,…,n

(10)

调整式(9)的可调参数k，可以得到随着k取值的不同，模糊数ak1的单项概率偏差数列。同时由S型函数性质可知，函数曲线受k值影响，因此，应选择单项概率偏差序列中偏差值较小的k为模糊数确定模型中的可变参数。

X1模糊数ak1随可调参数变化的模糊数概率偏差关系见图1。

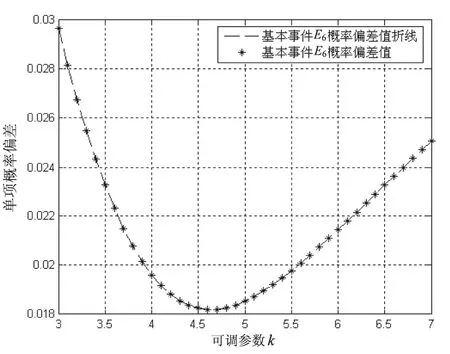
图1 X1模糊数ak1随可调参数变化的模糊数概率偏差关系图

由图1可知，固定评价者人数，单项概率偏差值取决于专家评价的相似度和差异度，曲线呈非线性变化。当可调参数k为4.7时，基本事件X1模糊数ak1偏差值最小。

3.3 基于S型曲线的模糊数求解方法

(1)对同一基本事件k，各专家的模糊评价为A1k,A2k,…,Aik,i=1,2,…,n。其中，Aik=(aik1,aik2,aik3,aik4),aik1为模糊评价数的最小可能值。将aik1及对应的可调参数k带入新的S型曲线函数，即可绘制出m条S型曲线带入新的S型曲线函数。针对aik1即可绘制出p条S型曲线，这里令x为训练数据集并取值为(0,1)。

(11)

(2)曲线拟合求解最优模糊数。对S型函数而言，任意的X对应n个f(x)值，则

(12)

训练数据集的步长s越小，中心散点集越密，曲线拟合效果越好。规定s=0.01。经过拟合得到S型曲线，得ak1反解即为该基本事件模糊数Ak中最小可能值。对该基本事件模糊数的其他最左可能值，最右可能值以及最大值分别执行步骤(1)、(2)操作，即可得到该基本事件的最终模糊数Ak。

Ak=(ak1，ak2，ak3，ak4)

(3)对其他基本事件执行以上操作，即可求得所有基本事件的模糊数。

M=(A1,A2,…,Am)

3.4 去模糊化处理

利用S型曲线可求得各基本事件最终模糊数。为了能把专家评估的将主观模糊失效概率转换为客观模糊失效概率，采用Onisawa[13]给出的一个变换函数，将主观模糊概率转换为客观模糊失效概率，有：

(13)

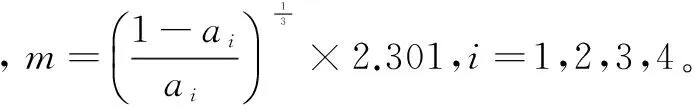
最终去模糊化处理将客观模糊失效概率转化为最终失效概率。利用Sugeno提出的中心面积法求解最终失效概率，公式为：

(14)

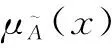
4 区域防空网络作战系统故障诊断分析

区域防空网络化作战系统[14]是防空作战能力和信息一体化相互结合的现代高科技作战系统。网络一体化防空作战系统由雷达探测预警网、拦截网、指挥控制网组成。雷达探测子系统主要由组成雷达、无线发射模块、信号接收模块、信号调制处理模块和数据处理模块组成，完成对目标信息的获取，包括目标探测和跟踪。

拦截网由防空作战平台上的硬抗击武器系统、电子战系统组成，其任务是拦截行动执行，防空导弹系统拦截作战单元对目标的拦截打击。

指挥控制子系统提供反导作战的整体控制和协调信息的发布等。

4.1 区域作战系统拦截失效故障树的模糊数确定

根据作战系统的功能，可以将目标拦截失效作为故障树的顶事件，并对该底事件进一步分析，得第一层次级事件，导弹拦截故障和指挥控制网故障。然后对次级事件进行分析，列出其相应的故障原因。综合分析建立如图2所示的故障树。

在对故障树中基本事件发生可能性评估之前，需要对专家评估的权威性进行处理。考虑专家对评审内容的权威程度[9]，从工作岗位、知识理论、专业领域、评估自信等对专家评价可信度进行分析，专家权威评价表如表1所示。

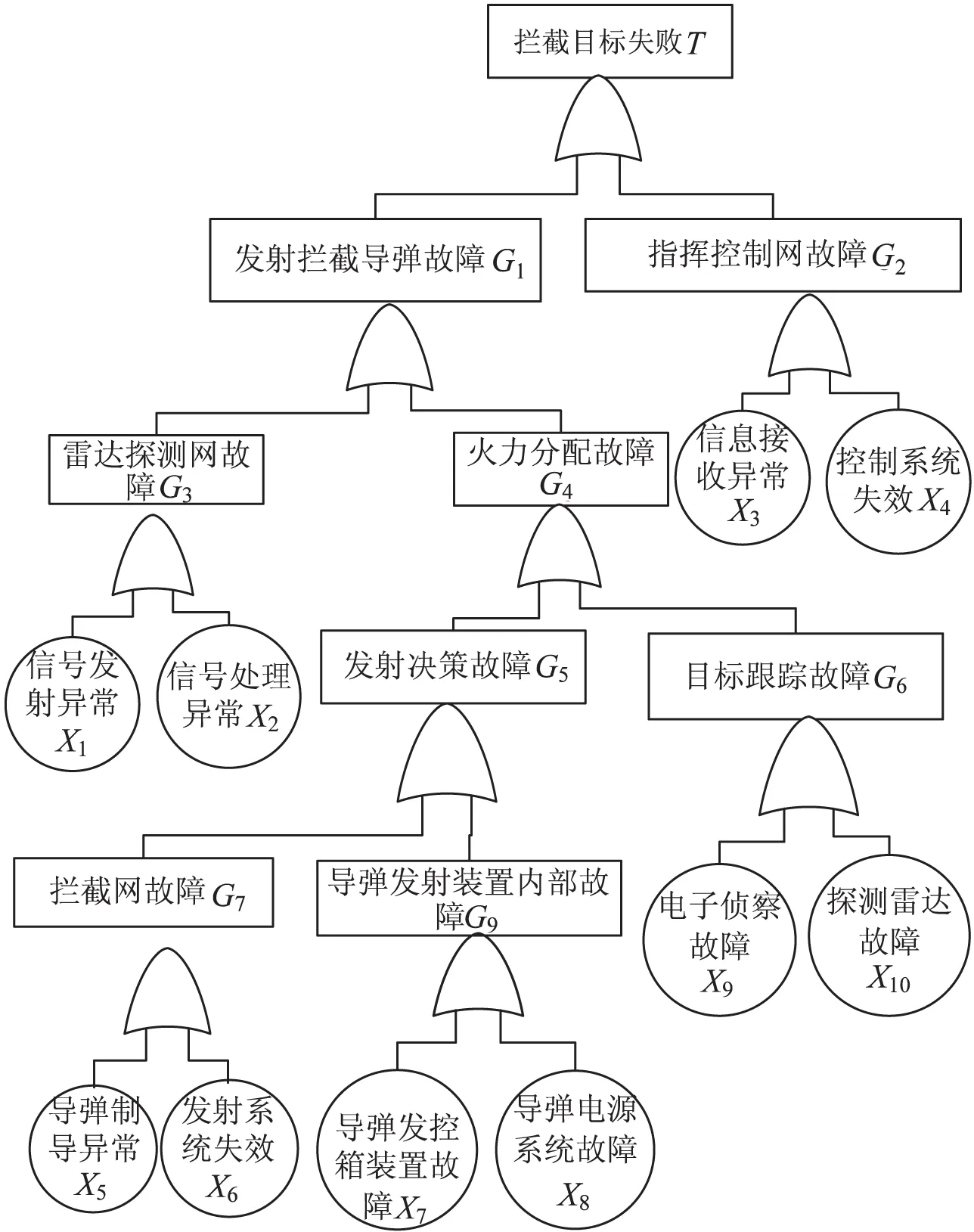
图2 拦截失败故障树

E1E2E3E4E5工作岗位908010090100知识理论9090807080专业领域7080809070评价自信80909010080

邀请专家对基本事件做出模糊判断，得到基本事件的模糊概率评价，如表2所示。

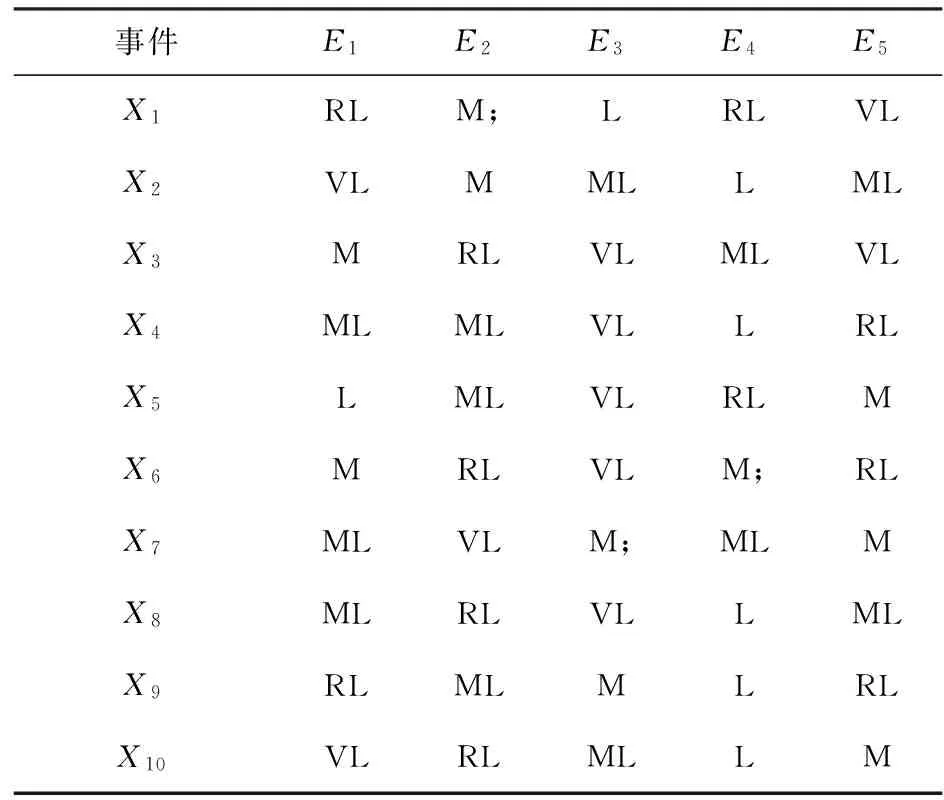
表2 基本事件的专家评估表

由表1表2和式(1)-(7)可得专家评估权威性系数和专家置信度。将表3中各专家的评估意见转化为对应的模糊数可求得未经处理的各基本事件的模糊数。应用式(8)-(12)计算各基本事件对应的可调参数k和对应的模糊数。经解得X1的a1=0.239,同理对a2,a3,a4拟合求解得0.321，0.367，0.452。对所有的基本事件拟合求解，经计算可得所有基本事件的最优模糊数。未经处理求得的所有基本事件模糊数和经过S型曲线拟合求解得到的模糊数如表3所示。

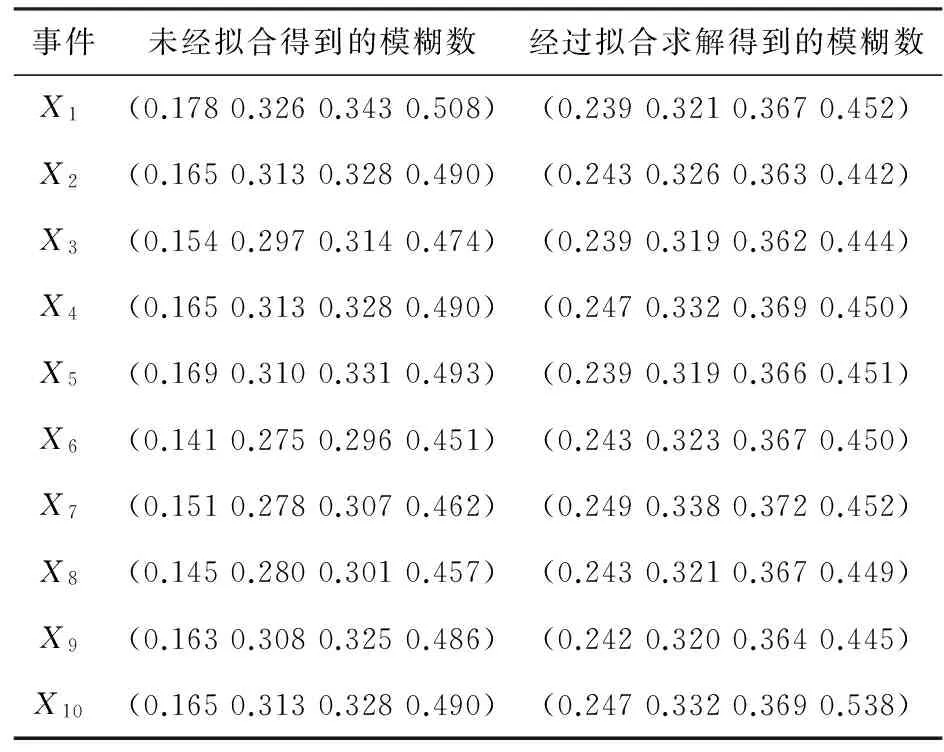
表3 未经拟合和经过拟合求解得到的基本事件模糊数对比表

4.2 结果分析

由于专家自身专业知识和工作领域的不同，对事件的评估具有差异性，为了使专家的评价客观可信，有必要对专家评价置信度进行分析。对置信处理前得到的基本事件模糊数和置信处理后得到的模糊数去模糊化后得到各基本事件对应的失效概率并进行对比，如图3所示。

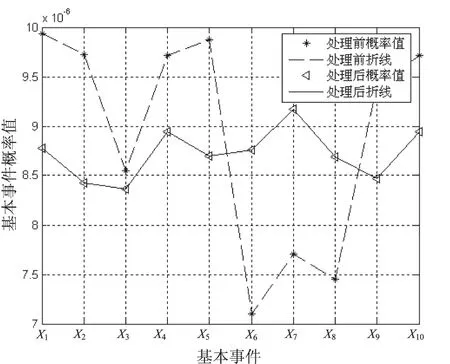
图3 置信处理前后基本事件失效概率对比图

由图3可知，针对同一基本事件各专家评估分歧较大，而在各基本事件之间评估分布均匀的情况下，在未经置信度处理之前各基本事件得到的最终失效概率波动比较明显，而经置信处理后的各失效概率趋于稳定。经过拟合求解可得各基本事件失效概率大小排序情况与作战系统拦截失效故障树中各基本事件失效可能性大小相符，表明该模型有效、可行。专家评估过程是一个动态变化的过程，随着评价者人数及外在环境的变化，各基本事件之间失效可能性的差异会发生变化。针对动态评价过程中各基本事件波动变化明显的情况，可采用S型曲线拟合的方法来统一专家意见。

5 结束语

针对传统模糊故障树在处理专家评估意见的重要程度和基本事件最终模糊数的确定时所用的理论公式比较简单，同时也未考虑专家评估意见的可信度。文中提出了基于置信度的S型曲线模糊数确定模型，在处理专家意见分歧较大时，用S型函数处理拟合求解各基本事件的模糊失效概率。最终计算得到各基本事件的失效概率和各基本事件在故障诊断中的重要性，便于在不确定条件下找出导致故障发生的主要原因，增加了模糊失效概率确定的灵活性。

[1] Purba J H,Lu J,Zhang G,et al.A fuzzy reliability assessment of basic events of fault trees through qualitative data processing[J].Fuzzy Sets & Systems,2014,243:50-69.

[2] Huang H Z,Tong X,Zuo M J.Posbist fault tree analysis of coherent systems[J].Reliability Engineering & System Safety,2004,84(2):141-148.

[3] Purba J H.Fuzzy probability on reliability study of nuclear power plant probabilistic safety assessment:a review[J].Progress in Nuclear Energy,2014,76:73-80.

[4] Hsu H M,Chen T C.Aggregation of fuzzy opinion under group decision making[J].Fuzzy Sets and Systems,1994,79:279-285.

[5] Miri Lavasani S M,Yang Z,Finlay J,et al.Fuzzy risk assessment of oil and gas offshore wells[J].Process Safety and Environmental Protection,2011,89:277-294.

[6] An M.Risk assessment in railway safety management[J].International Journal of Engineering and Technology,2007,14:45-56.

[7] Pillay A,Wang J.A risk ranking approach incorporating fuzzy set theory and grey theory[J].Engineering Reliability & System Safety,2003,79(1):61-67.

[8] Wang D,Zhang P,Chen L.Fuzzy fault tree analysis for fire and explosion of crude oil tanks[J].Journal of Loss Prevention in the Process Industries,2013,26(6):1390-1398.

[9] 何 逢,燕雪峰,周 勇.基于S型曲线的指标权重确定方法[J].计算机科学,2015,42(6):216-219.

[10] 徐晓燕,刘 琴.改进的模糊故障树在农村BOT项目风险评估中的应用[J].西北工业大学学报：社会科学版,2014,34(1):73-79.

[11] Chen S.A new similarity measure of generalized fuzzy numbers based on geometric-mean averaging operator[C]//Proc of IEEE international conference on fuzzy systems.Vancouver,BC,Canada:Institute of Electrical and Electronics Engineers Inc.,2006:1879-1886.

[12] 黄文静.概率模糊集理论研究及其建模[D].长沙:中南大学,2013.

[13] Onisawa T.An approach to human reliability in man-machine systems using error possibility[J].Fuzzy Sets and Systems,1988,27:87-103.

[14] 陈志航,黄武超,李中良.舰艇编队网络一体化反潜作战体系研究[J].舰船电子工程,2010,30(8):1-3.

Fuzzy Fault Tree and Its Application Based on S Curve

XU Hui，YAN Xue-feng

(School of Computer Science and Technology，Nanjing University of Aeronautics & Astronautics, Nanjing 210016,China)

Aiming at the problem of the comprehensive evaluation of the traditional fuzzy fault tree model,the reliability of the expert evaluation is seldom considered in the process of dealing with the expert opinion.Fuzzy number determination method based on the confidence degree of S type curve is proposed,introduction of the expert’s authority coefficient and the consistency coefficient.The probability deviation method is used to get the adjustable parameters of the S type curve,and the fuzzy failure probability of the basic events for the fault tree can be calibrated based on the adjustable parameters and the confidence level.Experiments are carried out in the combat system,whose results show that the assessment of the same basic events is quite different when the assessment of the distribution of the basic events is even,the final failure probability of each basic event is more obvious,and the probability of failure probability is more stable and verified that improved fuzzy fault tree is more consistent with the objective reality,and the accuracy of the fuzzy fault tree diagnosis is increased.

fuzzy fault tree；expert confidence degree；adjustable parameter；S type curve

2015-09-28

2015-12-30

时间：2016-05-25

国防科工局“十二五”重大基础科研项目(0420110005)

徐 慧(1989-)，女，硕士研究生，研究方向为系统建模与仿真；燕雪峰，教授，研究方向为复杂系统仿真、分布交互仿真等。

http://www.cnki.net/kcms/detail/61.1450.TP.20160525.1711.066.html

TP391.9

A

1673-629X(2016)06-0001-05

10.3969/j.issn.1673-629X.2016.06.001