基于压缩感知的自适应导频信道估计
2016-02-27孙君,高杰
孙 君,高 杰
(南京邮电大学 通信与信息工程学院,江苏 南京 210003)
基于压缩感知的自适应导频信道估计
孙 君,高 杰
(南京邮电大学 通信与信息工程学院,江苏 南京 210003)
在无线通信系统中,如何提升信道估计的准确度对提升无线通信的系统性能至关重要。在信道估计中,导频开销占据了较多的频谱资源,且传统的信道估计算法不能根据信道状态实时调整信道估计中所需要的导频数量。而压缩感知信道估计算法,可以利用无线信道的稀疏特性,提高信道估计的精确度,减少导频子载波的开销。基于此特点,将压缩感知与信道估计相结合,研究了基于压缩感知的稀疏度未知情况的信道估计,并提出一种适用于LTE-A系统的导频自适应信道估计算法。仿真结果表明:与传统的LS信道估计和LMMSE信道估计相比,所提出的导频自适应算法能够将导频数量减少40%左右,并能获得更准确的信道估计性能。
压缩感知;信道估计;自适应;导频
1 概 述
作为第四代移动通信的代表,LTE-A采用了正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)等关键物理层传输技术。虽然针对于LTE-A系统的研究已经趋近成熟,但是LTE-A信道估计技术仍然是一个主要的研究问题。OFDM技术虽然能够有效解决多径效应和信道频率选择特性的问题,但在接收端OFDM需要通过精确的信道状态信息进行相干解调,因此精确的信道估计在OFDM系统中起着举足轻重的作用[1]。研究表明[2],高速宽带无线通信中由于多径效应的影响,信号的能量将集中在无线信道主要的几条可分辨路径中,在时域上具备稀疏特性。
在传统的信道估计中,诸如最小二乘法(Least Square,LS)和线性最小均方误差(Linear Minimum Mean Square Error,LMMSE)以及维纳滤波等典型的信道估计技术[3-5],都利用了导频信息对信道进行估计,且都没有考虑到信道的稀疏特性。随着近几年压缩感知理论[6-7]的兴起,利用信道的稀疏特性进行信道估计成为通信领域的一个研究热点。对于稀疏信道,压缩感知的引入不仅可以降低导频开销,同时也能够更准确地获得信道状态信息。
针对于压缩感知在信道估计中的应用,已经有很多学者对此进行了研究。文献[8]研究了信道稀疏度已知条件下OFDM系统的稀疏信道估计算法。但在实际信道中稀疏度是未知的,文献[9]提出一种稀疏度自适应匹配追踪算法(Sparsity Adaptive Matching Pursuit,SAMP),能够在稀疏度未知的情况下获得当前信号的稀疏度并精确重构原始信号。传统的信道估计中,诸如LS和LMMSE算法在导频点均匀分布的时候能够取得最优的信道估计性能。而在压缩感知理论中,随机分布的采样点才能够取得最优的重构性能。文献[10-11]对压缩感知信道估计中导频子载波的位置进行了研究。
在现有研究的基础上,文中提出了一种基于压缩感知的导频自适应信道估计算法。在信道稀疏度未知的情况下,首先通过压缩感知算法估计当前信道的稀疏度和信道状态信息,然后自适应调整下一帧传输信号的导频密度信息。与现有研究中导频密度在信号传输开始时就已经设定且保持固定不同,文中提出的自适应导频信道估计能够根据前一帧反馈的信道状态信息,更加灵活地调整下一帧中所需要的最小导频密度,减少不必要的导频开销。仿真结果表明,与现有方法对比,通过使用导频自适应算法,在降低导频开销的同时能够获得更精确的信道估计性能。
2 压缩感知和系统模型
2.1 压缩感知
压缩感知(Compressive Sensing)理论[12-14]的主要思想是利用信号的稀疏性以远低于奈奎斯特采样率的采样方式对信号进行采样,并通过重构算法实现对原始信号的精确重构。压缩感知问题可以归结为对式(1)中的x进行求解:
y=Φx=Φ(Ψα)
(1)
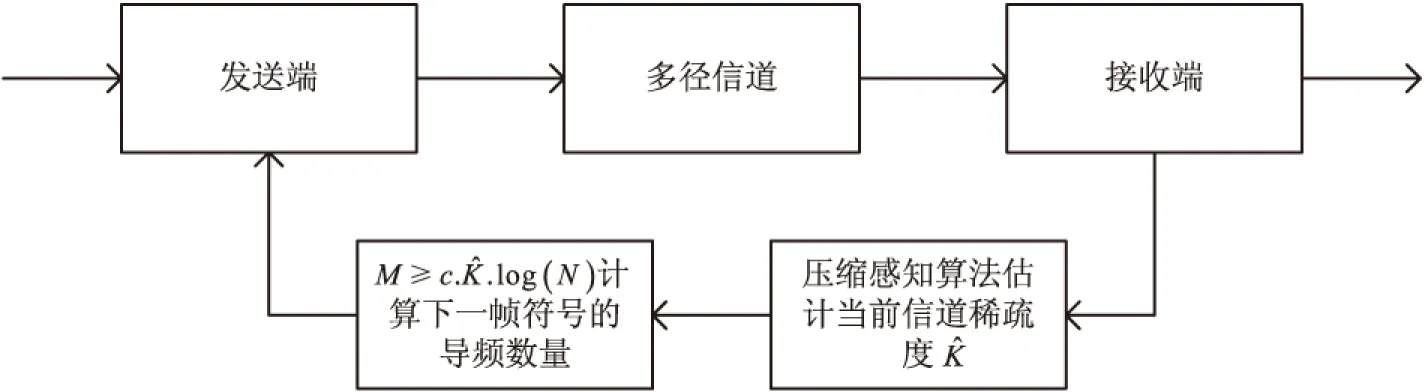
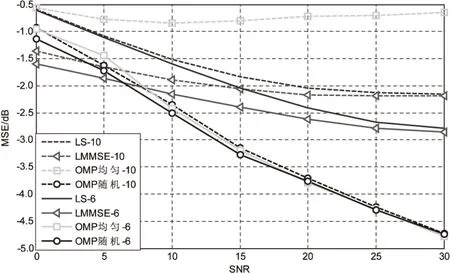
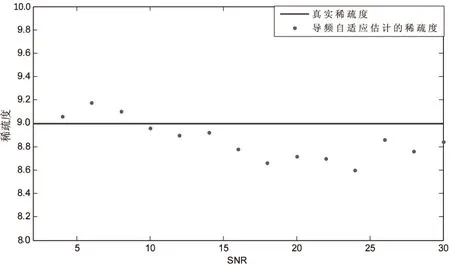
其中,x为N×1维的稀疏信号向量,在N×N维稀疏基Ψ上可以稀疏表示,其稀疏度为K;y为M×1维的观测值;Φ为M×N维的观测矩阵;K 压缩感知的基本问题主要包括以下三个方面:信号的稀疏表示;观测矩阵的设计;信号的重构算法,即如何从观测值y中恢复信号x。 式(1)中,未知数的个数远大于方程的个数。为实现信号的精确重构,对于满足‖x‖0≤K的x,观测矩阵Φ必须满足约束等距(RestrictedIsometryProperty,RIP)[6]准则: (2) 从观测值y中恢复信号x的问题,可以转化为基于0-范数的最优化求解问题: min‖ΦTx‖0s.t.y=Φx (3) 式(3)是一个基于0-范数的非凸优化问题。由于0-范数问题是无解的,在实际中0-范数问题被转化为可解的l-范数的凸优化问题。对于式(3)的求解过程就是压缩感知的重构过程。常见的重构算法[6]有基追踪(BasisPursuit,BP)、正交匹配追踪算法(OrthogonalMatchingPursuit,OMP)以及SAMP等典型算法。考虑到算法复杂度和信号重建的性能,OMP算法在信道估计中应用的更为广泛。 2.2 系统模型 (4) Yp=XpH+Np=XpFph+Np (5) 其中,Yp、Xp、Np和Fp分别表示导频位置的接收值、发送值、信道加性噪声和导频位置相对应的FFT矩阵的行向量。 根据式(5)可以获知导频处的频域信道冲击响应: (6) 式(6)可以通过压缩感知的重构算法对信道的时域冲击响应值h进行求解。 3.1 算法描述 在传统的信道估计中,导频的数量和模式都是预先设定,以保证在信道环境较差时依然能获得较好的信道估计性能。但这种预设的导频并不能根据信道环境的变化调整导频密度,导致信道环境较好时存在过多的频谱资源用于不必要的导频传输。 针对传统信道估计的这一缺点,文中提出一种导频自适应的压缩感知信道估计方法,可以在信道稀疏度未知的情况下对信道做准确估计并指示下一帧的导频密度,从而在降低导频开销的同时提升信道估计性能。其主要思想就是根据信道稀疏度的变化,实时调整下一帧信号中所需要的导频数量。图1给出了所提算法的基本流程。 图1 基于压缩感知的导频自适应信道估计的基本过程 首先,接收端接收到第N-1帧信号后,提取当前帧的导频信息,根据LS算法获得当前子帧的导频位置的频域响应值;其次,在信道稀疏度未知的情况下,通过压缩感知的重构算法估计当前子帧的信道稀疏度和信道状态信息;最后,根据估计得到的信道稀疏度评估当前信道状况,并根据式(7)计算下一帧信号所需要的最小导频密度,并反馈给发送端。 根据文献[6],要想精确地从采样值中重构原始信号,测量值的维度必须满足: (7) 其中,N为已知量;K则由压缩感知的重构算法获得。 3.2 SAMP算法 文中采用文献[9]中的SAMP算法,在信道稀疏度未知的情况下估计信道稀疏度。基本过程如下: 首先,对信道残差r(观测值与观测值之间的差值)、支撑索引集Λ和候选集C、迭代次数i和阶段stage进行初始化。其中,r0=Yp,Λ=∅表示每次迭代中与接收值Yp相关性较大的观测矩阵的索引,C=∅表示每阶段与接收值Yp相关性较大的观测矩阵的索引,i=stage=1;循环过程如下: Step1:计算残差与观测矩阵每一列Aj的内积〈Aj,ri-1〉,选取内积最大的s个值的索引记为Js; Step2:更新候选集Ci=Λi-1∪Js; Step4:判决是否‖ri‖≤ε,如果是则跳出循环;否则判断是否‖ri‖≥‖ri-1‖,是则更新stage=stage+1,k=stage×s,否则Λi=Λ,i=i+1。 本节通过蒙特卡罗仿真验证分析所提算法的性能,并给出仿真结果分析。仿真参数设置如下:OFDM符号子载波数为1 024,采用3GPP协议36.101中的EVA信道,循环前缀长度160,采用QAM调制,并选取导频间隔为6作为标准的导频参考,对于每个符号进行600次仿真。仿真中分别以LS、LMMSE和信道稀疏度已知的OMP重构算法作为对比。 图2主要分析了不同导频模式下的信道估计性能随信噪比(SignalNoiseRatio,SNR)变化的均方误差(MeanSquareError,MSE)曲线。图中实线表示导频间隔为6时的性能曲线,虚线表示导频间隔为10时的性能曲线(根据式(7)中c的取值不同而略有不同,此处c为1.65)。 图2 不同导频模式下的MSE曲线 从图中可以得知,LS、LMMSE的估计性能随着导频数量的减少而大幅降低。与此同时,采用随机导频模式的OMP重构算法进行的信道估计性能保持不变,而采用均匀导频模式的OMP算法,在不同导频间隔时性能差距较大。由分析可知,在导频间隔为10时,导频数量仍然能够满足式(7)的要求;采用均匀导频模式时,导频间隔为10时所选用的测量矩阵的相关性较大,从而降低了信道估计的性能。 图3给出了不同信噪比下导频自适应算法信道估计性能。图中OMP采用随机的导频模式,LS和LMMSE算法采用均匀导频模式。 从仿真结果可以看出,导频自适应算法根据前一帧估计的稀疏度,及时调整当前帧的密度减小导频开销的同时,能够达到与稀疏度已知的OMP算法近乎一致的性能。 图4给出了导频自适应算法估计的信道稀疏度与真实稀疏度对比的情况。 图3 导频自适应算法性能 图4 不同SNR下的稀疏度估计性能 文中主要研究了一种导频自适应的压缩感知信道估计算法。该算法通过一种反馈机制实时反映当前信道状态,为下一帧信号的导频设计提供最优方案,在减少导频数量的同时降低信道估计误差,提升信道估计的准确度。仿真结果表明,与传统的信道估计所需导频数量相比,导频自适应的压缩感知信道估计算法能够减少40%左右的导频开销。 [1]GhassemiA,GhasemnezadH,GulliverTA.CompressivesensingbasedestimationofOFDMnonlineardistortion[C]//Procof2014IEEEinternationalconferenceoncommunication.[s.l.]:IEEE,2014:5055-5059. [2] 赵 竞,王 玲.压缩感知理论在OFDM稀疏信道估计中的应用[J].通信技术,2012,45(3):13-15. [3] 张继东,郑宝玉.基于导频的OFDM信道估计及其研究进展[J].通信学报,2003,24(11):116-124. [4] 王东明,高西奇,尤肖虎,等.宽带MIMO-OFDM系统信道估计算法研究[J].电子学报,2005,33(7):1254-1257. [5]HoeherP,KaiserS,RobertsonP.Two-dimensionalpilotsymbolaidedchannelestimationbyWienerfiltering[C]//ProcofIEEEinternationalconferenceonacoustics,speech,andsignalprocessing.[s.l.]:IEEE,1997:1845-1848. [6] 于华楠,郭树旭.基于压缩感知的超宽带信道估计方法的研究[J].电子与信息学报,2012,34(6):1452-1456. [7] 焦东立,朱立东.一种基于压缩感知的信道估计算法[J].空间电子技术,2011,8(3):16-19. [8]TaubockG,HlawatschF,EiwenD,etal.Compressiveestimationofdoublyselectivechannelsinmulticarriersystems:leakageeffectsandsparsityenhancingprocessing[J].IEEEJournalofSelectedTopicsinSignalProcessing,2010,4(2):255-271. [9]DoTT,LuG,NguyenN,etal.Sparsityadaptivematchingpursuitalgorithmforpracticalcompressedsensing[C]//Procof2008 42ndAsilomarconferenceonsignals,systemsandcomputers.CA,PacificGrove:[s.n.],2008. [10]ApplebaumL,BajwaWU,CalderbankAR,etal.DeterministicpilotsequencesforsparsechannelestimationinOFDMsystems[C]//Procof2011 17thinternationalconferenceondigitalsignalprocessing.Corfu:[s.n.],2011. [11]SharpM,SacglioneA.Ausefulperformancemetricforcompressedchannelsensing[J].IEEETransactionsonSignalProcessing,2011,59(6):2982-2988. [12]CandesE,TaoT.Nearoptimalsignalrecoveryfromrandomprojections:universalencodingstrategies[J].IEEETransactionsonInformationTheory,2006,52(12):5406-5425. [13] 石光明,刘丹华,高大化,等.压缩感知理论及其研究进展[J].电子学报,2009,37(5):1070-1081. [14] 戴琼海,付长军,季向阳.压缩感知研究[J].计算机学报,2011,34(3):425-434. Adaptive Pilot Channel Estimation Based on Compressive Sensing SUN Jun,GAO Jie (School of Communication and Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China) In wireless communication system,how to improve the accuracy of channel estimation is very important for improvement of the performance for wireless communication system.In the channel estimation,the pilot overhead occupies a large amount of spectrum resources,and the traditional channel estimation algorithm cannot adjust the pilot channel estimation according to the channel state.The compressed sensing channel estimation algorithm,taking advantage of the sparse characteristic of wireless channel,improves the accuracy of channel estimation and decreases the pilot overhead.Based on these features,combined compressive sensing with channel estimation,investigating channel estimation with unknown channel sparsity based on compressive sensing,an adaptive pilot channel estimation algorithm is put forward for LTE-Advanced systems.Simulation shows that compared with the traditional LS and LMMSE,it can reduce the number of pilot by 40% and obtain more accurate channel estimation performance. compressive sensing;channel estimation;adaptive;pilot 2015-12-04 2016-03-09 时间:2016-08-01 国家“863”高技术发展计划项目(2005AA121620,2006AA01Z232);江苏省普通高校研究生科研创新计划资助项目(CX07B_110z);南邮校级项目(NY211033) 孙 君(1980-),女,硕士研究生导师,研究方向为无线通信;高 杰(1989-),男,硕士研究生,研究方向为移动通信与无线通信。 http://www.cnki.net/kcms/detail/61.1450.TP.20160801.0907.048.html TP301 A 1673-629X(2016)10-0184-04 10.3969/j.issn.1673-629X.2016.10.040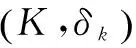
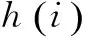
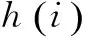
3 导频自适应的压缩感知信道估计

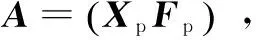
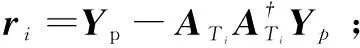
4 仿真结果与分析

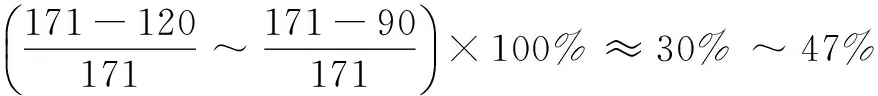
5 结束语
