命制新型不等式试题的几种方法*——对不等式sinx＜x＜tanx，x∈（0，）的再构造

☉江西省九江第一中学 江民杰

命制新型不等式试题的几种方法*

☉江西省九江第一中学 江民杰

函数、导数、不等式属中学数学核心内容之一，是高考数学试题的重点考查对象，特别是涉及不等式的函数问题，更是重中之重.我们研究此类试题解法的同时，心里总有一个想法：该不等式是如何构造出来的？即站在全局的高度，研究试题命制的心路历程，探明试题的来龙去脉，解密数学试题的命题背景，进而达到：能从教材最基础的概念、定理、公式出发，整合相关知识点及方法，对概念、定理、公式进行提升，进而命制较高要求的能力型数学试题.限于篇幅，我以不等式“sinx＜x＜tanx， x∈（0，）”为载体，探讨命制新型不等式的方法.

一、利用不等式自身变形

分析：f′（x）＝cosx-xsinx-acosx＝（1-a）cosx-xsinx，

综上所述，实数a的取值范围为a≥1.

这种处理及命题技术在高考试题中经常使用，如：

（2014北京理科18）已知函数f（x）＝xcosx-sinx，x∈

（Ⅰ）求证：f（x）≤0；

二、利用两函数复合

利用两个函数复合，可以产生新的函数不等式.

新题（二）已知a＞0，f（x）＝x+xcosx-asinx＜0在x∈（0，π）上恒成立，求实数a的取值范围.

分析：f（x）＝x（1+cosx）-asinx＜0在x∈（0，π）上恒成立⇔0在x∈（0，π）上恒成立.

又x∈（0，π），则φ（x）＞φ（0）＝0，符合题意.

记cosx0＝a-1，因为cosx在（0，π）上单调递减，所以当x∈（0，x0）时，a-1＝cosx0＜cosx＜1，所以a-1-cosx＜0.所以在x∈（0，x）上单调0递减.

所以当x∈（0，x0）时，φ（x）＜φ（0）＝0，不符合题意.

综上所述，实数a的取值范围为a≥2.

三、利用积分

在原不等式两边取变上限积分，可以构建新的不等式.

新题（三）（fx）＝1-cosx-ax2＜0在x∈（0，）上恒成立，求实数a的取值范围.

分析：f′（x）＝sinx-2ax，f″（x）＝cosx-2a.

当x∈（0，x0）时，2a＝cosx0＜cosx＜1.

所以f″（x）＝cosx-2a＞0.所以f′（x）在（0，x0）上单调递增.

所以f′（x）＞f′（0）＝0.所以f（x）在（0，x0）上单调递增.

所以由x∈（0，x0）知，f（x）＞f（0）＝0，不符合题意.

当a≤0时，f′（x）＝sinx-2ax＞0，所以（fx）在（0，）上单调递增.

四、对变量进行赋值

通过对变量进行赋值，累加可以产生数列型不等式.

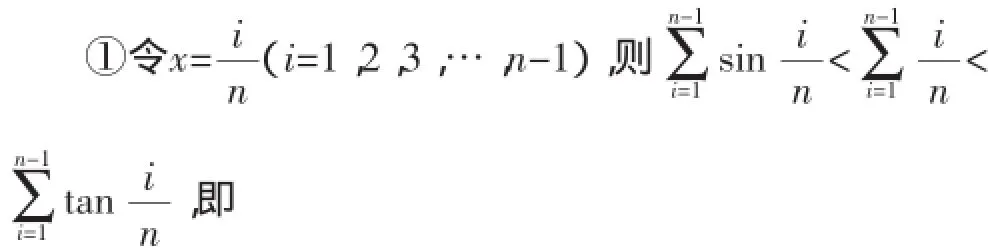
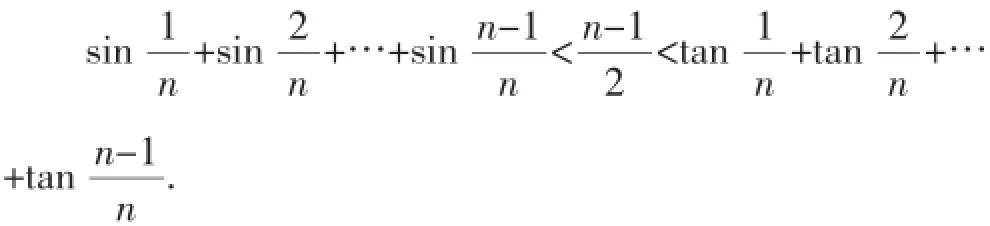
由此可以编拟下列不等式：

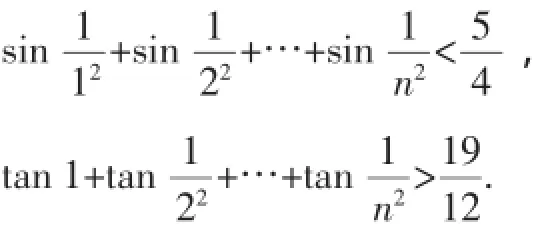
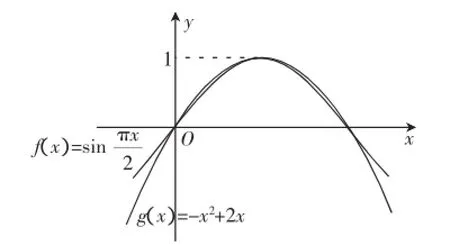
五、利用公切线

利用两曲线公共点处存在公切线，结合图像，可以构建不等式.

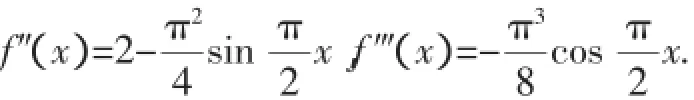
21（fx1）＞0.而x∈（0，x）1时，f（′x）连续且（f0）＜0，（fx）1＞0.故存在x2∈（0，x1），使得f（′x2）＝0.

此时，由f′（x）的单调性知，当x∈（0，x2］时，f′（x）≤f′（x）2＝0，故（fx）在（0，x2］上为减函数.故（fx）＜（f0）＝0；x∈［x2，x1］时，f′（x）＞f′（x2）＝0，此时（fx）为增函数，而x∈［x1，1）时，f′（x）＞f′（1）＝0，此时f（x）为增函数，故（fx）在［x2，1）上为增函数，故（fx）＜（f1）＝0.

综上所述，x∈（0，1）时，（fx）＜0.

故f"（x）在（0，1）上单调递减.

六、利用对称性

分析：应用几何画板画出f（x）＝x2-2x+sinx，x∈（-1，1）的图像，可以发现其极值点向左偏移，利用对称性，进而命制下面试题.

新题（六）（江西省八所重点中学2015届高三联考）已知（fx）＝x2-2x+sinx，x∈（-1，1），记（fx）的极小值为f（x0）.若f（x1）＝f（x2），求证：x1+x2＞2x0.

证明：f（x）＝x2-2x+sinπ 2x，x∈（0，1），f′（x）＝2x-

令φ（x）＝f′（x），x∈（0，1），φ′（x）＝2-sin，显然φ′（x）在区间（0，1）单调递减.

所以φ（x）在（0，ξ）上单调递增，在（ξ，1）上单调递减，即f′（x）在（0，ξ）上单调递增，在（ξ，1）上单调递减.又 f′（0）＝-2+＜0，f（′1）＝0，所以f（′ξ）＞0.由f（′x）＝0，知0＜

0x0＜ξ＜1.

所以f（x）在（0，x0）上单调递减，在（x0，1）上单调递增.

不妨设x1＜x2，由f（x1）＝f（x2），则0＜x1＜x0＜x2＜1.

令F（x）＝f（x0+x）-f（x0-x），

则F′（x）＝f′（x0+x）+f′（x0-x）

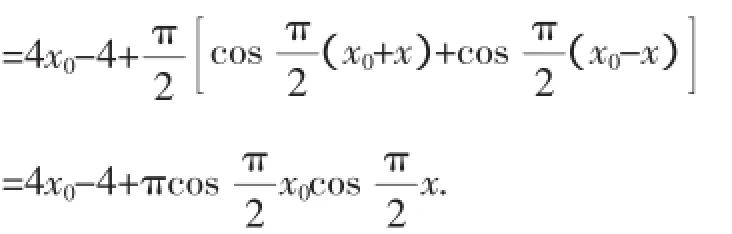
又F′（x）在x∈（0，1）上单调递减，所以F′（x）＜F′（0）＝

所以F（x）在x∈（0，1）上单调递减.所以F（x）＜F（0）＝0，

即f（x0+x）＜f（x0-x）.

又f（x1）＝f（x2）＝f［x0-（x0-x2）］＜f［x0+（x0-x2）］＝f（2x0-x2），

0＜x1＜x0，-1＜-x2＜2x0-x2＜x0，

又f（x）在（0，x0）上单调递减，且f（x）在（-1，0）上单调递减，故f（x）在（-1，x0）上单调递减.

所以x1＜2x0-x2.所以x1+x2＞2x0.

七、利用割线

利用割线与曲线的上下位置关系，可以构建不等式.

【12全国大纲理20】设函数f（x）＝ax+cosx，x∈［0，π］.

（Ⅰ）讨论f（x）的单调性；

（Ⅱ）设f（x）≤1+sinx，求a的取值范围.

八、利用距离

利用两点间的距离及点到直线的距离可以构建不等式.

g（x）＝x+sin2x-，故g（x）表示P（x，sinx），两点间的距离.其中，P（x，sinx），分别在函数y＝sinx的图像上，令，故|PQ|的最小值就是的距离.于是可以得到不等式：（x-a）2+

*本文系江西省教研室重点课题“高考数学命题与数学教材关系研究”的系列成果之一.