基于改进蜂群算法的数字信号调制识别

吴少华，单剑锋

(南京邮电大学 电子科学与工程学院，江苏 南京 210000)

基于改进蜂群算法的数字信号调制识别

吴少华，单剑锋

(南京邮电大学 电子科学与工程学院，江苏 南京 210000)

针对传统人工蜂群(ABC)算法初始种群在解空间分布不均匀、收敛速度慢等缺点，文中提出一种基于二维均匀设计和欧氏距离的改进蜂群算法。改进蜂群算法在构造初始食物源时采用二维均匀设计使食物源在解空间均匀分布，提高了算法的全局搜索能力；在构造新食物源时采用欧氏距离法提高了算法的寻优效率。文中利用信号二阶以上累积量可以抑制噪声影响的特性，从二阶、四阶和六阶累积量中提取四个特征参数作为特征向量，采用支持向量机分类器，并用改进蜂群算法对支持向量机的惩罚因子和核函数参数进行优化，实现了2FSK、BPSK、QPSK、16QAM、64QAM五种调制方式的分类识别。仿真结果表明，改进蜂群算法具有更快的收敛速度，且改进ABC-SVM方法在信噪比-3 dB时具有更好的识别效果，平均识别率为92.9%；当信噪比超过4 dB时，改进ABC-SVM方法平均识别率达到99%。

人工蜂群；欧氏距离；二维均匀设计；支持向量机；调制识别

0 引 言

随着通信技术和国民经济的发展，数字信号的自动识别在民用和军事领域被广泛应用。在日趋复杂通信环境中，通信信号调制方式的识别仍是认知无线电、频谱监测与管理、通信对抗等领域的重要研究课题。

通信信号的调制识别方法主要分为两大类：判决理论识别方法和统计模式识别方法。前者采用概率论和假设检验理论来解决信号分类问题；后者首先将接收信号映射到特征域，然后利用模式识别方法确定判决域。统计模式识别方法主要分为两个部分：特征提取和分类器。对于特征提取，目前主要采用的方法有提取信号瞬时频率、瞬时相位以及功率谱密度、小波变换、原点矩、累积量等方法[1-4]。对于分类器，支持向量机(Support Vector Machines,SVM)分类器由于其能有效解决小样本、高维数及局部最优等问题而被广泛采用。

人工蜂群(Artificial Bee Colony,ABC)算法是一种基于蜜蜂种群智能行为的优化算法，由Karaboga在2005年提出。算法简单易用、控制参数少、鲁棒性强，适用于对复杂优化问题进行求解[5]。文献[6]将人工蜂群算法应用于支持向量参数的优化，与粒子群算法和遗传算法进行了比较，获得更高的分类准确率。文献[7]将蜂群算法与支持向量机相结合，在实测轴承故障信号的识别中获得99.1%的准确率。然而，传统的人工蜂群算法仍存在着种群多样性差、搜索速度慢、易陷入局部最优等缺陷。文献[8]引入小生境技术，解决了人工蜂群算法早熟收敛、搜索速度较慢等问题。文献[9]将混沌思想引入ABC算法中，利用混沌的随机性和遍历性提高算法的全局搜索能力。文献[10]引入OBL策略产生新食物源取代每次迭代的最差食物源,并结合NIT技术提出一种多峰优化方法。

文中采用人工蜂群算法对支持向量的参数进行优化，并结合支持向量机所需优化参数为两个的事实，对人工蜂群算法进行改进。在种群初始时，采用二维均匀设计理论，使初始食物源更均匀分布在解搜索空间；在构建新食物源时，提出一种基于欧氏距离的觅食方法以改进种群局部和全局的更新策略。

1 信号和特征提取

文中研究的信号的调制方式分别是2FSK、BPSK、QPSK、16QAM、64QAM。考虑到信号的高阶累积量包含了信号的调制信息，且二阶以上的累积量能消除高斯噪声的影响，具有良好的抗噪声能力，因此文中以二阶、四阶和六阶累积量为基础进行特征提取。

1.1 信号模型

设接收信号的模型为：

式中，k=1,2,…,N，N为发送码元序列的长度；ak为发送码元序列；x(t)为发送码元波形；Ts为码元宽度；fc为载波频率；θc为载波相位；E为信号能量；n(t)是与发送信号s(t)独立的零均值的复高斯白噪声。

1.2 高阶累积量

k阶平稳随机过程{x(t)}的k阶累积量定义为[11]：

Ckx(τ1,τ2,…,τk-1)=

Cum(x(t),x(t+τ1),…,x(t+τk-1))

(2)

对于一个零均值的复平稳随机工程X(t)，定义p阶混合矩为：

Mpq=E{[X(t)]p-q[X*(t)]q}

(3)

式中，*表示函数的共轭。

定义其各阶累积量为：

C20=Cum(X,X)=M20=E{[X(t)]2}

(4)

C21=Cum(X,X*)=M21=E[X(t)X*(t)]

(5)

C40=Cum(X,X,X,X)=M40-3(M20)2

(6)

C41=Cum(X,X,X,X*)=M41-3M20M21

(7)

C42=Cum(X,X,X*,X*)= M42-|M20|2-2(M21)2

(8)

C60=Cum(X,X,X,X,X,X)= M60-15M20M40+30(M20)3

(9)

C63=Cum(X,X,X,X*,X*,X*)=M63-6M20M41-9M42M21+18(M20)2M21+12(M21)3

(10)

对于接收信号r(t)=s(t)+n(t)，其中s(t)为发送信号，n(t)为零均值的复高斯白噪声，s(t)与n(t)相互独立。由累积量的性质有：

Cum(r(t))=Cum(s(t))+Cum(n(t))

(11)

由式(4)～(10)知，零均值高斯白噪声大于二阶的累积量值为零，则接收信号的累计量可写成：Cum(r(t))=Cum(s(t))。

由此可知，接收信号的高阶累积量等于发送信号的高阶累积量，从而不受高斯白噪声的影响。用式(3)～(10)采用文献[12]的方法计算数字调制信号的高阶累积量。设信号的能量为E，则数字调制信号高阶累积量的理论值如表1所示。

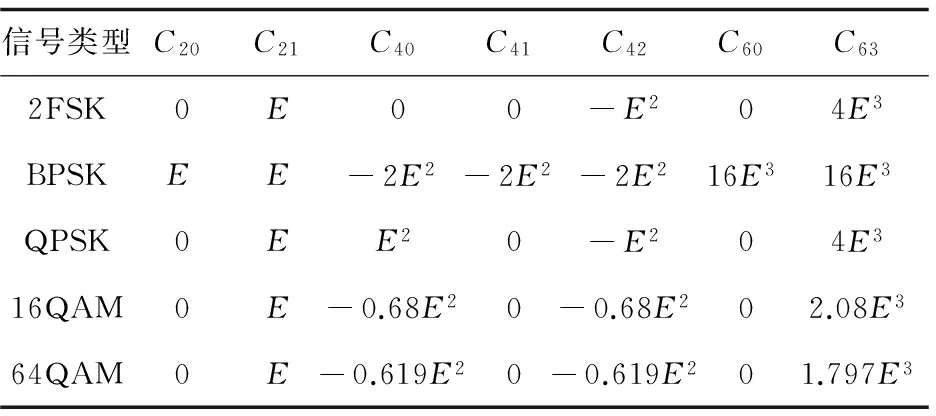
表1 数字调制信号高阶累积量的理论值

因为归一化后能够提高SVM分类精度且能避免噪声和接收信号的功率对识别的影响，文中构建如下归一化特征量：

由上可知，利用F1特征量，可以识别出BPSK；利用F2特征量，可以识别出2FSK；结合F3和F4特征量，可以识别出QPSK、16QAM、64QAM。因此构建特征向量[F1,F2,F3,F4]。

2 改进ABC算法优化的支持向量机分类器

2.1 支持向量机原理

支持向量机(SVM)就是寻找一个最优线性分类平面，即最大间隔超平面。当训练集为非线性时，将其映射到高维线性特征空间，在高维空间中构造最优线性分类超平面[13-15]。

对于文中情况，因为是五种调制信号的识别，设训练样本集为：

(x1,y1),…,(xi,yi),(i=1,2,…,n),x∈Rn,y∈{1,2,3,4,5}

式中，n为样本数量；xi为特征向量；yi为类别标签。

数字信号的调制识别是一种复杂的模式识别问题，不能简单地假设成线性可分，考虑训练集为线性不可分的，优化函数为：

(12)

s.t.,αi≥0,i=1,2,…,n

那么问题的最优决策函数为：

(13)

式中，K(xi,xj)为核函数。

文中采取高斯核函数[16]：

支持向量机分类性能主要依赖于惩罚因子C以及核函数K(xi,xj)参数γ。惩罚因子C越大，对误分类的惩罚越大，核参数影响样本在高维特征空间的分布情况。因此采用人工蜂群算法对惩罚因子以及核参数进行优化能获得较好的识别率。

2.2 传统人工蜂群算法原理

人工蜂群(ABC)算法模拟自然界蜜蜂采蜜的过程，将蜜蜂分为三种不同的工种：采蜜蜂、观察蜂和侦查蜂[17-18]。采蜜蜂和观察蜂的数量各占蜜蜂全体数量的一半。食物源与采蜜蜂数量相等且一一对应。如果某个食物源被采蜜蜂和观察蜂放弃，则该食物源对应的采蜜蜂变为侦查蜂。人工蜂群的搜索活动可概括如下：采蜜蜂根据记忆中的食物源位置在其邻域内确定一个新的食物源；采蜜蜂在回到蜂巢后将它们的食物源信息通过舞蹈与观察蜂共享，观察蜂根据采蜜蜂传回的信息对食物源进行优选；观察蜂根据选择的食物源在其邻域内搜索一个新的食物源；放弃食物源的采蜜蜂变为侦查蜂并开始搜索一个新的随机食物源。

2.3 基于二维均匀设计方法的种群初始化

ABC算法对种群初始构造较为敏感，初始食物源在搜索空间分布不均匀将导致算法的搜索范围受到限制，影响算法的全局搜索能力。用二维均匀设计方法构造初始食物源可以在尽可能少的迭代次数内达到实验要求的精度，从而加速算法的收敛。

在ABC算法中，每个食物源的位置代表优化问题的一个可能解，每个解xi(i=1,2,…,SN)是一个D维向量，D为优化参数的个数，每个食物源的花蜜量对应每个解的适应度。

文中的解向量(C,γ)是二维向量，其中惩罚因子C的搜索范围为[1,100]，核参数γ的搜索范围为[0,0.1]。将C的搜索范围分成均匀五段，分别为[1,20],[20,40],[40,60],[60,80],[80,100]；将γ的搜索范围也分成均匀五段，分别为[0,0.02],[0.02,0.04],[0.04,0.06],[0.06,0.08],[0.08,0.1]。然后，分别以C为横坐标，γ为纵坐标，构建二维平面坐标系，如图1所示。

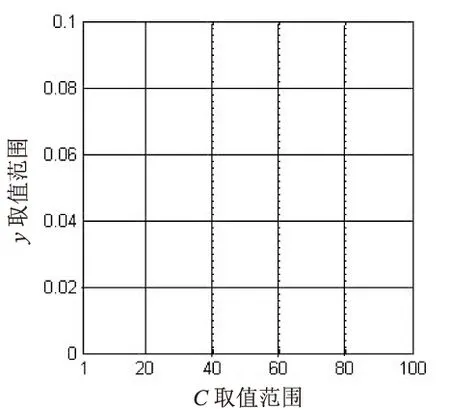
图1 初始食物源的构建范围示意图

图1中每一个方格代表一个解向量的初始构建范围，分别从25个范围中各构建一个解向量作为种群的初始食物源。

2.4 基于欧氏距离的食物源构造方法

在传统的人工蜂群算法中，新食物源的生成公式如下：

vij=xij+φij(xij-xkj)

(15)

式中，k∈{1,2,…,SN}，j∈{1,2,…,D}是随机选择的下标，并满足k≠i；φij为[-1,1]之间的随机数。

由式(15)可以看出，蜜蜂搜寻新解的范围有可能是整个解空间，这使蜜蜂的搜索行为存在盲目性，影响算法寻优效率。

文中提出一种基于欧氏距离的食物源构造方法。在二维平面中，欧氏距离是指两点之间的距离。文中设有食物源(C1,γ1)和(C2,γ2)，定义食物源间的欧氏距离为：

(16)

每一次的迭代过程中，可以得到本次迭代过程中的最优解xbest，那么可以计算出每个解与最优解间的欧氏距离，距离越大，搜索新解的范围就越大，反之，搜索范围越小。

由图1可知，全局最大欧氏距离为两顶点(1,0)和(100,0.1)间距离，定义权重值Δi，如下：

(17)

则食物源的生成公式改进如下：

vij=xij+Δi·φij(xij-xkj)

(18)

2.5 改进人工蜂群算法优化支持向量机参数过程

改进人工蜂群算法优化SVM参数方法描述如下：

步骤一：初始化人工蜂群算法的参数，包括蜜蜂种群的数量、食物源的数量、控制参数limit、最大迭代次数N、SVM参数(C,γ)的范围。

步骤二：将(C,γ)作为ABC算法的解向量，即食物源。根据二维均匀方法在(C,γ)的范围内生成初始食物源(解)，将每个食物源(解)代入SVM计算出识别率，作为适应度。

步骤三：采蜜蜂在每个初始食物源(解)的附近由式(18)生成新的食物源(解)并计算适应度，与初始食物源(解)的适应度进行比较，保留适应度较高的食物源(解)。

步骤五：计算每个食物源(解)的寻优次数是否超过控制参数，若超过控制参数，表示该食物源(解)陷入局部最优，舍弃该食物源(解)，该采蜜蜂变成侦查蜂，由式(18)寻找出新的食物源。

步骤六：若ABC算法达到最大迭代次数，则转至步骤七，否则，转至步骤三。

步骤七：结束ABC训练，输出最优解(C,γ)。

3 仿真结果及分析

为了验证改进ABC算法优化SVM参数能有效地提高调制信号的识别率，在计算机中进行仿真实验。实验平台为MATLAB7.9，安装libsvm工具箱[19]。信号载波频率fc为2 000Hz，采样频率fs为12 000Hz，码元速率fb为500bps，2FSK的频偏为750Hz。信道模型为零均值的高斯白噪声信道。

人工蜂群算法参数具体设置：种群大小为50，食物源大小为25，最大迭代次数为200，控制参数limit为30，惩罚因子C的搜索范围为[1,100]，核参数γ的搜索范围为[0,0.1]，适应度为(C,γ)代入SVM分类器计算出的识别率。SVM训练样本集大小为500，其中各调制信号的特征向量分别为100组，共进行100次蒙特卡洛实验。

3.1 进化曲线对比

图2、图3分别为ABC和改进ABC算法在-3 dB和6 dB时的平均进化曲线。

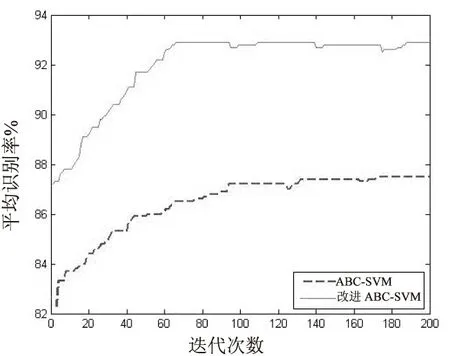
图2 ABC-SVM、改进ABC-SVM在-3 dB下的进化曲线

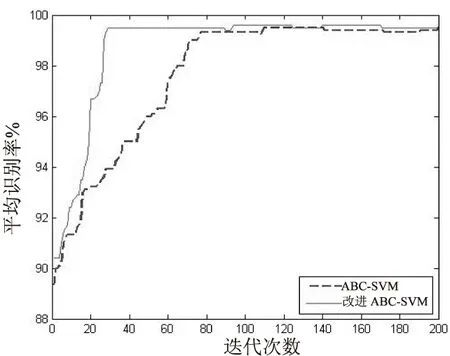
图3 ABC-SVM、改进ABC-SVM在6 dB下的进化曲线

从图中可以看出，改进ABC算法具有更快的全局收敛速度和更好的全局寻优能力。从图2可以看出，改进ABC算法与ABC算法最终收敛的识别率不同，改进ABC算法在93%附近收敛，而传统ABC算法在88%附近收敛，因此在低信噪比的条件下，改进ABC算法有更好的平均识别率。

3.2 识别率对比

图4为ABC-SVM、改进ABC-SVM在各个信噪比条件下的识别率。

从图4可以看出：当信噪比在-3 dB以上时，ABC-SVM算法平均识别率在87%以上，改进ABC-SVM算法识别率在92%以上；当信噪比超过6 dB时，平均识别率均达到99%。由此可见，ABC算法优化的SVM在调制信号的识别中能取得较好的平均识别率，而改进ABC算法在低信噪比下的识别率优于传统ABC算法。在当今日趋复杂的信号环境中，特别在军事对抗中，信号的传输条件非常差。文中提出的改进ABC算法优化支持向量机参数的方法在信噪比较低的情况下有较好的识别率，当信噪比为-3 dB时，平均识别率为92.9%。因此，文中方法在调制识别的现实应用中能取得较为理想的效果。

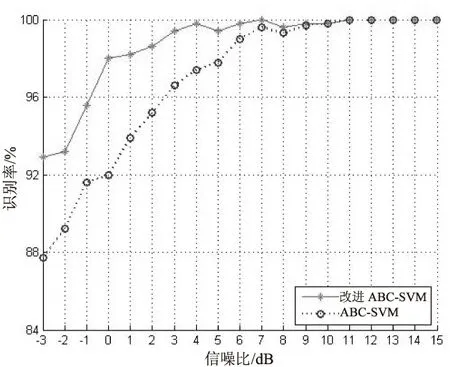
图4 ABC-SVM、改进ABC-SVM在不同信噪比下的平均识别率

4 结束语

文中通过调制信号的高阶累积量构建特征向量，提出采用改进人工蜂群算法优化SVM模型中的惩罚因子和核函数参数的方法，实现了对调制信号的分类识别。针对传统ABC算法中存在的初始种群在解空间分布不均，算法搜索慢和算法收敛慢的缺点，文中提出基于二维均匀设计的初始解构造方法和基于欧氏距离的新食物源构造方法，一定程度上加快了算法的搜索速度和收敛速度。仿真结果表明，人工蜂群算法优化后的SVM模型对调制信号的识别有较高的准确率，在高信噪比的条件下平均识别率接近100%。而改进人工蜂群算法不仅有更好的收敛速度，而且在低信噪比条件下也有近93%的识别率。

人工蜂群算法提出的时间还不长，仍处于起步阶段，对其理论和应用的研究空间还很大，还需要进一步的研究。在后续的工作中，笔者将会对蜂群算法的寻优过程进一步优化，并将其应用于调制信号的识别研究。

[1] Su W,Xu J L,Zhou M C.Real-time modulation classification based on maximum likelihood[J].IEEE Communications Letters,2008,12(11):801-803.

[2] Li Y,Wang F,Zhu G.Hybrid digital modulation classification[C]//Proc of 8th international wireless communications and mobile computing conference.[s.l.]:IEEE,2012.

[3] 王玉娥,张天骐,白 娟,等.基于粒子群支持向量机的通信信号调制识别算法[J].电视技术,2011,35(23):106-110.

[4] Orlic V D,Dukic M L.Automatic modulation classification:sixth-order cumulant features as a solution for real-world challenges[C]//Proc of telecommunications forum.[s.l.]:IEEE,2012:392-399.

[5] Zhang C Q,Zheng J G,Wang X.Overview of research on bee colony algorithms[J].Application Research of Computers,2011,28(9):3201-3204.

[6] 于 明,艾月乔.基于人工蜂群算法的支持向量机参数优化及应用[J].光电子·激光,2012,23(2):374-378.

[7] 刘 路,王太勇.基于人工蜂群算法的支持向量机优化[J].天津大学学报,2011,44(9):803-809.

[8] 臧明相,马 轩,段奕明.一种改进的人工蜂群算法[J].西安电子科技大学学报,2015,42(2):65-70.

[9] 罗 钧,李 研.具有混沌搜索策略的蜂群优化算法[J].控制与决策,2010,25(12):1913-1916.

[10] 毕晓君,王艳娇.改进人工蜂群算法[J].哈尔滨工程大学学报,2012,33(1):117-123.

[11] 张贤达.现代信号处理[M].第2版.北京:清华大学出版社,2002:263-274.

[12] Ho K C,Prokopiw W,Chan Y T.Modulation identification of digital signals by the wavelet transform[J].IEE Proceedings - Radar,Sonar and Navigation,2000,147(4):169-176.

[13] 王建勇,王 海.基于高阶累积量和SVM的OFDM调制制式识别[J].计算机与数字工程,2008,36(6):41-44.

[14] 张学工.关于统计学习理论与支持向量机[J].自动化学报,2000,26(1):32-42.

[15] 孙建成,张太镒,刘海员.基于SVM的多类模拟调制方式识别算法[J].电子科技大学学报,2006,35(2):149-152.

[16] 杜树新,吴铁军.模式识别中的支持向量机方法[J].浙江大学学报：工学版,2003,37(5):521-527.

[17] Karaboga D,Basturk B.A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm[J].Journal of Global Optimization,2007,39(3):459-471.

[18] Karaboga D,Basturk B.On the performance of artificial bee colony (ABC) algorithm[J].Applied Soft Computing,2007,8(1):687-697.

[19] Chang C C,Lin C J.LIBSVM:a library for support vector machines[J].ACM Transactions on Intelligent Systems & Technology,2001,2(3):389-396.

A Modulation Identification Algorithm for Digital Signals Based on Modified Artificial Bee Colony Algorithm

WU Shao-hua,SHAN Jian-feng

(School of Electronic Science and Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210000,China)

In view of the slow convergence speed and non-uniform distribution of the initial food source of traditional Artificial Bee Colony (ABC) algorithm,a modified ABC algorithm based on two-dimensional uniform design and Euclidean-distance has been proposed.Two-dimensional uniform design is used to make the food source uniformly distribute in the solution space when the modified ABC algorithm establishes the food source,which can improve the global search ability of the algorithm.Euclidean-distance is applied in constructing new food source to improve the efficiency optimization.In this paper,four feature parameters which are picked up from second-order,fourth-order and sixth-order cumulants are obtained as a feature vector because second and higher order cumulants can suppress additive white Gaussian noise.SVM classifier and modified ABC algorithm is used to optimize the penalty factor and kernel function parameter,realizing the identification of 2FSK,BPSK,QPSK,16QAM and 64QAM.The simulation results show that the convergence speed of modified ABC algorithm is improved and the average recognition rate is 92.9% when SNR is -3 dB,as well as over 99% when SNR is more than 4 dB.

artificial bee colony;Euclidean-distance;two-dimensional uniform design;support vector machines;modulation identification

2015-09-18

2015-12-22

时间：2016-05-25

国家自然科学基金资助项目(61302155，GZ212015)

吴少华(1990-)，男，硕士生，研究方向为调制信号识别与分类；单剑锋，副教授，博士，研究方向为智能信息处理、调制信号识别、电路故障诊断等。

http://www.cnki.net/kcms/detail/61.1450.TP.20160525.1709.056.html

TP911

A

1673-629X(2016)07-0046-05

10.3969/j.issn.1673-629X.2016.07.010