基于滑模速度控制器的PMSM无速度传感器控制研究*
2016-02-26朱晓虹张广明韩世东孙明山
朱晓虹, 张广明, 梅 磊, 韩世东, 孙明山
(1. 南京工业大学 电气工程与控制科学学院,江苏 南京 211816;
2. 中科院苏州生物医学工程技术研究所,江苏 苏州 215163)
基于滑模速度控制器的PMSM无速度传感器控制研究*
朱晓虹1,2,张广明1,梅磊1,韩世东1,孙明山2
(1. 南京工业大学 电气工程与控制科学学院,江苏 南京211816;
2. 中科院苏州生物医学工程技术研究所,江苏 苏州215163)
摘要:针对传统永磁同步电机(PMSM)矢量控制系统中易受机械式传感器影响的问题,设计了一套基于扩展卡尔曼滤波器(EKF)的PMSM无传感器控制系统;同时由于负载突变和系统参数变化会影响整个控制系统的稳定性,提出一种滑模控制器(SMC)来取代传统PI 速度控制器。首先对PMSM数学模型进行线性化处理,在此基础上引入EKF算法实现转速、位置的在线估计,并且设计以转速误差作为状态变量的滑模速度控制器,实现速度环的闭环调节。仿真结果表明,EKF可以有效地对转子速度、位置进行估算,且在滑模速度控制器的作用下系统响应更快、抗干扰性能更好、鲁棒性更强。
关键词:永磁同步电机; 无传感器控制; 扩展卡尔曼滤波; 滑模控制器
0引言
20世纪80年代以来,随着各方面相关技术的快速发展,交流电机伺服系统应用变得广泛。通常对于小容量的调速系统大多选用永磁同步电机。永磁同步电机转子使用永磁体,省去了励磁绕组、电刷等,因此结构简单、运行可靠[1]。为了实现高精度、高动态性能的伺服控制,一般都采用磁场定向矢量控制或者直接转矩控制。但无论哪种控制方案,都需要转速闭环,因此大部分情况下需要利用同轴安装的速度传感器来测速。但此类传感器抗干扰性差,又在安装场所和价格等方面有所限制,因此无速度传感器技术越来越成为近年的研究热点[2-3]。诸多学者进行深入研究并提出方法。这些方法可以分为以下几类: (1) 直接计算法;(2) 基于观测器的方法;(3) 模型参考自适应控制;(4) 扩展卡尔曼滤波法;(5) 人工智能估算方法。
文献[4]通过直接计算定子电压和电流获得位置角和速度,但该方法依赖于电机的数学模型,需知道电机的参数,因此当电机参数改变时,估算就会有偏差。文献[5-6]是基于滑模观测器的方法,滑模观测器能够很快地跟踪速度,同时鲁棒性也很强,但开关来回切换就不可避免地会产生抖动,学者们在减弱抖动这方面也做了不少工作。哈尔滨工业大学的张晓光等[7]设计了一种负载转矩滑模观测器,将负载转矩作为扩展状态变量,以实际转速和观测转速之差构成滑模面,对负载转矩进行观测,并将观测到的负载作为前馈补偿,能够有效削弱抖振。张洪帅等[8]将模糊控制与滑模观测器结合,实现低速抖振抑制,可以有效地估计电机转子位置,但模糊控制算法训练时间长,系统计算变得复杂。文献[9]提出了一种结合滑模估计器和扩展卡尔曼滤波器(EKF)两种方法优点的混合估计器,参数调节变得容易很多,低速性能也较好。文献[10]对传统EKF算法进行改进,将信息引入到EKF中来修正滤波增益,抑制噪声变化对辨识结果的影响,能够对模型参数准确估计,提高了辨识精度。
目前的一些无速度估计算法基本都能得到较为不错的估计值,但是对于永磁同步电机这个非线性系统来说存在很多不确定因素,例如随机噪声等。鉴于EKF算法对噪声具有非常好的抑制能力,因此本文采用EKF来进行系统状态估计。根据文献[5-6]可知,使用滑模观测器的系统鲁棒性更强,因此本文就利用这点将滑模控制器代替PI控制器,切换函数采用饱和函数替代开关函数以减小抖振,滑模算法实现转速闭环调节,仿真验证,采用EKF方法是合理的,同时系统调速性能也大为提高。
1永磁同步电机在α-β静止坐标系下的EKF模型
在构造EKF时通常可以选择旋转坐标系或静止坐标系。若采用旋转坐标系,卡尔曼程序运算时间较长,不利于实时估计,因此本文使用静止坐标系来构建电机非线性方程。PMSM在α-β两相静止坐标系下的电压方程为
(1)
机械运动方程为
(2)
式中:Uα、Uβ——定子电压在αβ轴的分量;
iα、iβ——定子电流在αβ轴的分量;
ωe、ωr、θe——转子电角速度、机械角速度和转子电角度,其中ωe=Npωr(Np为电机极对数);
Rs、Ls、ψf——定子电阻、定子电感、转子永磁磁链;
Te——电磁转矩;
TL——负载转矩;
B、J——摩擦因数和转动惯量。

(3)
由此完整的电机非线性方程描述如下:
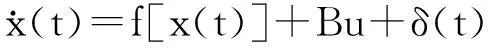
(4)
y(t)=h[x(t)]+μ(t)
(5)
其中:x(t)=[iαiβωrθe]T,u=[uαuβ]T,y=[iαiβ]T。
对f[x(t)]和h[x(t)]进行线性化可以得到Jacobian矩阵:
(6)
(7)
(8)
2扩展卡尔曼滤波器的设计
由于永磁同步电机数学模型是连续的,在估算之前首先应该将电机数学模型离散化。设采样周期为Tc,离散化后电机状态方程为
xk=(1+FTc)xk-1+BTcuk-1+wk-1
(9)
yk=Hkxk+vk
(10)
式中:wk-1——系统噪声;
vk——测量噪声。
他们均值为零且两者互不相关,协方差矩阵分别为Q、R,即Q=cov[w(k)]=E[w(k)w(k)T],R=cov[v(k)]=E[v(k)v(k)T]。
根据EKF递推公式来实现对永磁同步电机电流、转速、位置的估算,具体步骤如下。
(1) 根据k-1时刻的输入值和状态转移矩阵,估计k时刻的状态变量先验估计值:
(11)
(2) 利用状态转移矩阵和k-1时刻估计的误差协方差矩阵计算本次系统误差协方差矩阵Pk/k-1:
Pk/k-1=(1+FTc)Pk-1(1+FTc)T+Q
(12)
(3) 根据预测误差和测量误差计算增益矩阵:
(13)
(4)k时刻状态的最优估计:
(14)
(5) 更新最优估计误差:
Pk=(I-KkHk)Pk/k-1
(15)
EKF算法就是由以上五个步骤递推运算实现的,需要注意的是系统噪声协方差矩阵Q和测量噪声矩阵R的选取将会影响到EKF算法的收敛性,不适当的值可能导致系统发散。本文在前人经验上进行多次试凑与仿真,最终确定了适合本系统的噪声矩阵。
3滑模速度控制器设计
滑模控制在状态空间中为系统设计一个超平面,在不连续的控制规律作用下,迫使系统变换结构,因此滑模控制也叫做滑模变结构控制。其本质就是在控制律的作用下将从任意一点出发的状态轨迹引导到滑模面,如图1所示,从而保证系统在滑模面上稳定运动。因此,滑模控制最重要的是确定控制律和滑模面。

图1 切换面上三种类型运动点
永磁同步电机在dq坐标系下的数学模型:
电磁转矩方程为
(17)
本系统采用id=0的矢量控制方法,如图2所示。式(16)结合式(2)、(17)整理可得:
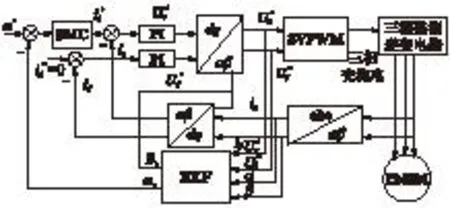
图2 无速度传感器PMSM滑模调速系统
(18)
如图2所示,选择速度差为状态变量e=ω*-ωr(ω*为给定转速),控制量为iq,对转速误差求导可得
(19)
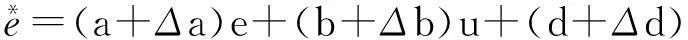
(20)
将式(20)整理可得
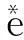
[(E(t)=Δae+Δbu+d+Δd) ]
(21)
由式(19)可以看出永磁同步电机调速模型为一阶微分方程,在设计切换函数时引入了速度误差的积分项,就可以保证系统在整个滑模动态过程中具有鲁棒性。引入积分项的切换函数为
(22)

u=ueq+usw
(23)
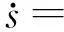
(24)
其中:k表示趋近率,即状态轨迹运动到滑模面的速率;δ表示边界层厚度,系统在δ邻域内不需要进行变结构切换控制,变成一种连续的控制,从而消除了滑模面的抖振现象。
在边界层内,滑模控制器的控制律为
(25)
由上可知s(x)、u+(x)和u-(x)都得到了,因此滑模动态控制系统可以建立,函数切换控制型滑模控制结构如图3所示。

图3 函数切换控制型滑模控制器结构图
为了确定设计的切换函数和控制律是否正确,需要验证滑模的存在性和稳定性。
由式(21)~(23)可得
s[(c+a)e+bu+E(t)]=
s[(c+a)e+b(ueq+usw)+E(t)]=
s[bksat(s,δ)+E(t)]
(26)
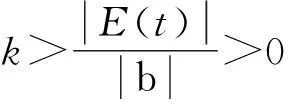
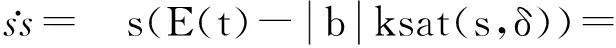
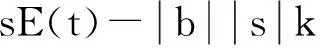

(27)
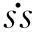
4仿真验证
图4是在给定转速为1000r/min、电机负载为1N起动下电机实际速度和卡尔曼估计的速度。滑模速度控制器的调节加快了进入稳态的时间,估算转速在0.12s后与实际转速曲线重合,几乎没有误差。图5是电机实际转子位置与估算位置,在起动阶段误差稍大,稳定之后两者基本重合,可以看出转角与速度保持了严格的积分关系。
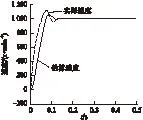
图4 电机实际与估算转速波形
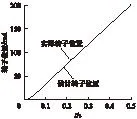
图5 电机实际与估算转子位置波形
图6是转速实际值和估计值之差。起动时速度差最大接近400r/min,这是因为EKF算法是一种递推运行的算法,初始值是随机给定的,所以一开始有估算误差,但随着算法的逐步递推,误差逐渐变小,最终能够完全跟踪实际速度,实现无偏差估计。图7是电机实际角度和估算角度的误差曲线图。由图7可见,稳定后的误差值保持在(-0.15,+0.15)之间,进一步证明EKF的收敛性。

图6 EKF估计转速与实际转速的误差
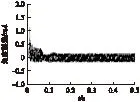
图7 EKF估算位置与实际位置误差波形
图8与图9是给定指令变化时,对应速度响应的变化。图8是在0.25s时将速度指令变成700r/min,可以看到经过0.06s之后,速度再次达到了稳定;图9是在0.25s时突加了5N的负载,一开始速度有所下降,但很快又恢复了给定,是因为滑模控制器的存在才使得系统在系统参数、负载突变时很快恢复原来状态,系统具有很强的鲁棒性。
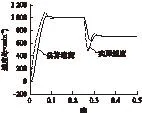
图8 给定指令变化时速度波形
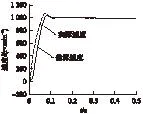
图9 负载转矩变化时速度波形
为了更直观地显示滑模控制器的优越性,图10将滑模控制器与PI控制器进行了对比。首先让电机空载运行,在0.3s时给电机加了8N的负载,由图10可知,PI控制器进入稳定状态需要将近0.1s,而滑模控制器很快能够恢复稳态;图11为永磁同步电机电机控制系统正反转仿真图,转速参考值先是从0加速到1000r/min,0.25s时改变转速给定,使之减速到-1000r/min,从图11中可以看到,PI控制器的动态响应能力不及SMC,再次证明滑模控制器抗干扰性能力强。
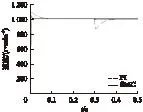
图10 负载变化时SMC与PI对比曲线
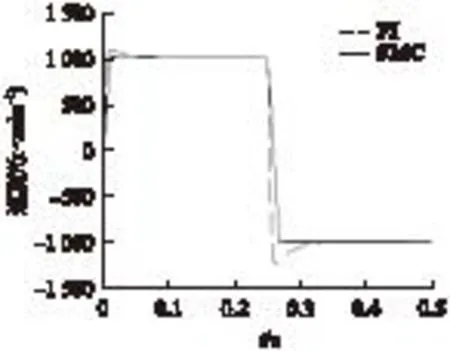
图11 电机正反转SMC与PI对比曲线
5结语
本文设计了一套基于EKF的永磁同步电机滑模调速系统。首先搭建了永磁同步电机数学模型,以此为基础设计以速度误差及其积分之和为滑模面的滑模速度控制器,从而得到q轴电流。EKF的存在简化了系统的硬件结构,虽在起动阶段估算有所误差,但由于滑模速度控制器的存在,加快了系统的动态响应,由此EKF算法经过逐步递推很快能够达到稳定,几乎实现无偏差估计。仿真试验证明该控制方法有抗扰能力强、估计精确等优点。
【参 考 文 献】
[1]陈振,刘向东,靳永强,等.采用扩展卡尔曼滤波磁链观测器的永磁同步电机直接转矩控制[J].中国电机工程学报,2008,28(33): 75-81.
[2]孙旭霞,刘博.基于EKF的PMSM无传感器控制及滤波参数选取[J].微特电机,2011(5): 39-42.
[3]张建军.基于改进的扩展卡尔曼滤波伺服系统建模技术研究[J].计算机应用研究,2012,29(3): 944-946.
[4]SHOUSE K R, TAYLOR D G. Sensorless velocity control of permanent magnet synchronous motors [C]∥Proc of the 33rd IEEE Conference Decision and Control. 2010: 1844-1849.
[5]邱忠才,王斌,郭冀岭,等.卡尔曼滤波滑模变结构PMSM位置速度观测器[J].电力电子技术,2013,47(11): 103-105.
[6]贺宇轩,解小华,张爱春.基于滑模变结构控制的永磁同步电机[J].吉林大学学报: 信息科学版,2015,33(1): 12-18.
[7]张晓光,孙力,赵克.基于负载转矩滑模观测的永磁同步电机滑模控制[J].中国电机工程学报,2012,32(3): 111-116.
[8]张洪帅,王平,韩邦成,等.基于模糊滑模观测器的磁悬浮高速永磁同步电机转子位置检测方法[J].电工技术学报,2014,29(7): 147-153.
[9]刘宇,刘杰,戴丽,等.基于滑模估计器和卡尔曼滤波的PMSM速度估计[J].系统仿真学报,2008,20(1): 162-164.
[10]魏彤,郭蕊.自适应卡尔曼滤波在无刷直流电机系统辨识中的应用[J].光学精密工程,2012(10): 2308-2314.
引领技术发展趋势报道经典实用案例反映行业最新动态
Research on Sensorless Control of PMSM Based on
Sliding Mode Speed Controller
ZHUXiaohong1,2,ZHANGGuangming1,MEILei1,HANShidong1,SUNMingshan2
(1. College of Electrical Engineering and Control Science, Nanjing TECH University, Nanjing 211816,
China; 2. Suzhou Institute of Biomedical Engineering and Technology Chinese Academy of Sciences,
Suzhou 215163, China)
Abstract:A method based on extended kalman filter(EKF)of permanent synchronous motor without position sensor was proposed due to the mechanical sensor problem exiting in traditional PMSM vector control system. At the same time varying load and parameter variations also affect the stability of the whole control system, so a sliding mode controller was used to replace the traditional PI controller. At first, linearizing mathematical model of PMSM,then using extended Kalman filtering algorithm to estimate speed and position, at last, designing speed error as the state variables of the sliding mode speed controller to realize closed-loop control. The simulation results showed that the EKF could estimate the rotor speed and position effectively and system has faster response、better anti-interference performance and stronger robustness under the action of sliding mode speed controller.
Key words:permanent magnet synchronous motors(PMSM); sensorless control; extended kalman filter(EKF); sliding mode controller
收稿日期:2015-07-16
中图分类号:TM 301.2
文献标志码:A
文章编号:1673-6540(2016)01- 0001- 06
作者简介:朱晓虹(1990—),女,硕士研究生,研究方向为电机控制技术。张广明(1965—),男,教授,研究方向为智能控制及其应用、机电系统综合控制、新能源及其控制。
*基金项目:国家自然科学基金(51277092,51307080);国家重大科学仪器设备开发专项项目(2011YQ04008206)
