国际原油价格预测研究
2016-02-26熊熊,李璇
熊 熊,李 璇
(天津大学 管理与经济学部,天津 300000)

引用格式:熊熊,李璇.国际原油价格预测研究[J].重庆理工大学学报(自然科学版),2016(1):48-53.
Citation format:XIONG Xiong, LI Xuan.Prediction of International Crude Oil Price[J].Journal of Chongqing University of Technology(Natural Science),2016(1):48-53.
国际原油价格预测研究
熊熊,李璇
(天津大学 管理与经济学部,天津300000)
摘要:石油是不可再生能源,是经济发展的血液。我国对石油有较大的消费需求,因此油价的波动会导致经济的波动。原油价格波动较为复杂,不确定性影响因素较多。ARIMA模型广泛地应用在高频金融时间序列建模,能较好地把握此类时间序列的动态规律。从计量经济学的角度运用EVIEWS软件,对1996—2013年的国际原油价格进行数据整理归纳,运用ARIMA模型加入季节因子建立原油价格模型,并通过模型走势对2014—2020年的国际原油价格进行预测。
关键词:ARIMA;石油价格;预测
原油作为最基础的能源和化工原料,被誉为“现代工业的血液”、“运输工具的粮食”,在国民经济的发展、民生状况的改善中起着举足轻重的作用。根据BP世界能源统计(2010),在75个国家中,有45个国家原油在能源消费中占据第一位。在世界能源消费构成中,原油也已超越煤炭,成为全球第一大能源(占比超过1/3)。原油价格的波动影响着世界经济的脉搏,对世界各国的能源战略和能源安全也影响重大,因此研究原油价格的走势具有重要意义。
本文试从计量经济学的角度,运用EVIEWS软件,对1996—2013年的国际原油价格进行数据整理,运用ARIMA模型[4-9]并加入季节因子建立原油价格模型,并通过模型走势对2014—2020年的国际原油价格进行预测。
1ARIMA模型
1.1数据来源
本文选取1996—2013年的原油月度价格,具体是以1996年1月—2013年11月的国际原油月均价格(库欣原油现货离岸价格)作为本文的数据来源。数据来自于互联网公布的库欣原油现货离岸价格日成交价,并手工整理出月平均价格。本文将石油月均价格时间序列定义为X1。
1.2模型建立
1.2.1序列平稳性检验
现实中的真实数据通常没有统计假设的完美,时间序列的数据常常出现不平稳的状况。因此,在进行具体建模之前,需要运用统计方法检验时间序列的平稳性,这里采用单位根检验法。单位根检验主要对序列的方差进行分析,进而分析序列的变动趋势,以及所具有的季节特征。计算结果见图1、2。

图1 序列平稳性测试
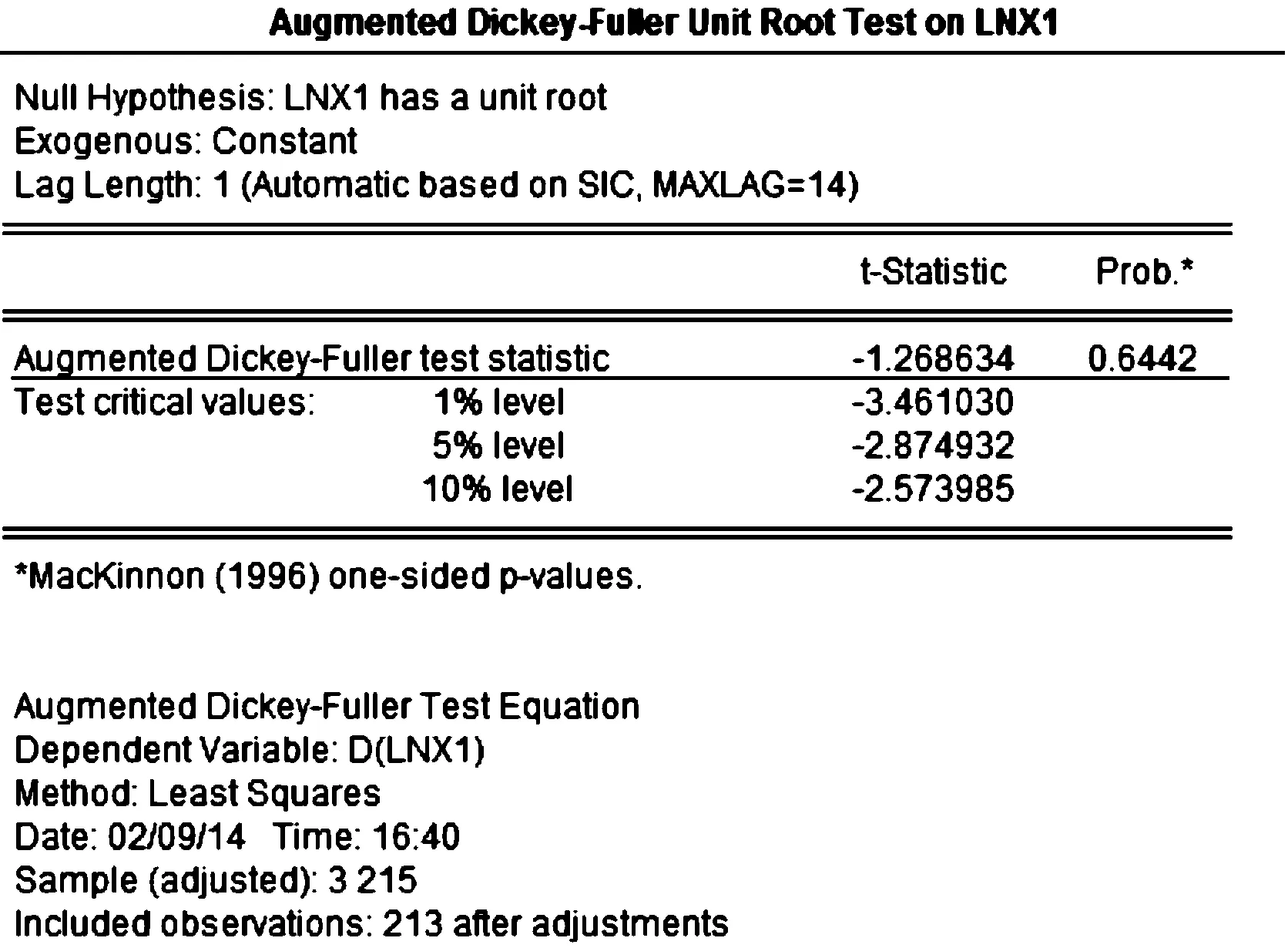
图2 序列取对数后的平稳性测试
图1显示:原序列存在单位根,序列不平稳,需要进行平稳化处理。因此,对原序列取对数,判断对数运算后的序列是否平稳进行测试。如图2所示,原序列经取对数运算后,仍然不能拒绝原假设,对数后的序列仍存在单位根,需要对序列进行平稳化。
2.节水工程的制约。由于渠道衬砌及管灌等节水工程实施,原有渠道进行了衬砌,没有为农田林网建设预留林业用地,要栽植农田林网必需占用少量耕地,导致林农矛盾突出;同时渠道衬砌后灌溉林木用水明显减少,不能按时完成林网灌溉,限制了农田林网建设。
1.2.2序列平稳化处理
序列平稳化的常用方法是进行差分处理。通过相关处理技术和多次差分处理,差分方法能有效改善数据中存在的异方差。处理后的数据结果不仅单位根检验达标,自相关图和偏相关图也达到统计运算需要达到的平稳性。计算结果见图3、4。

图3 对序列取一阶差分的单位根检验
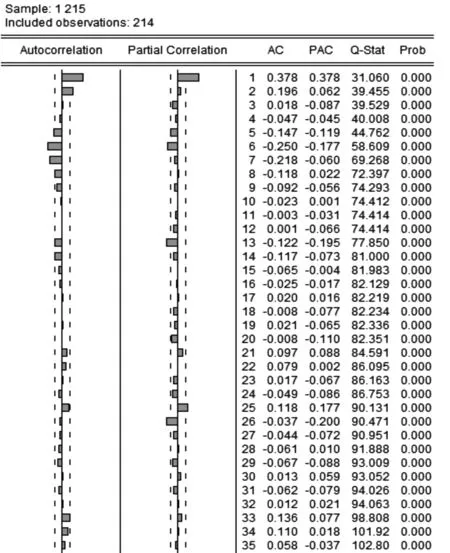
图4 对序列取一阶差分的自相关和偏相关检验
如图3所示,对于原序列取一阶差分,通过结果应拒绝原假设,一阶差分后的原序列不存在单位根。如图4所示,通过一阶差分后的自相关图和偏相关图可以看到:一阶差分后的序列基本实现平稳,但不够优化。由于对原序列直接取一阶差分结果不够理想,因此再针对lnX1做一阶差分,结果见图5、6。
由图5可见:一阶差分后的lnX1不存在单位根,数据较为平稳。图6用自相关图和偏自相关图检验序列的平稳情况。通过对原序列直接取一阶差分和原序列先取对数再取一阶差分可以看到:原序列先取对数再取一阶差分的结果更好,数据更平稳。因此,选择d(lnX1)作为建模序列。
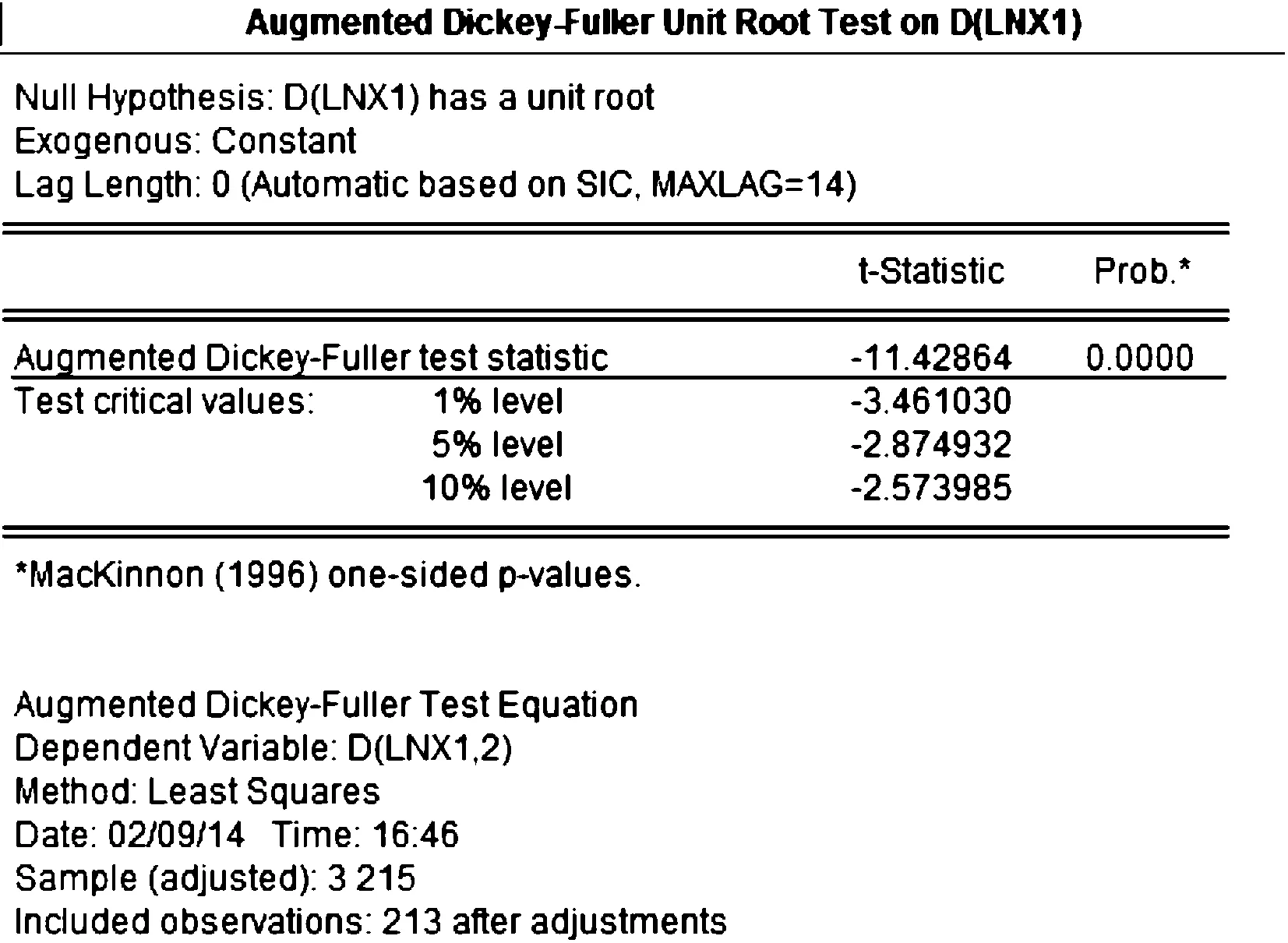
图5 对LnX1取一阶差分的单位根检验
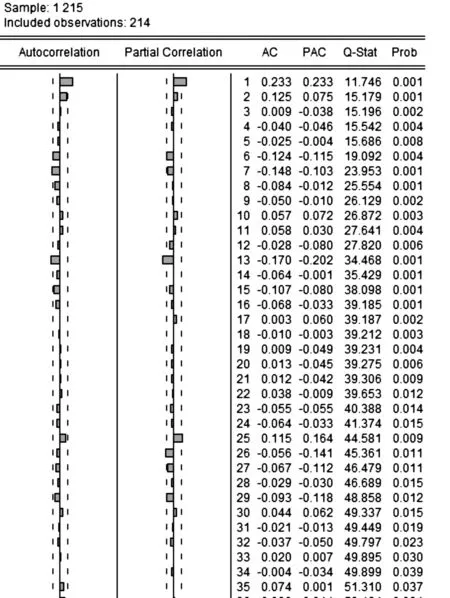
图6 对LnX1取一阶差分的自相关和偏相关检验
1.2.3模型参数的确定
根据自相关和偏相关图的尾部特征不同,ARIMA模型又可具体分为AR模型、MA模型以及ARMA模型,其中自相关和偏相关图如果具有双拖尾特征,适合采用ARMA模型,如果自相关和偏相关图还体现了明显的季节性变化特征,则还需运用SARMA模型。
通过图6可以看到:d(lnX1)序列偏相关函数和自相关函数具有明显的双拖尾特征,适合采用ARMA模型[10-13]。又由于序列在第1、13、25期均出现了浮动,可见该序列还存在季节性,因而进一步引入SAR变量,模型为SARMA模型。建模结果见图7。

图7 序列建模结果
通过图7可以看到:各参数均处于置信区间之中,具有很高的可信性。建模之后的可决系数和调整后的可决系数很高,证明模型对序列的拟合程度非常好。F检测的概率为0.00,拒绝原假设,建立模型成立。综上所述,该模型具有统计意义。
1.2.4模型确定
根据上面系数的确定,建立模型方程如下:
D(LOG(X1),1,12)=C(1)+
[AR(1)=C(2),AR(2)=C(3),
SAR(12)=C(4),MA(1)=C(5),
MA(2)=C(6),SMA(12)=C(7),
BACKCAST=28,ESTSMPL="28215"]
Substituted Coefficients:
D(LOG(X1),1,12)=-0.001 044 636 705 63+
[AR(1)=1.381 906 047 95,
AR(2)=-0.887 815 989 593,
SAR(12)=-0.147 796 906 879,
MA(1)=-1.334 233 018 96,
MA(2)=0.939 282 153 312,
SMA(12)=-0.960 495 252 05,
BACKCAST=28,ESTSMPL="28215"]
1.3模型检验
1.3.1模型的统计学检验
从检验结果可以看到:各参数的概率都小于0.05,T检验的绝对值都大于2,统计检验结果良好。
1.3.2模型的白噪声检验
通过图8对模型残差的自相关检验可以看到:残差满足白噪声序列,模型建立良好。
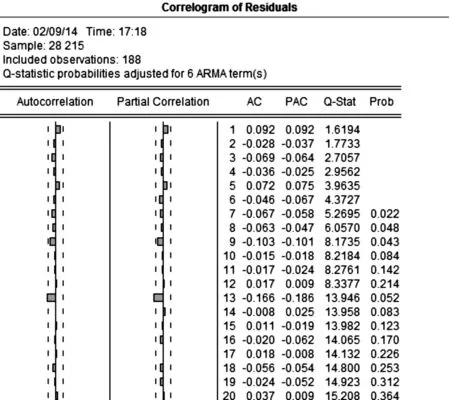
图8 模型的白噪声检验
1.3.3模型的样本内预测检验
直观图比较法是一种简单易操作的度量模型可依赖性的方法。该方法虽然在统计意义上并不精确,但可以判断模型总体上的准确程度。通过图9可以直观看到:模型的拟合情况较好。
差额百分比是数学统计上一种重要的模型检验方法,通过比较模型预测结果和实际数据可以有效判断模型的准确程度和精确程度。如图10所示,通过差额百分比可以看到:预测值和实际值的差额占实际值基本控制在0~0.2之间,拟合情况良好。
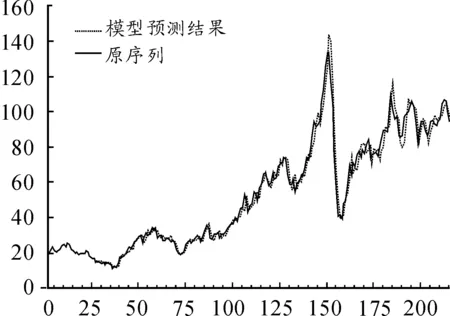
图9 序列与预测结果直观比较
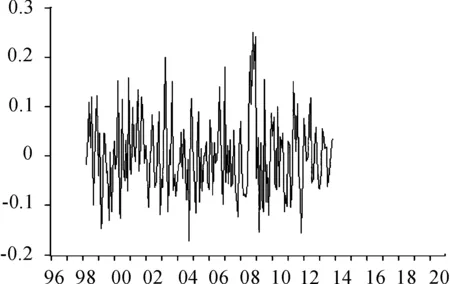
图10 模型的差额百分比
通过对模型进行统计学检验、白噪声检验、直观图检验和差额百分比检验,可以看到:前文建立的ARIMA模型对石油价格预测的精确度较高,模型较为精确,对原油价格的分析和预测具有一定的参考意义。
2石油价格走势分析及建议
国际原油的价格预估及相关分析领域一直倍受大量学者和企业的关注,而油价随市场需求和经济形势的不断变化,既具有线性关系,又具有非线性特征。本文利用ARIMA模型捕捉石油价格中的线性趋势,对WTI原油价格的实证研究表明:本文使用的油价预测模型长期来看是有效的,能够较为准确地预测原油价格的变化趋势,从而达到对世界油价进行预测的目的。同时,在一定程度上验证了组合模型比单一模型具有更高的合理性和准确性。该预测模型是一种有效的石油价格时间序列预测模型。
建立原油价格统计模型主要是为了进行价格分析和预测,根据上述定量预测的结果(如图11所示),从中、短期来看,由于石油市场的供求关系不平衡、石油主要产出国的石油产量控制、各国石油需求增长(特别是新兴国家的需求)、国际金融投机等一系列导致油价上涨的因素作用,使得油价仍会在高位保持一段时间。预计在2014—2015年原油价格仍有上升,将在出现一个小高峰之后振荡下滑。在2020年,预计原油价格将回归至70美元/桶的价位。
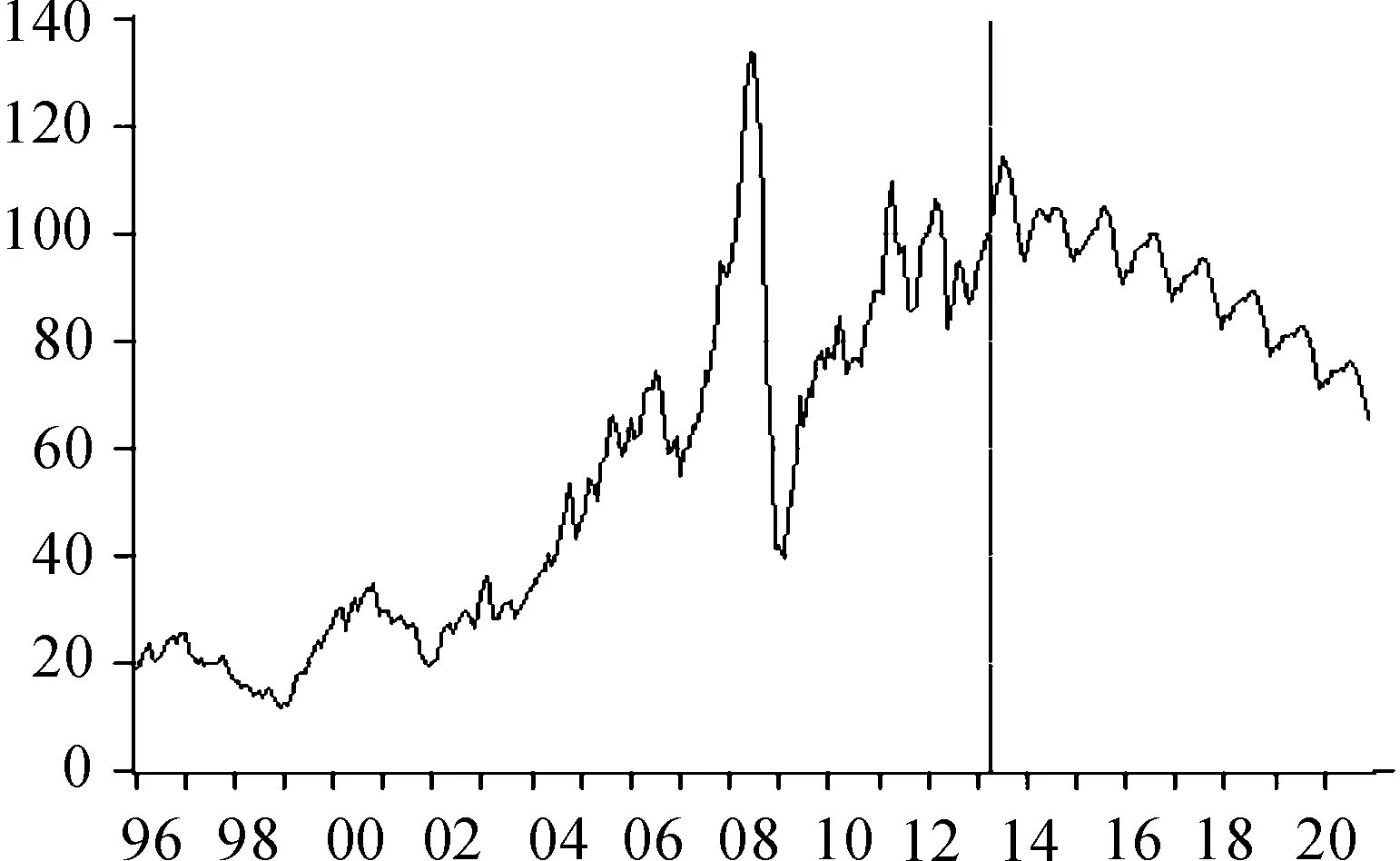
图11 原油价格预测走势
同时应注意到,政局的变动和政策变化会对石油价格产生人为的并不规律的影响。例如,在2000年3月,国际原油输出国组织的成员国达成了一项协议,决定从4月1日起每日增产原油170万桶。这一增产的决定导致了油价的大幅下降。又如在2001年,由于”911“事件后人们对于全球经济的预期并不乐观,从10月份开始,油价急剧下挫。由此可见,全球经济形势、政治局势、突发事件等作为关键因素对油价波动的影响是较为明显的。因此,企业在进行油价预测以及做出相关决策的过程中,在进行定量预测时,要注意结合相关影响因素进行全面分析,同时密切关注国际上发生的重大政治、军事和经济事件,才能得出更加准确的石油价格预测结果,从而做出正确的经营决策。
由于世界经济的快速发展,国际政经形势的不断变化,影响油价的因素极为复杂,多年的油价数据也没有体现出准确的规律。本文利用ARIMA模型的特点,即以数据序列的已有数据预测未来数据的特点,以大量的油价历史数据为依据,最大程度地降低了不受控因素(如政局变动、突发事件等)对预测结果的影响。经过多次的参数修改,加上反复用历史油价进行模型的验证,最终得到了较为准确的预测模型,从而达到了较为准确地预测短期油价的目的。由于影响油价的因素非常复杂,本文仅考虑了历史数据,预测的油价需要结合当前的世界政经形势进行调整,同时由于数据量有限,此预测结果可能存在一定的误差。随着时间的推移,新的实际油价数据不断更新,需要对模型的相关参数进行调整或重新拟合,以提高预测精度。
参考文献:
[1]吴敬婷.农产品价格时间序列几种预测模型的研究[J].黑龙江科技信息,2013(31):93-95.
[2]丁静之,闵骐,林怡.ARIMA模型在石油价格预测中的应用[J].物流技术,2008(10):156-159.
[3]刘爱萍,郜文明.ARIMA模型在省级全社会固定资产投资预测中的应用[J].河南金融管理干部学院学报,2008(4):105-107.
[4]侯璐.基于ARIMA模型的石油价格短期分析预测[D].广州:暨南大学,2009.
[5]吴虹,尹华.ARIMA与SVM组合模型的石油价格预测[J].计算机仿真,2010(5):264-266.
[6]徐建英,何旭宏.数据统计分析与spss应用[M].北京:人民邮电出版社,2003.
[7]赵银飞.基于SAS的港口统计决策支持系统研究与设计[D].北京:北京交通大学,2010.
[8]易丹辉.数据分析与EVIEWS的应用[M].北京:中国统计出版社,2002.
[9]陈夫凯,夏乐天.运用ARIMA模型的我国城镇化水平预测[J].重庆理工大学学报(自然科学版),2014,28(4):133-137.
[10]邹柏贤,刘强.基于ARMA模型的网络流量预测[J].计算机研究与发展,2002(12):1645-1652.
[11]韩瑞玲,佟连军,朱绍华,等.基于ARMA模型的沈阳经济区经济与环境协调发展研究[J].地理科学,2014(1):32-39.
[12]张勃,刘秀丽.基于ARIMA模型的生态足迹动态模拟和预测[J].生态学报,2011,31(20):6251-6260.
[13]李瑞莹,康锐.基于ARMA模型的故障率预测方法研究[J].系统工程与电子技术,2008(8):1588-1591.
(责任编辑陈艳)
Prediction of International Crude Oil Price
XIONG Xiong, LI Xuan
(College of Management and Economics, Tianjin University,Tianjin 300000,China)
Abstract:Oil is a non-renewable energy sources, and it is the blood of economic development. China is a major oil importer and consumer, so oil price fluctuations have a great impact on the operation of the price system and the economy of China. Oil price fluctuations is complex, depending on different uncertain factors. ARIMA model is a random sequence and is widely used in high frequency financial time series. It can grasp the laws of dynamic time series. This paper tried to analyze oil price(1996-2013) by using ARIMA model to establish a price model with seasonal factor in the econometrics perspective. Also, this paper used this model to predict oil price from 2014 to 2020.
Key words:ARIMA; oil price; prediction
文章编号:1674-8425(2016)01-0048-06
中图分类号:TK-9;O21
文献标识码:A
doi:10.3969/j.issn.1674-8425(z).2016.01.009
作者简介:熊熊(1972—),男,湖南常德人,博士,教授,博士生导师,主要从事金融数学研究;李璇,硕士,主要从事并购、资产评估方面研究。
基金项目:国家自然科学基金资助项目(71271145);教育部博士点基金资助项目(20110032110031)
收稿日期:2015-02-25
