一种结合模拟退火和贪心策略的社团识别算法

王丰雪,陈家琪

(上海理工大学 光电信息与计算机工程学院,上海　200093)



一种结合模拟退火和贪心策略的社团识别算法

王丰雪,陈家琪

(上海理工大学 光电信息与计算机工程学院,上海200093)

摘要为了提高复杂网络社团识别的精度和速度,文中结合模拟退火和贪心策略识别社团结构的优势,提出一种新的社团识别算法。该算法利用贪心策略引导模拟退火搜索最优解过程中单个结点的无规则盲目移动,消除了大量无效移动,在搜索到全局最优解的情况下,将搜索时间大幅缩减。实验表明,SAGA具有强大的搜索能力和较快的模拟退火执行速度,可获得较高的模块度,达到较为准确的社团分割,且具有一定的应用价值。

关键词复杂网络;社团识别;SAGA算法;模拟退火;贪心策略

现实世界中的许多系统以网络的形式存在,且具有较高的复杂性,如社交网、 生物信息网和万维网等,因此复杂网络的研究具有重要的理论价值和实际意义。研究表明,复杂网络具有明显的社团结构,即网络中的结点连接情况宏观上可划分为各个集合,集合内的结点间的连接很稠密,而集合与集合之间的结点连接很稀疏[1-2]。复杂网络的社团结构与网络的功能有着紧密的联系,网络社团结构的检测有助于理解网络的拓扑结构和动力学行为,因此找出网络的正确社团结构并分析相关性质具有重要意义[3-5]。

目前复杂网络社团识别算法方面的研究较多,主要分为两类:一类是分离法,即找出社团之间的边,将其从社团中移除;另一类是聚合法,将联系紧密的点聚合为一个社团,通过优化某个社团划分质量指标实现聚合。第一类算法的典型代表是GN分裂算法[6],该算法是复杂网络社团识别研究领域的一种标准算法[7],但时间复杂度较高。第二类算法的典型代表是Louvain算法[8]、模拟退火网络社团识别算法[9]和极值优化模块度识别法[10]等。

Louvain算法是基于贪心策略实现的,划分速度相当快,但不保证划分结果的准确度。模拟退火算法能获得全局最优的模块度值,达到较准确的社团划分,但划分速度相当慢。基于Louvain算法和模拟退火算法这种优缺点互补关系,本文对贪心策略结合模拟退火识别网络社团进行研究,提出一种新的社团识别算法SAGA(Simulated Annealing And Greedy)。该算法用贪心策略消除模拟退火算法中结点移动运动的盲目无规则性,使结点的每次均向模块度增大的方向移动,缩短模拟退火算法获取最优值的时间。

1相关概念

1.1模块度

模块度Q是最常用的衡量社团划分质量的标准,模块度Q越大,表明社团划分算法的划分效果越好,划分结果越符合网络的客观实际社团结构。模块度Q的计算公式如下

(1)

其中,NM是社团数;L是网络中的边数;ls是社团s内的结点之间的边数,ds是社团s内结点的度数之和。

1.2模拟退火

模拟退火算法应用复杂网络社团识别时,将温度T当作控制参数,模块度函数Q取反当作内能E。识别过程[11]:首先,在初始温度下,将每个网络结点初始化为一个独立的社团,计算出这一初始网络社团划分状态下的内能。然后,逐渐降低温度,每一温度T下,执行N2次结点从一个社团随机地移动到其他社团的运动和N次两个社团合并运动或一个社团分裂为二个社团的运动,从而获得新划分状态,计算新状态的内能,用Metropolis准则决定是否接受生成的新状态,直至E趋于全局最小值。内能E最小时对应的社团划分结果即为网络的最优社团划分。Metropolis接受准则的数学公式如下[12]

(2)

其中,Ei是当前状态的内能;Ej是生成的新状态的内能;k为Boltzmann常数。

模拟退火识别网络社团统计上能保证找到全局最优值,缺点是搜索过程耗时过长。

1.3贪心策略

贪心策略是指在对问题求解时总是做出在当前看来是最佳的选择,即不从整体最优上加以考虑,只做出某种意义上的局部最优选择。文献[8]提出的Louvain社团识别法就基于贪心策略优化模块度来获取网络社团结构的。Louvain算法划分速度相当快,但不保证划分全局最优性。

2SAGA算法

2.1算法思想

导致模拟退火识别网络社团收敛速度相当慢的原因:降温过程的每一温度下会执行N2次某一单个结点从一个社团随机地移动到其他社团的运动,N为网络中的结点数。这每一温度下的N2次结点的运动是随机的,无方向性的,无引导的,必定包含很多未能使网络社团划分状态对应的目标函数值更优的结点运动。

针对这一问题,本文用贪心策略指导这每一温度下的N2次的结点运动,除去这一运动过程的盲目性,即除去了很多于收敛到最优模块度值无用的结点移动,使每个结点的每次移动都向模块度值增加的方向移动,使搜索过程更快地收敛到最优模块度值。具体策略是:对某个结点i的移动运动,首先计算其从所属的社团移入邻居节点j所属的社团的模块度增量,计算公式如下

ΔQ=ΔQout+ΔQin

(3)

其中,ΔQout为结点i从其所属的社团移出时产生的模块度增量,ΔQin为结点i移入其的邻居节点时所属的社团时产生的模块度增量。ΔQout和ΔQin的表达式相似,将一个孤立结点放入一个社团C时所产生的模块度增量计算公式如下

(4)

其中,∑in表示社团C内边的权值之和;∑tot表示连接到社团C内的结点的边的权值之和;Ki表示连接到结点i的边的权值之和;Ki,in表示连接结点i和社团C内的结点的边之和;m为网络内所有边的权值之和。之后,将结点i放入使模块度增量最大且模块度值为正数的社团中,若不存在这样的模块度值,则结点i继续保留在其原来所在社团中。对每一温度下要移动的N2个结点执行此操作,N为网络中的结点数。

2.2算法执行流程

为便于更好地理解基于模拟退火和贪心策略的SAGA算法,在此给出SAGA网络社团识别算法的整体流程图。SAGA识别网络社团流程如图1所示。

图1　SAGA社团划分法流程图

3实验和分析

该实验数据来自文献[13]中提到的标准数据集海豚社群Dolphin网络,文献[14]中提到的空手道俱乐部Karate网络,以及从Newman个人网站[15]下载的标准数据集美国政治书Polbooks网络。这3个数据集的相关详细信息如表1所示。

表1　实验数据集

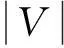
3.1实验环境

硬件配置:IntelCorei5-3470CPU@ 3.20GHz,2.00GB内存。

软件环境:Windows7旗舰版操作系统,Matlab2012b的编译环境。

3.2实验结果和性能评价

3.2.1SAGA算法识别速度评价

本文提出的SAGA社团识别算法是在模拟退火(SimulatedAnnealing,SA)社团识别算法上改进的,目的是在不改变SA较高识别准确度的条件下,大幅度缩短SA快速的识别时间。因此,实验设定SAGA和SA两个算法搜索到相同的最优模块度Q值的情况下,比较两个算法所花费的时间,计算SAGA与SA所花费的时间的百分比tSAGA/tSA。将SAGA和SA应用在3个网络数据集Karate、Dolphin和Polbooks上进行社团划分,实验结果如表2。

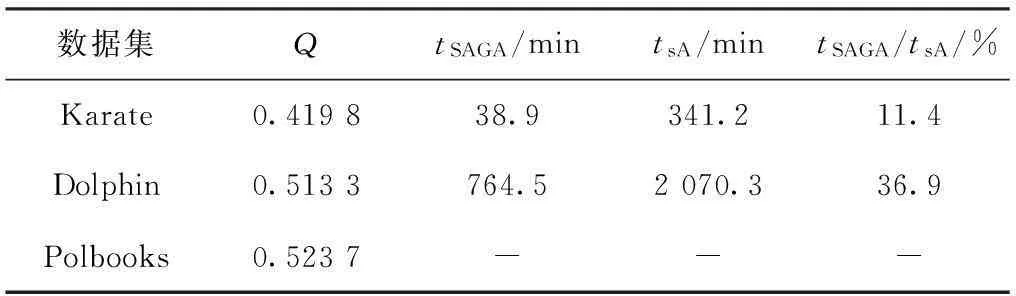
表2　识别时间比较

注:-表示计算时间超过了24 h。

表2所示,在获取到相同的模块度Q的条件下,Karate数据集上SAGA所需时间是SA所需时间的11.4%,Dolphin数据集上SAGA所需时间是SA所需时间的36.9%,表明由模拟退火和贪心策略结合的SAGA算法可大幅缩短SA获取最优值的时间,具有快速的识别速度。另外,在网络的结点规模超过100个结点时,SAGA算法和SA算法在本文的实验条件和实现方式下,其所需时间均超过24 h,表明SAGA算法和SA算法均只适合于规模较小的网络社团划分。

3.2.2SAGA算法识别精度评价

社团识别算法的识别精度主要依据算法运行后所获得的模块度Q值来确定,Q值越大表明算法的识别精度越高,Q值由式(1)计算而得。SAGA算法是在贪心策略社团识别上做的改进研究,目的是获得比贪心策略社团识别法(Greedy算法)和Louvain社团识别法更优的结果。因此,将SAGA算法、Greedy算法、Louvain算法应用在Karate、Dolphin、Polbooks这3个标准网络数据集上进行社团划分实验,3个算法所获模块度Q如表3所示。

表3　模块度Q比较

表3所示,在Karate、Dolphin、Polbooks数据集上,SAGA所获的模块度Q均大于Greedy算法、Louvain算法所获的模块度。表明SAGA算法确实拥有比较高的识别精度,能够达到比较准确的社团划分。同时,也表明由模拟退火和贪心策略结合的SAGA算法能有效地避免贪心策略易陷入局部最优的问题。

4结束语

本文对模拟退火和贪心策略进行结合研究,提出一新的社团识别算法SAGA。实验结果表明SAGA具有强大的搜索能力和较模拟退火快速的执行速度,在精度要求较高且时间要求较快的场合具有一定的应用价值。另外,SAGA算法识别速度与精度受执行贪心策略的结点运动数影响。如何找到一个普适准则来计算此结点数,使SAGA在任何网络下都具有最优识别性能,这有待于进一步研究。

参考文献

[1]Guimera R,Danon L,Diaz-Guilera A,et al.Self-similar community structure in anetwork of human interactions[J].Physical Review E,2003,68(6):065103-065108.

[2]Hartwel L L H,Hopfield J J,Leibler S,et al.Frommolecular to modular biology[J].Nature,1999(402):C47-C52.

[3]Dorogovtsev S N,Mendes J F F.Evolution of networks:from biological nets to the internet and www[M].UK:Oxford University Press,2003.

[4]Girvan M,Newman M E J.Community structure in social and biological networks[J].Proceedings of the National Academy of Sciences of the United States of America,2002,99(12):7821-7826.

[5]Newman M E J.Detecting community structure in networks[J].The EuropeanPhysical Journal B-Condensed Matter and Complex Systems,2004,38(2):321-330.

[6]Danon L,Diaz-Guilera A,Duch J,et al.Comparing community structure identification[J].Journal of Statistical Mechanics-Theory and Experiment,2005(9):09008-09016.

[7]Arenas A,Danon L,Diaz-Guilera A,et al.Community analysis in social networks[J].The European Physical Journal B-Condensed Matter and Complex Systems,2004,38(2):373-380.

[8]Blondel V D,Guillaume J L,Lambiotte R,et al.Fast unfolding of communities in large networks[J].Journal of Statistical Mechanics-Theory and Experiment,2008(6):10008-10017.

[9]Guimera R,Amaral L A N.Functional cartography of complex metabolic networks[J].Nature,2005,433(7028):895-900.

[10]Boettcher S,Percus A G.Optimization with extremal dynamics[J].Complexity,2002,8(2):57-62.

[11]Metropolis N,Rosenbluth A W,Rosenbluth M N,et al.Equations of state calculations by fast computingmachines[J].Journal of Chemical Physics,1953(21):1087-1092.

[12]Kirkpatrick S,Gelatt C D J,Vecchi M P.Optimization by simulated annealing[J].Science,1983,220(4598):671-680.

[13]Lusseau D,Schneider K,Boisseau O J,et al.The bottlenose dolphin community of doubtful sound features a large proportion of long-lasting associations[J].Behavioral Ecology and Sociobiology,2003,54(4):396-405.

[14]Zachary W W.An information flow model for conflict and fission in small groups[J].Journal of Anthropological Research,1977,33(4):452-473.

[15]Newman Mark.Network data[EB/OL].(2014-12-28)[2015-01-09]http://www-personal.umich.edu/～mejn/netdata/.

A Community Detection Combining Simulated Annealing and Greedy Method

WANG Fengxue,CHEN Jiaqi

(School of Optical-Electrical and Computer Engineering,University of Shanghai for

Science and Technology,Shanghai 20093,China)

AbstractTo promote the accuracy and velocity of detection for the community structure in the network,this paper proposes the new community detection method of simulated annealing and greedy algorithm (SAGA),which combines the simulated annealing algorithm and greedy optimization.This algorithm uses greedy strategy to guide the irregular and blind movement of many single nodes in searching the optimal solution of the simulated annealing algorithm,thus removing many invalid movements and greatly reducing the search time to achieve the global optimal solution.The results show that SAGA has higher execution speed with better search ability to obtain higher modularity than the simulated annealing algorithm,and can be effectively used in certain applications.

Keywordscomplex network;community detection;modularity;simulated annealing;greedy optimization

中图分类号TP393.02

文献标识码A

文章编号1007-7820(2016)02-008-04

doi:10.16180/j.cnki.issn1007-7820.2016.02.003

作者简介:王丰雪(1991—),女,硕士研究生。研究方向:复杂网络社团识别。陈家琪(1957—),男,教授。研究方向:计算机网络与信息安全等。

基金项目:上海市教委科研创新基金资助项目(12zz146)

收稿日期:2015- 07- 06