自锁底纸箱底部结构角度尺寸计算分析
2016-02-25李剑华黄昌海
李剑华 黄昌海
所谓自锁底纸箱,是指客户在使用过程中只需张开原本叠平的箱体,就能使其恢复到正常纸箱形状,底部自动连成箱底结构并牢牢锁住的纸箱。整个成箱过程不需要额外组装或底部封箱,可极大减少成箱装配时间。而且,自锁底纸箱也满足现代自动化包装设备的生产需求,在网购盛行的当下,在发货量大、时间紧迫的情况下,自锁底纸箱成为了各大电商的最佳选择,并逐渐得以广泛使用。能够实现如此方便的成箱方式,关键在于自锁底纸箱底部结构合理的角度尺寸设计,下面笔者将对此进行详细介绍,期望能给业内人士起到一定指导作用。
底部结构设计中存在的问题
近来,笔者发现接触到的大部分自锁底纸箱在设计中都存在一个现象,即自锁底纸箱成型时会出现强行压挤纸箱箱体,造成纸箱箱体出现多余压线的现象。这不仅会影响纸箱的整体外观,而且会造成纸箱空箱抗压强度的衰减。
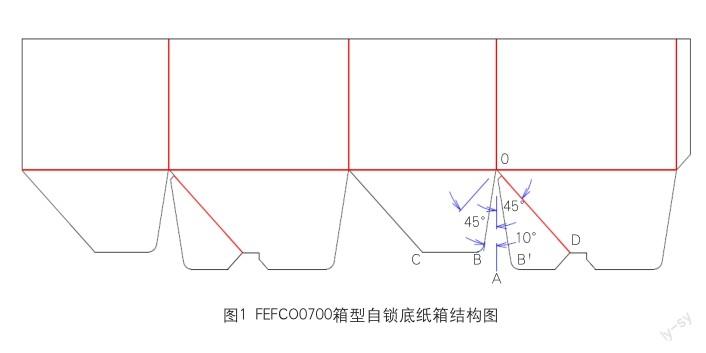
图1为FEFCO0700箱型自锁底纸箱结构图。纸箱底部结构处有几个角度值,其中∠AOC和∠AOD为45°,∠AOB和∠AOB为10°,其中∠AOB和∠AOB的角度值是常见的自锁底纸箱底部结构设计角度。结构图可以通过软件模拟出箱底部结构折叠成型的主要步骤,如图2~图5所示。
依据图1可以发现,尤其在图4与图5中的红蓝线所框部分,三角形红色线框部分已超出纸箱的箱体,形成了不应出现的纸板干涉现象。这种情况的出现表示自锁底纸箱在成型过程中纸板会伸出纸箱箱体外侧,而反应在实际情况中则是红色三角形线框部分会直接挤压箱体内部。
底部结构角度尺寸计算分析
通过上述分析可以看出,自锁底纸箱底部结构角度尺寸的设计应该更加严谨,以避免纸板干涉及纸板挤压箱体。下面,笔者从几何数学的角度来论证合理可行的自锁底纸箱底部结构角度尺寸。
使用软件模拟自锁底纸箱的折叠过程,而非实际产品折叠,因为实际折叠中发生的干涉部分,在软件模拟折叠过程中,纸板不会发生干涉弯曲,而是自然伸展状态。所以,利用软件模拟只能用以研究推算。
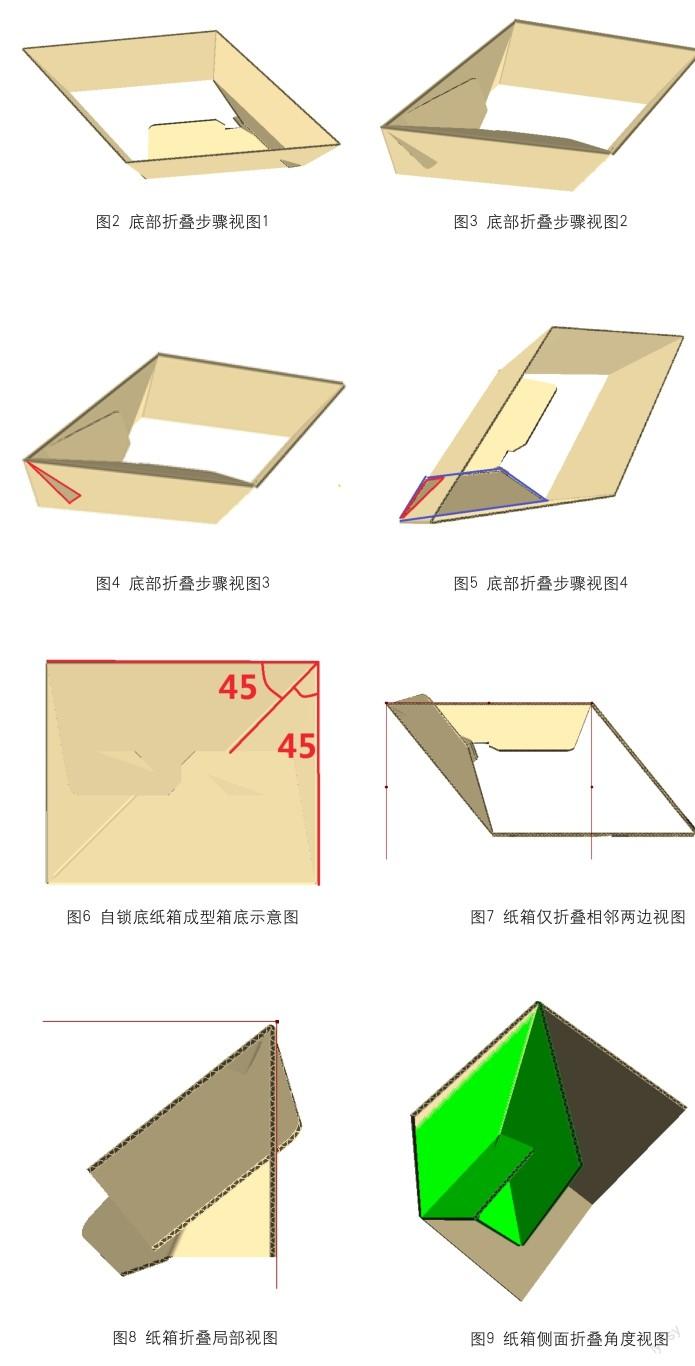
首先,假定自锁底纸箱底部正常自锁,箱底成型后的角度视图如图6所示。
其次,集中观察自锁底纸箱局部相邻两边纸板的不同角度折叠示意图,图7为纸箱仅折叠相邻两边,图8为纸箱折叠局部视图,图9为从顶面看折叠角度。其中,图9中黄色部分为未折叠展平状态,绿色部分为折叠过程中的箱底结构。
然后,将图9的视图效果定格在其底部结构的顶视图上,如图10所示,同时对相应的箱底进行几何线定义,并简化为图11。
接下来开始进行几何数学推演:
(1)定义简化图11中的结构形式为正方形,其边长为L,L为已知常数。
(2)投影面decg是底面dfjg沿着边cd往上折形成的,同时∠fdg也同步折成∠edg,在底面dfjg形成垂直投影。边dg不动,边fd移动成为边ed。
(3)三角形△cdg与三角形△cde分别是三角形△jdf与三角形△jdg往上折后的投影三角形。
(4)边de与边ce是边df与边fj旋转折叠后在面dfje上的投影,∠dfj为90°,则∠dec为90°,而∠dgc为90°,边dg=边de=L,共斜边dc;所以三角形△cdg与三角形△cde是完全相等的,三角形△cda与三角形△cdg又完全相等,所以三角形△cda与三角形△cde完全相等,可得到边ab与边eb相等。
之后推演计算公式:
(1)边长ab为纸板超出纸箱端面部分,需要去除,否则会形成纸板与箱体间的干涉,纸箱不能正常成型。
(2)设定边长ab=x,边长ad=y,边长bd=H,边长fd=dg=L。
(3)那么三角形△bad为直角三角形,其边长ed=边长dg=L。
由此可得:
x2+y2=H2 (公式1)
H=L-x (公式2)
(4)将公式2代入公式1可得:
x2+y2=(L-x)2→y2=L2-2Lx (公式3)
(5)当纸箱折叠平放时,公式3中y=0,那么x(x=L/2)为最大值,如果去掉L/2的距离,则可避免纸箱折叠过程出现干涉现象,如图12所示。
(6)进一步计算“L/2”,推算出自锁底纸箱底部结构角度约为26.7°,如图13所示。
案例验证
笔者又对两个不同角度的FEFCO0700箱型进行了实样成型验证。其中,样品A采用图13结构图制作而成,样品B采用图1结构图制作而成。图14为样品折叠过程对比图,图15为样品折叠成型后对比图。
从图14和图15中红色圆圈所指区域可明显看出,采用原结构图纸(图1)制成的样品B明显会出现纸板与箱体折叠干涉后的挤压压痕线;而样品A整个箱体都比较挺括,无任何额外压痕线。
事实证明将自锁底纸箱底部结构角度调整到26.7°,可有效避免纸板出现干涉现象。因此,应合理计算自锁底纸箱底部结构角度,不要一味沿用较小角度的结构设计,从而保证自锁底纸箱良好的外观及使用性能。

