区域供水管网覆盖特征的盒维数测度研究

晋良海，张再昌，边 星，吴菊华，尹 洁

(1.三峡大学水利与环境学院，湖北宜昌443002； 2.三峡大学安全生产标准化评审中心，湖北宜昌443002；3.水电工程施工与管理湖北省重点实验室，湖北宜昌443002)

区域供水管网覆盖特征的盒维数测度研究

晋良海1，2，3，张再昌1，边 星1，吴菊华1，尹 洁1

(1.三峡大学水利与环境学院，湖北宜昌443002； 2.三峡大学安全生产标准化评审中心，湖北宜昌443002；3.水电工程施工与管理湖北省重点实验室，湖北宜昌443002)

为解决区域供水管网分布不均造成居民用水分配不公的问题，按人口密度对供水管网进行分区规划，并建立管网覆盖特征的测度模型。采用盒维数法来表征区域供水管网覆盖形态，以标准区域覆盖深度为基准测算目标区域供水管网覆盖度，并以此作为评价供水管网布置合理性指标。实际应用表明，区域供水管网覆盖测度模型可以准确反映管网的分布特征和覆盖均匀度，覆盖度可作为评价区域供水管网规划是否公平合理的基本指标。

供水管网；分区；覆盖度；盒维数；测度

0 引 言

现行的供水管网评价指标一般采用覆盖密度，只能反映供水管网某区域的总体覆盖程度，不能度量复杂管网占有空间的有效性，也不能表现供水管网分布与区域人口散布密度匹配程度。区域管网空间分布的均匀程度直接关系到居民用水的公平性和便利性，制约着供水管网的效益发挥。若需改善供水管网空间分布的均匀性，必先建立管网空间分布均匀性的评价方法。分形理论可以透过线性不规则的形态，认清局部和整体之间的本质联系。Ying L[1]提出一种稳定的盒维数法，可以用来描述供水管网分布均匀性，能将供水管网外在性质的不规则性反映至其内在结构。

网结构的分形研究起源于路网。杨东援[2]采用分形几何学方法概述路网覆盖形态；唐建桥[3]和张铮[4]对交通路网覆盖形态特性进行研究，为描述网结构覆盖的深入程度、分布的均匀程度提供新的表现方法。我国供水管网的分形研究起步晚，近10多年取得了较为丰富的成果：苏欣[5]对城市污水再生回用系统布局规划进行研究；李晨等[6]提出了以包括供水、污水、雨水管网为对象的市政管网分形模型；吕鑑[7]和束庆年[8]提出了雨水管网分形模型；柳晓明[9]和赵鹏[10]将分形维数运用到区域供水管网系统；张明生[11]和程永前[12]以覆盖度作为排水管网评价指标，但没有进一步建立具体的分区模型。

以上成果将分形维数作为网结构工程规划设计的评价指标，没有考虑人口密度不同给网结构规划带来的变化，也没有进一步优化盒维数法计算的稳定性。基于此，本文对供水管网进行分区预处理，考虑人口密度的影响，提出以人口密度为基准将供水管网区域进行分类；再采用改进的分形理论中的盒维数法计算供水管网的覆盖度和覆盖深度，对供水管网空间规划的合理性进行评价。

1 供水管网分区规划的现状

供水管网是区域生产生活的血脉。如何布置供水管网是供水工程必须解决的首要问题，关系到区域居民生活用水是否达标、用水量分配是否均衡。传统的供水管网规划方法仅凭经验和流量分别确定管段走向和管径，提出几个方案进行对比分析[13]。而供水管网实际情况非常复杂，且规划人员主观判断规划供水管网缺乏定量科学依据，易造成区域之间供水管网分布不均。部分区域供水管道布置冗多，引起资源浪费；部分区域供水管道布置不完善，难以满足区域居民的实际用水需求。如，重庆市渝北区和垫江县人口密度均为590人/km2，渝北区人均年生活用水量达到1 318 m3，而垫江县仅为242 m3。根据GB/T 50331—2002《城市居民生活用水量标准》，重庆市居民人均年生活用水量标准为438～601 m3[14]。以上数据可以看出，重庆市供水管网区域分布差异大，现行供水管网规划存在很大的局限性。

运用盒维数法建立区域供水管网覆盖测度模型，计算得到的覆盖度和覆盖深度可以准确反映管网的分布特征和覆盖均匀度。以覆盖度和覆盖深度为基本指标，对区域供水管网进行规划，可以很好地解决上述问题。

2 供水管网覆盖度的盒维数描述

用边长为R的正方形覆盖供水管网整体分布范围，然后将边长R不断等分(第1次分成2等分，第2次分成3等分，依次类推)，将正方形分为若干份等大小的网格。取第i次等分后网格的边长为ri，其中有供水管网覆盖的网格数为N(ri)，于是得到随i变化的函数ri以及N(ri)。本文用[r，N(r)]曲线的变化率来定义相似维数，即分形维数D(ri)，表示第i次分区后有供水管网通过的网格的覆盖程度。公式如下

为了便于计算，可将上式改进为

i取不同值时D(ri)随N(ri)变化见图1。从图1可以看出，D(ri)的取值范围为[0，2]。有供水管网通过的网格数越多，表示细分后的网络与原网络的相似程度越高，D(r)值也越大，供水管网的覆盖特征也就越好。供水管网覆盖度反映了供水管网覆盖的完善程度。

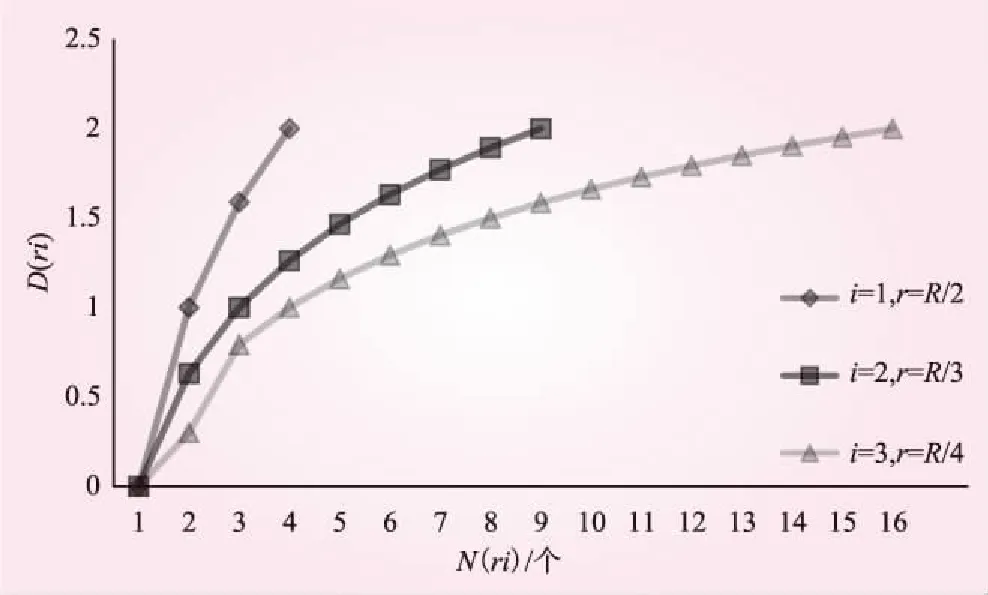
图1 i取不同值时D(ri)随N(ri)变化

ri确定时，随着N(ri)值的不断增大，D(ri)值也不断增大，即确定网格规划后，有供水管网通过的网格数越多，供水管网覆盖特征的分形维数越大，则其覆盖越均匀；随着ri的不断减小，D(ri)的取值区间不断细化，即测算供水管网覆盖特征的分形维数的精度不断提高。结合图1，当1.661≤D(r)≤2时，即2/3及以上网格中仍有供水管网通过，则称该供水管网具有基本覆盖相似特征。覆盖度D(r)=1.661可以作为判断该区域供水管网布置是否合理、功能是否完善的基本标准。

当网格边长r继续缩小，供水管网出现不再具有覆盖度D(r)=1.661的基本标准的临界状态，此时的网格边长r=r临界定义为该区域供水管网的覆盖深度。供水管网覆盖深度r临界表示的是该区域约有2/3的小网格中有供水管网通过的最小网格边长，也表示平均相隔多少距离就有供水管网通过。覆盖深度越小，说明相隔的供水管网之间的距离越小，供水管网的覆盖状况越好；覆盖深度越大，说明相隔的供水管网之间的距离越大，供水管网的覆盖状况越差。

在供水管网建设中，人口密度是重要的决定因素。人口密集的地区要求供水管网的铺设更为发达。现构造一个供水管网评价系统，取供水系统非常成熟的甲城市，各区域(根据人口密度大小分为Ⅰ～Ⅴ型供水区域)人均年生活用水量都非常均衡，且都在标准值范围内。用盒维数法算出甲城市Ⅱ型供水区域的供水管网覆盖度为D(r)=1.661时的覆盖深度R，即最少相隔Rm有1条供水管通过时，该区域的供水管网覆盖特征良好。将该标准运用到乙城市中，即反过来用盒维数法算出乙城市Ⅱ型供水区域第i次分区后的边长ri=R时，对应的供水管网覆盖度D(ri)。当1.661≤D(ri)≤2时，说明乙城市Ⅱ型供水区域供水管网覆盖特征良好。供水管网评价方法见图2。

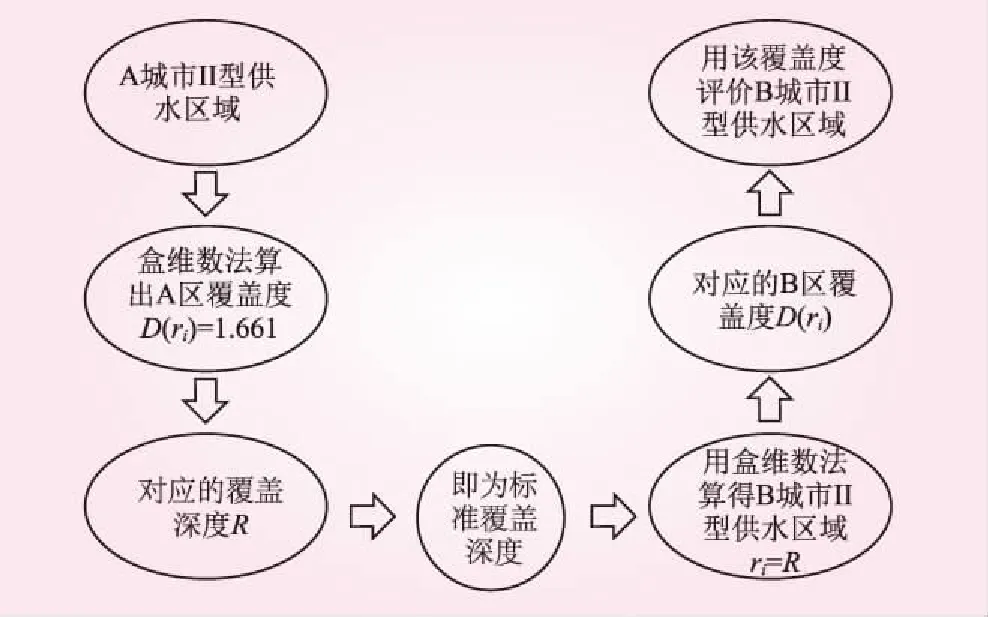
图2 供水管网评价方法

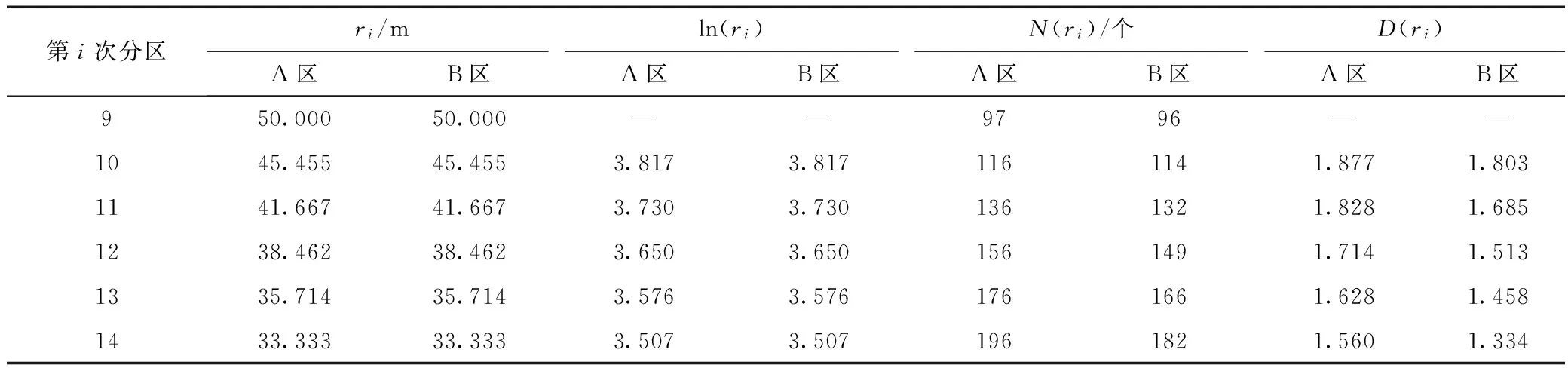
表2 盒维数法第9～14次等分

3 工程案例

某城市供水管网布置见图3。根据供水管网分区管理模式，将图3中供水管网分成面积相等的A、B、C区。其中，A、B区人口密度相同，同属于Ⅱ型供水区域，而其管网分布型式却有差异，这里认为A区供水管网分布较为合理。

图3 某城市供水管网布置

利用盒维数法分析A、B区。第1次将供水区域等分成2份，第2次等分成3份，依次类推。图4为第9～14次盒维数法等分图例。表2为等分结果。

图4 盒维数法第9～14次等分图例

图5 D(ri)与ln(ri)关系

D(ri)与ln(ri)关系见图5，从图5可知，A区数列ln(ri)与数列D(ri)间的相关系数r=0.992，大于其临界值r0.05(2，5)=0.754，表明两数列间的关系密切，存在显著线性关系；B区相关系数r=0.993，大于其临界值r0.05(2，5)=0.754，两数列同样线性相关。A区一元线性回归方程设为D(ri)=a+bln(ri)，利用最小二乘法估计回归系数，计算公式如下

求出A区一元线性回归方程为D(ri)=1.074 ln(ri)-2.204。覆盖度D(r)=1.661可以作为判断该区域供水管网布置是否合理、功能是否完善的基本标准。当D(ri)=1.661时，ln(ri)=3.599，覆盖深度ri为36.562 m。

B区一元线性回归方程设为D(ri)=c+dln(ri)，利用最小二乘法估计回归系数，计算公式

求出B区一元线性回归方程为D(ri)=1.507 ln(ri)-3.951。当覆盖深度ri为36.562 m时，算出B区覆盖度ln(ri)=1.473。

A区供水管网分布合理，算得的A区管网覆盖深度ri为36.562 m，说明此人口密度的地区中，大部分区域相邻两条供水管道间距约为36.562 m时，该地区的供水管网能很好地满足居民的生活用水需求。A区和B区人口密度相同，为同一类型供水区域，故而B区相邻两条供水管道间距约为36.562 m时，能满足居民生活用水的标准。B区ri=36.562 m时的覆盖度ln(ri)=1.473<1.661，表明B区能够达到供水标准的区域不足2/3，即B区供水管网布置有待加强和完善。

4 结 语

目前，区域供水管网布局规划缺乏科学依据，导致供水管道布置不均。以某一供水管网布置良好的城市为标准，用盒维数法计算出被评价地区的供水管网覆盖度，作为衡量该地区供水管网覆盖特征指标具有现实意义。对2个人口密度相同的区域建立模型分析比较表明，覆盖度可以很好地反映区域供水管网的覆盖特征。

本次案例分析中，用盒维数法计算过程较为繁杂，随着网格的增加，人为判断是否有网格通过会耗费大量时间，用盒维数法计算供水管网覆盖特征效率会大大降低。此外，该方法的计算机仿真模型还有待进一步开发。

[1]YING L， JIANGLI L， KE C. A Stable Algorithm of Box Fractal Dimension and Its Application in Pore Structure[J]. Rare Metal Materials and Engineering， 2015， 44(4)： 800-804．

[2]杨东援， 吴海燕， 宗传苓. 采用分形几何学方法概述路网覆盖形态[J]. 中国公路学报， 1996， 9(3)： 31-37．

[3]唐建桥， 左大杰， 王慈光. 基于分形维数的交通路网覆盖形态特性研究[J]. 公路交通科技， 2014， 31(4)： 114-119， 158．

[4]张铮， 陈亮， 魏洪涛. 基于分形理论的区域路网覆盖性评价研究[J]. 河北工业大学成人教育学院学报， 2005， 20(1)： 10-13．

[5]苏欣. 城市污水再生回用系统布局规划研究[D]. 天津： 天津大学， 2012．

[6]李晨， 蔡丽. 市政管网的优化设计研究[J]. 才智， 2009(3)： 201．

[7]吕鑑， 杨向平， 束庆年， 等. 分形理论研究雨水管网分布[J]. 北京工业大学学报， 2003， 29(4)： 447-450．

[8]束庆年， 吕鑑， 郝二成， 等. 雨水管网的分形研究[J]. 中国给水排水， 2003， 19(9)： 57-59．

[9]柳晓明， 王圃， 甘福宁. 分形理论在城市给水管网布置中的应用[J]. 水资源与水工程学报， 2011， 22(3)： 92-94， 98．

[10]赵鹏， 张宏伟， 田一梅. 给水管网的分形特征研究[J].给水排水，2007，33(8)：117-121．

[11]张明生. 分形学理论在城市排水管网中的应用研究[J]. 西北大学学报： 自然科学版， 2010， 40(4)： 734-736．

[12]程永前， 宋乾武， 张玥， 等. 排水管网规划评价指标体系构建及分形维数应用[J]. 环境科学研究， 2011， 24(4)： 446-451．

[13]周连波. 基于分形的城市供水系统规划研究与应用[D]. 哈尔滨： 哈尔滨工业大学， 2013．

[14]蔡长赓. 《城市居民生活用水量标准》发布实施[J]. 给水排水， 2003， 1(2)： 19．

(责任编辑 杨 健)

Study on District Water Supply Network Coverage Based on Box-Counting Method

JIN Lianghai1,2, 3, ZHANG Zaichang1, BIAN Xing1, WU Juhua1, YIN Jie1

(1.College of Hydraulic & Environmental Engineering, China Three Gorges University, Yichang 443002, Hubei, China;2.Evaluation Center for Safety Production Standardization, China Three Gorges University, Yichang 443002, Hubei, China;3.Hubei Key Laboratory of Cascaded Hydropower Stations Operation & Control, Yichang 443002, Hubei, China)

In order to solve the problem of unfair regional water consumption caused by uneven urban water supply network geographic distribution, the water supply network is partitioned to planning according to population density and the measurement model of water supply network is established. The box-counting method is introduced to analyze the coverage characteristic of regional water supply network and the covering degree of regional water supply network in target area is calculated based on the covering depth of standard area. The covering degree is used as an indicator to judge whether the water supply network layout reasonable or not. The application research results show that the measurement model of regional water supply network based on covering degree can accurately reflect the distribution and uniformity of regional water supply network and the covering degree can be as a basic indicator to plan regional water supply network．

water supply network; partition; covering degree; box-counting method; measurement model

2016-06-13

湖北省自然科学基金资助项目(2014CFB690)

晋良海(1973—)，男，四川简阳人，副教授，博士，主要从事水利水电建设项目运筹、施工作业安全工效研究；张再昌(通讯作者)．

TU991.33

A

0559-9342(2016)11-0099-04