广播星历下多系统卫星位置、速度计算及精度分析
2016-02-25党亚民宋传峰
吴 波,党亚民,杨 强,宋传峰
(中国测绘科学研究院,北京 100830)
Precision Analysis of Satellite Position and Velocity by Multi-system
Broadcast Ephemeris
WU Bo,DANG Yamin,YANG Qiang,SONG Chuanfeng
广播星历下多系统卫星位置、速度计算及精度分析
吴波,党亚民,杨强,宋传峰
(中国测绘科学研究院,北京 100830)
Precision Analysis of Satellite Position and Velocity by Multi-system
Broadcast Ephemeris
WU Bo,DANG Yamin,YANG Qiang,SONG Chuanfeng
摘要:目前GNSS空间部分主要由GPS、GLONASS、Galileo、BDS 4系统构成,在利用广播星历进行多星组合导航时,需要根据不同卫星星座广播星历精度信息实现多系统定位信息的组合。现有研究对GPS、GLONASS广播星历精度进行了充分分析,但对由Galileo、BDS广播星历计算卫星位置、速度及其精度的研究相对较少。本文利用精密星历对GNSS广播星历计算的卫星位置、速度精度进行了分析。结果表明,GPS广播星历解算的卫星位置误差小于2 m,GLONASS广播星历解算的卫星位置误差最大在4 m左右,Galileo广播星历解算的卫星位置误差最大在3 m左右,BDS广播星历解算的GEO卫星位置误差最大在40 m左右,IGSO卫星位置误差最大在9 m左右,MEO卫星位置误差最大在5 m左右。GPS、Galileo、BDS速度误差在1 mm/s内,GLONASS速度误差在2 mm/s内。
关键词:广播星历;精密星历;坐标变换;时间变换;精度
目前全球导航卫星系统(GNSS)主要有美国的GPS、俄罗斯的GLONASS、欧洲的Galileo、中国的BDS。卫星星历按使用来源可分为广播星历和精密星历。在卫星导航中,实时确定用户的位置一般依靠卫星广播星历计算卫星位置,卫星星历误差是单点定位的主要误差源之一。在多星定位系统中,评估广播星历的精度是进行实时多星组合定位的重要基础。
精密星历是由有关科学或服务组织经过处理后提供的一种事后星历。由于精密星历生成时间较晚,必须于事后13 d才能得到,因此在用户实时导航定位中广泛使用广播星历。已有许多文献对GPS、GLONASS广播星历精度进行了比较分析[1-5],但是对由Galileo、BDS广播星历计算卫星位置、速度及其精度的研究相对较少。
本文利用上述4个卫星系统的广播星历,分别计算各系统中卫星的位置、速度,将地壳动力学数据信息系统(CDDIS)上公布的GNSS精密星历作为真值,基于GNSS系统间坐标变换和时间系统变换,对多系统广播星历精度进行评估,并分析对比了不同卫星系统广播星历解算卫星位置的误差。
一、广播星历解算卫星位置、速度
1. 数学模型
已有相关文献对利用GPS、GLONASS广播星历计算卫星位置、速度的方法进行了详细说明[2-3],在此不再赘述。Galileo卫星和BDS系统中IGSO、MEO卫星位置、速度的计算方法与GPS一致,BDS系统中的GEO卫星,因其静地属性,在计算卫星位置时,需要对已求出的坐标再添加旋转,最终得到其真实位置。具体公式如下[6-7]
(1)
式中,

2. 必要条件
(1) 统一时间系统[8]
不同GNSS系统一般使用独立的时间系统,如GPST、GLONASST、GST、BDT,而CDDIS上公布的精密星历采用的时间系统是GPST,为进行精度比较,在计算卫星位置时,必须首先将时间系统统一到GPST。GPS、GLONASS、Galileo、BDS 4系统间时间转换关系可参考文献[8]。
(2) 统一坐标系统[8]
GPS广播星历采用的坐标系统是WGS-84,GLONASS广播星历采用的坐标系统是PZ-90,Galileo广播星历采用的坐标系统是GTRF,BDS广播星历采用的坐标系统是CGCS2000,而CDDIS上公布的精密星历坐标系统采用的是ITRF2008瞬时历元下的,为便于下一步精度比较,在计算卫星位置时,需要将坐标系统统一到ITRF2008下。在一定精度范围内WGS-84、GTRF坐标系可认为与ITRF2008等价,CGCS2000坐标系目前与ITRF2008的差异也在广播星历精度范围内,因此只需将PZ-90坐标系转为WGS-84坐标系即可,坐标转换关系可参考文献[8—10]。
二、算例分析
广播星历每2 h提供一组轨道参数,每组轨道参数之间存在一个跳变[4];由于精密星历是事后处理得到的,可以认为精密星历中各个时刻的卫星坐标间不存在跳变,因而可以作为真实值[5]。
为比较分析上述不同GNSS广播星历轨道精度,本文采用了2014年7月24日(年积日205天)GPS、GLONASS、Galileo、BDS的广播星历数据,并采用CDDIS网站提供的以上4系统的精密星历数据(GPS、GLONASS由IGS提供,Galileo由德国慕尼黑工业大学提供,BDS由德国波茨坦地学研究中心GFZ提供)。由于广播星历的时间间隔是2 h,精密星历是15 min,两者的时间不一一对应。为方便对比,同时为了减少内插方法的影响,直接利用广播星历计算输出15 min间隔的卫星位置,而后以精密星历的结果作为基准,评定广播星历的解算精度。
由于当前精密星历通常不包含速度信息,为了分析由广播星历计算的卫星速度精度情况,首先拼接3 d的精密星历,然后利用12阶滑动拉式插值法对上述星历进行插值,求得当天任意时间点的速度,最后以该值作为基准,评定由广播星历算得的卫星速度的精度[1]。
下面仅以GPS 1、10、20、24星,GLONASS 1、7、17、23星,Galileo 11、19星,BDS 1、5、9、14星为例,绘制它们在一天内轨道误差、速度误差变化图,分别如图1—图4所示,其中,ΔX、ΔY、ΔZ分别表示由广播星历解算的卫星位置与精密星历卫星位置结果之差,单位为m;ΔVx、ΔVy、ΔVz分别表示由广播星历解算的卫星速度与由精密星历生成的卫星速度结果之差,单位为mm/s。
各系统广播星历解算误差结果如图1—图4所示,其中横轴表示96个(24×4个/小时)历元。
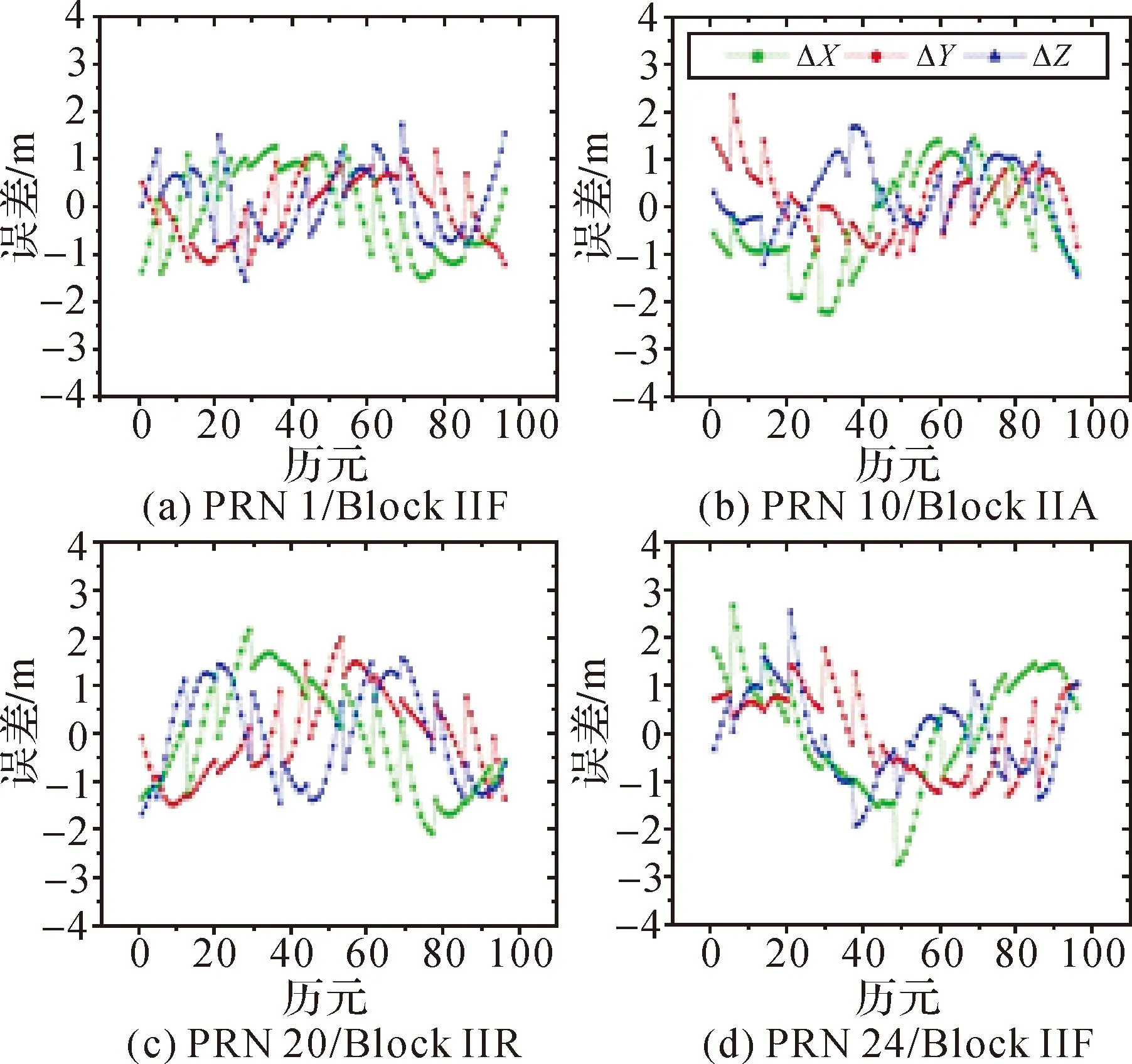
图1 GPS广播星历位置误差

图2 GLONASS广播星历位置误差
为了分析广播星历一天内轨道误差变化趋势,本文在进行广播星历与精密星历间轨道偏差的比较后,进行了统计分析。首先计算每天各颗卫星各时刻在3个方向上的偏差,然后分别统计每天在3个方向上的平均值(mean)和均方根差(RMS),具体计算公式如下
(2)
式中,biasijk为某系统第i颗卫星j时刻在k方向上的偏差;n为所有有效偏差结果个数;k=1,2,3,分别对应于X、Y、Z方向。
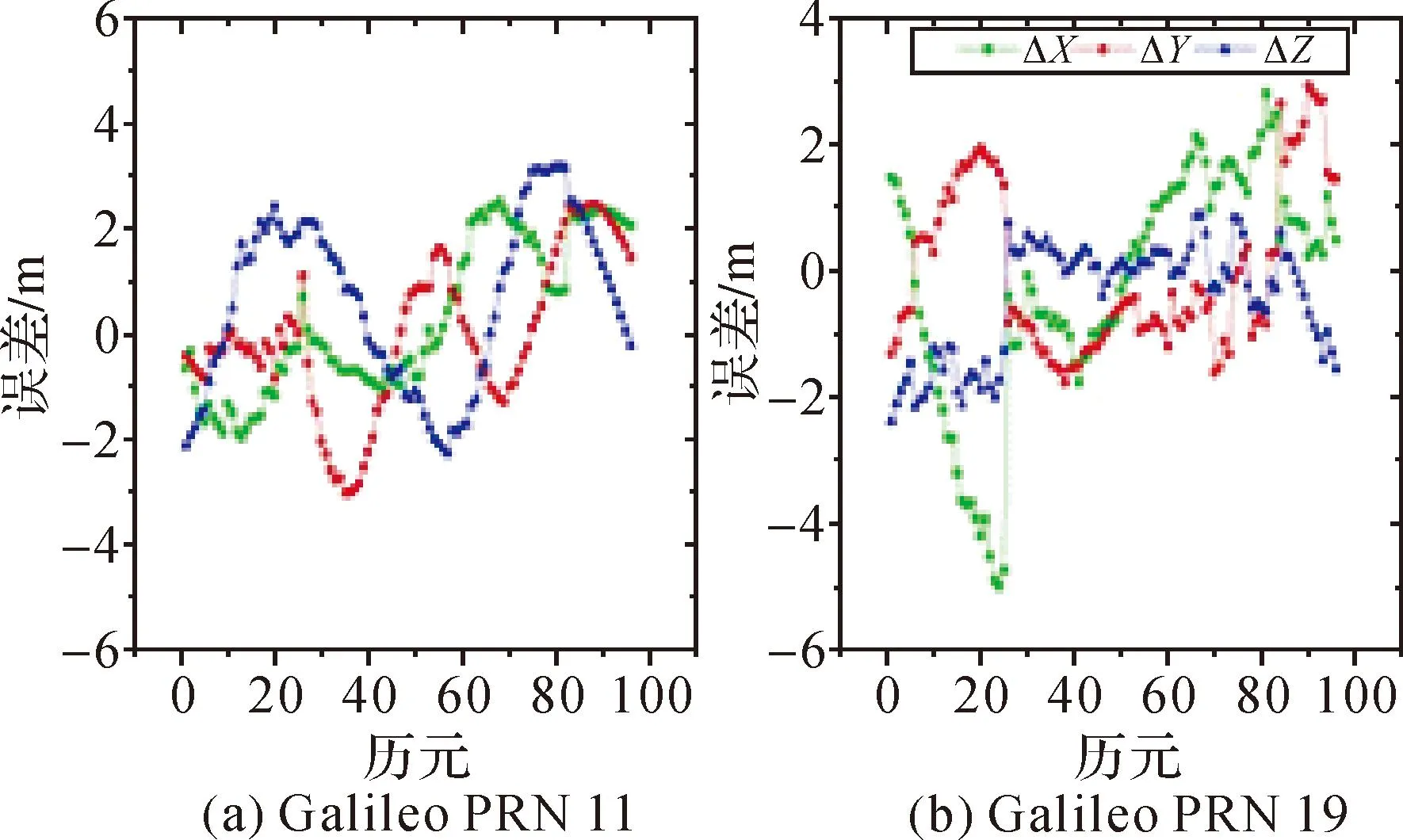
图3 Galileo广播星历位置误差

图4 BDS广播星历位置误差
由图1—图4可知,GPS广播星历3方向解算误差在2 m左右;GLONASS广播星历3方向解算误差大部分卫星在2 m左右,个别卫星解算误差稍大,在4 m以内;Galileo广播星历3方向解算误差也在2 m左右;BDS系统中,GEO卫星轨道误差最大可达40 m左右,IGSO、MEO卫星轨道误差最大在10 m以内,其中,Z向的轨道误差变化最稳定,同时也最小。
单天中4系统各颗卫星3个方向上的日平均值和RMS变化如图5—图8所示。
GPS、GLONASS、Galileo、BDS系统卫星总数分别为32、24、4、14,图5—图8中部分卫星由于导航文件中没有相关记录,故而未在图中表示。
从图5—图8中可以看出,GPS、GLONASS、Ga-lileo广播星历的轨道误差在3个方向的日平均值均在0附近,其中GPS性能最优,GLONASS、Galileo次之。BDS的GEO卫星,因其静地属性及不定期的机动调整,其轨道误差较大,以1号星、4号星为代表,3方向中误差最大可达40 m左右。MEO、IGSO卫星轨道误差明显优于GEO卫星,IGSO卫星整体水平在4 m左右,MEO卫星最优,大约在2 m左右。

图5 GPS卫星位置误差统计

图6 GLONASS卫星位置误差统计
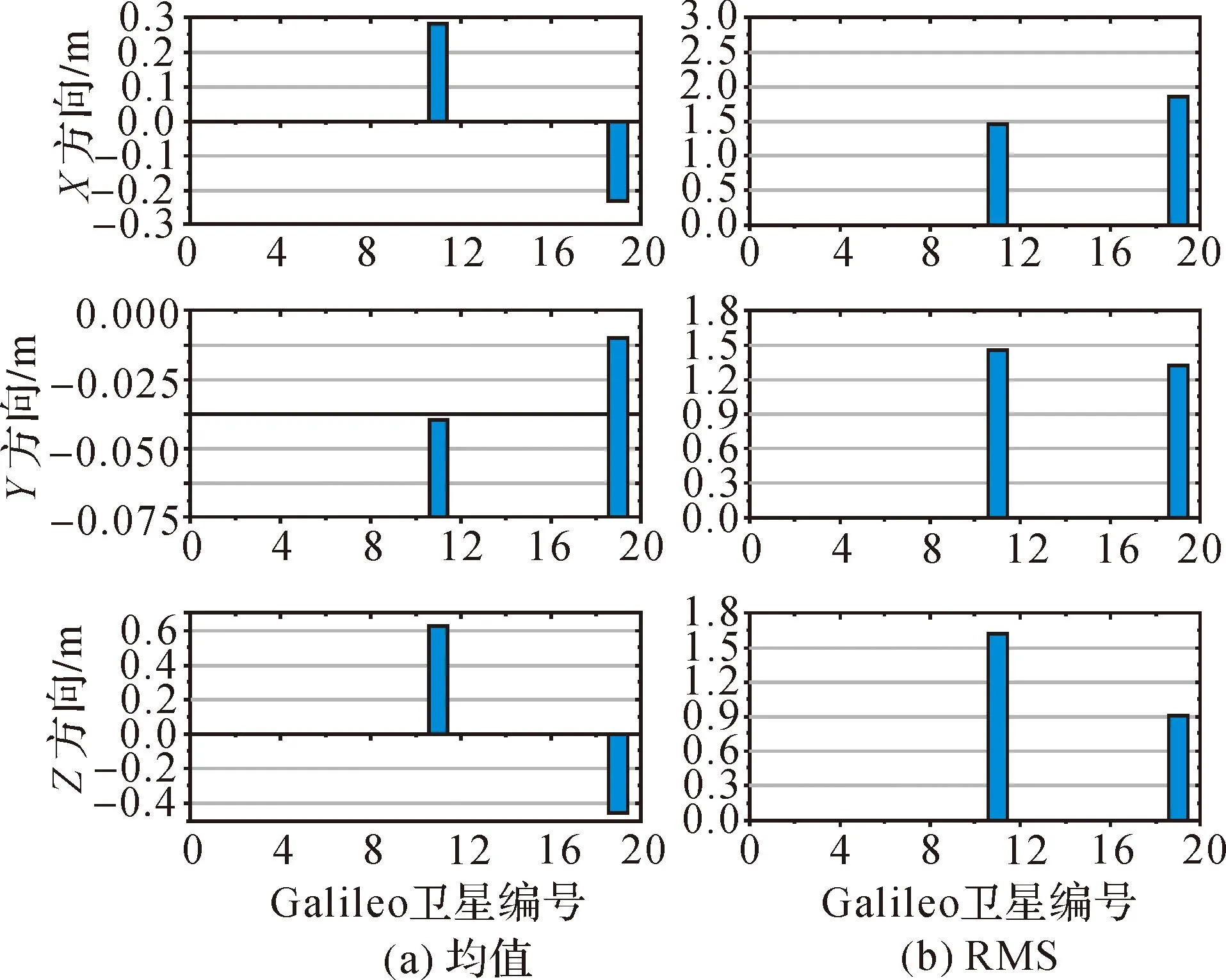
图7 Galileo卫星位置误差统计
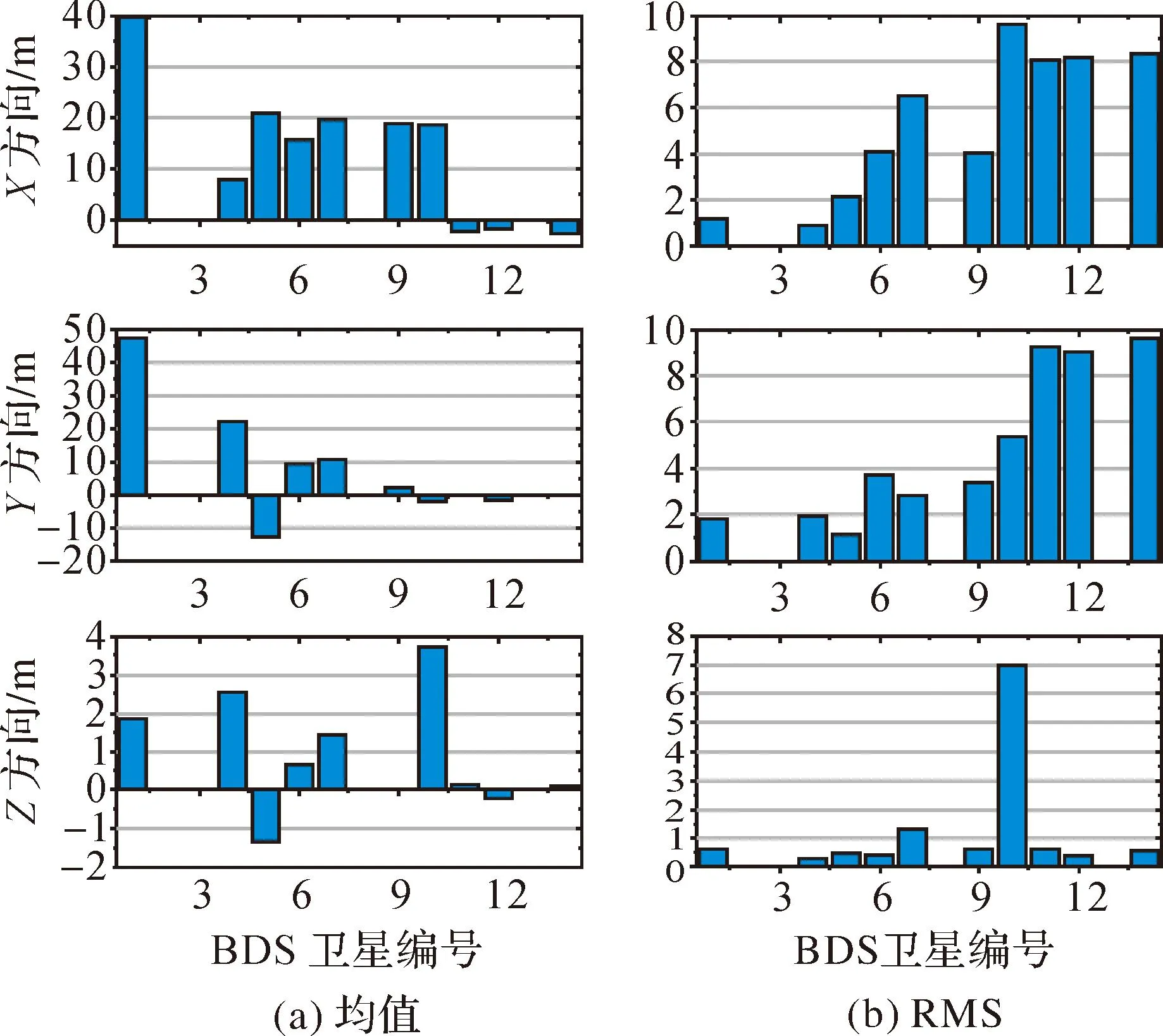
图8 BDS卫星位置误差统计
上述4系统中Z方向的RMS明显优于另外两方向,且GPS、GLONASS较稳定。
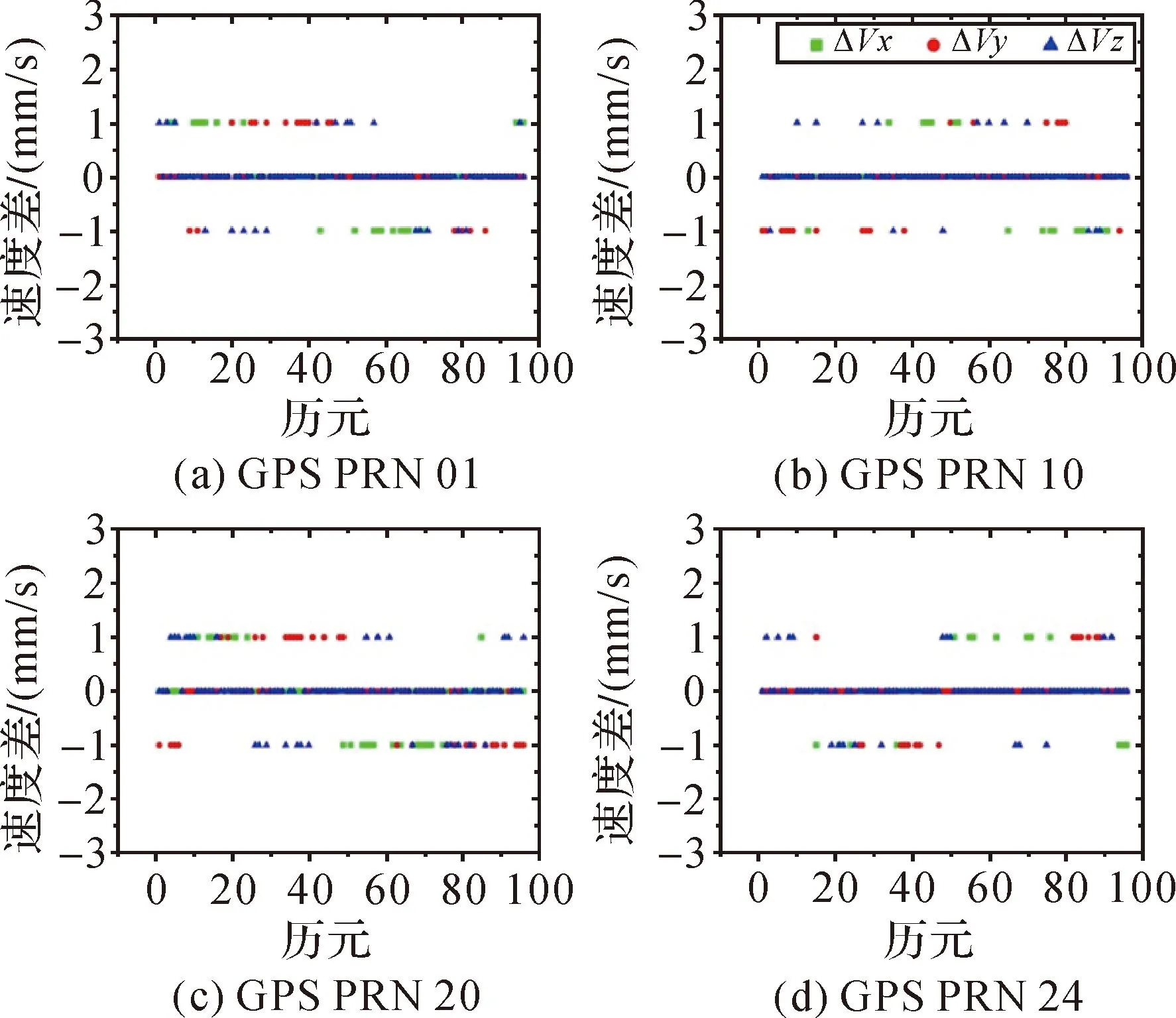
图9 GPS 广播星历速度误差
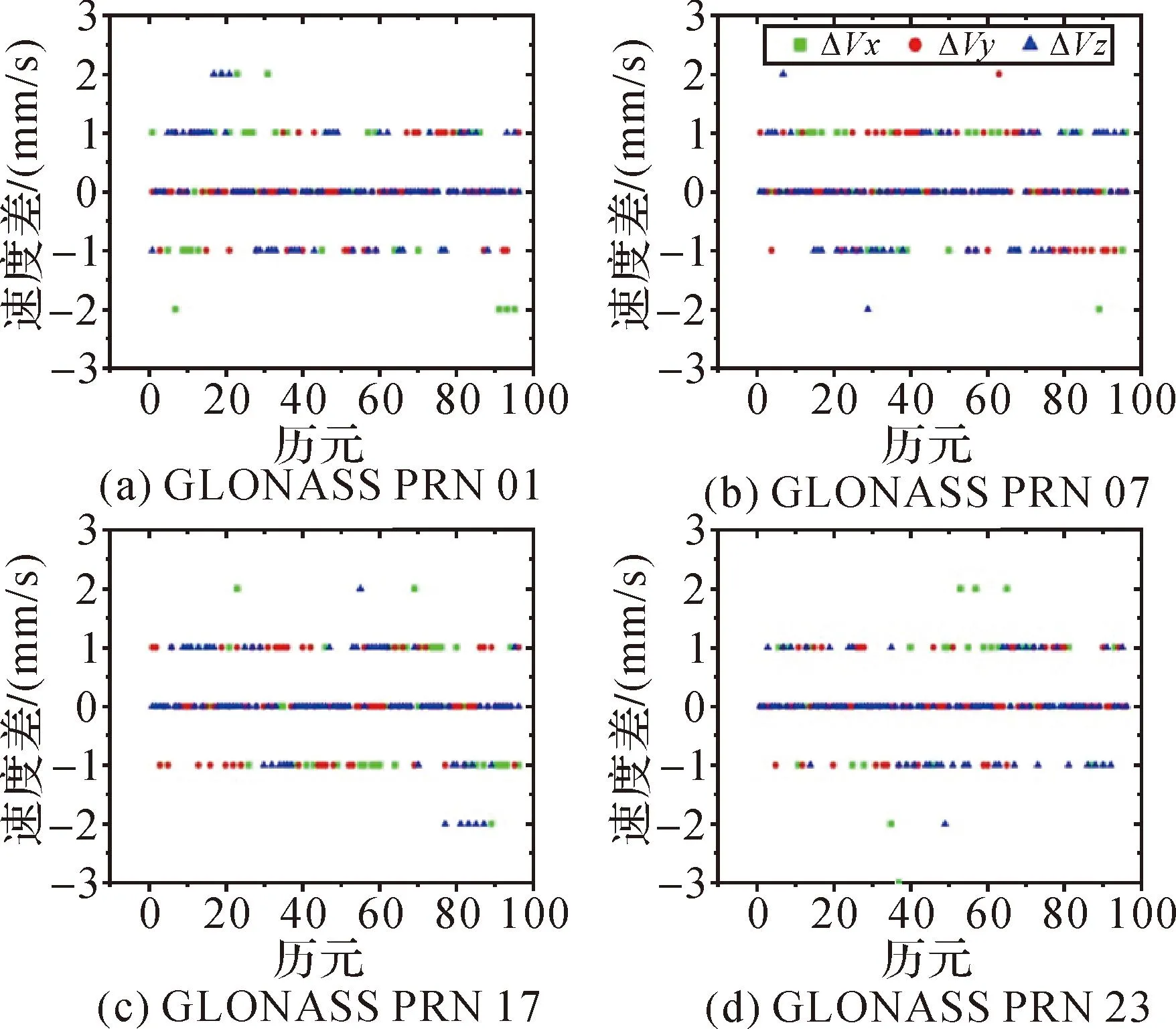
图10 GLONASS广播星历速度误差
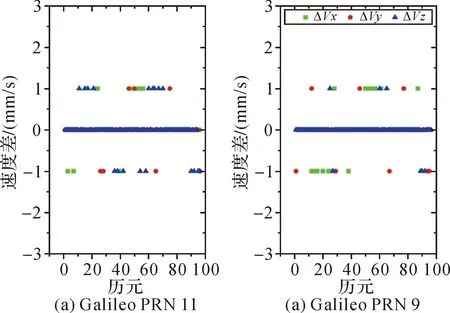
图11 Galileo广播星历速度误差
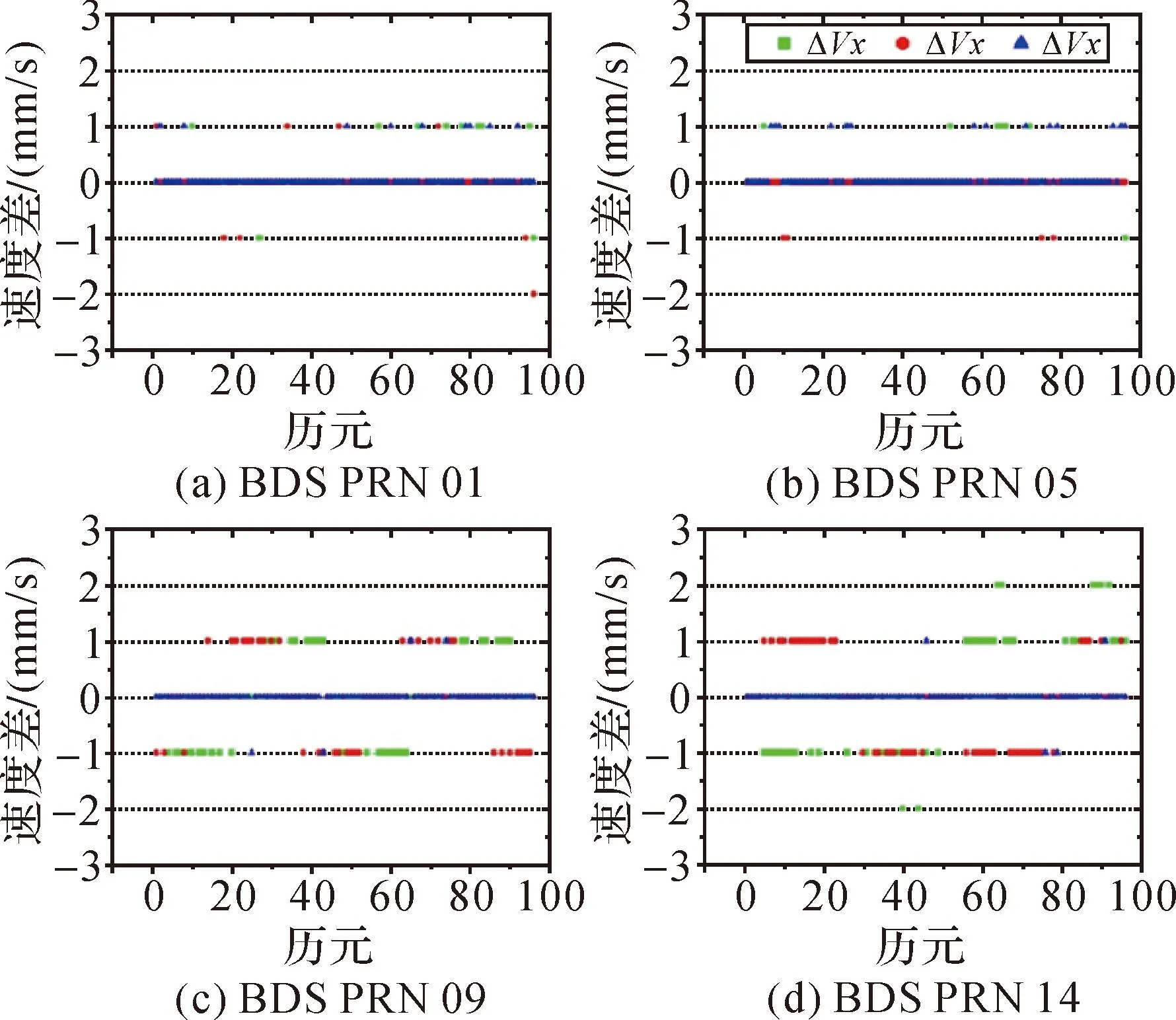
图12 BDS广播星历速度误差
三、结论
1) 由广播星历解算的GPS、GLONASS、Galileo卫星位置误差大多数在2 m左右,综合考虑单天误差变化的大小,卫星RMS值,GPS系统性能最优,GLONASS、Galileo次之。
2) 由广播星历解算的BDS GEO卫星位置误差最大在40 m左右,IGSO卫星位置误差最大在9 m左右,MEO卫星位置误差最大在5 m左右。
3) 由广播星历解算的GPS、Galileo、BDS卫星速度误差在1 mm/s内,GLONASS卫星速度误差在2 mm/s内。
4) 算例结果进一步证明了由广播星历解算卫星位置、速度方法的正确性。
本文仅选取1天数据进行试验,并未选用长周期数据进行解算,同时,未考虑广播星历外推时间不同对解算结果的影响,以上这些问题有待进一步分析研究。
参考文献:
[1]刘伟平,郝金明,李作虎.由广播星历解算卫星位置、速度及精度分析[J].大地测量与地球动力学,2010,30(2):144-147.
[2]洪靖,高才,汤亮.GPS/GLONASS导航定位中卫星位置和速度的计算[J].数字通信,2011(2):67-70.
[3]刘磊,盛铮,王迎强,等.利用广播星历计算GPS卫星位置及误差分析[J].解放军理工大学学报(自然科学版),2006,7(6):592-596.
[4]李征航,丁文武,李昭.GPS广播星历的轨道误差分析[J].大地测量与地球动力学,2008,28(1):50-54.
[5]王霞迎,秘金钟,张德成,等.GPS广播星历位置、速度和钟差精度分析[J].大地测量与地球动力学,2014,34(3):164-168.
[6]中国卫星导航系统办公室.北斗卫星导航系统空间信号接口文件公开服务信号B1I(1.0版)[EB/OL].[2012-12-01](2013-03-01).http:∥www.beidou.gov.cn/.
[7]党亚民,秘金钟,成英燕.全球导航卫星系统原理与应用[M].北京:测绘出版社,2007.
[8]王世进,秘金钟,谷守周,等.BDS/GPS组合相对定位方法及精度分析[J].测绘通报,2014(5):1-4.doi:10.13474/j.cnki.11-2246.2014.0144
[9]刘庆元,包海,王虎,等.GPS、GLONASS、GALILEO三大系统间时间系统以及坐标系统的转换[J].测绘科学,2009,33(5):13-15.
[10]魏子卿.2000中国大地坐标系及其与WGS84的比较[J].大地测量与地球动力学,2008,28(5):1-5.
[11]林吉兆,贾登科,武警.CGCS2000及WGS84坐标系若干问题探讨及应对策略[J].水运工程2014(2):27-30.
引文格式: 吴波,党亚民,杨强,等. 广播星历下多系统卫星位置、速度计算及精度分析[J].测绘通报,2016(1):64-67.DOI:10.13474/j.cnki.11-2246.2016.0016.
作者简介:吴波(1989—),男,硕士生,主要研究方向为高精度GNSS数据处理。E-mail:455722104@qq.com
收稿日期:2014-12-12
中图分类号:P228
文献标识码:B
文章编号:0494-0911(2016)01-0064-04
