奇异值分解法在病态问题中的应用

徐　文，陈　义，游　为

(1. 同济大学测绘与地理信息学院，上海 200092； 2. 西南交通大学地球科学与

环境工程学院，四川 成都 610063)

Application of SVD Method in Ill-posed Problem

XU Wen，CHEN Yi，YOU Wei



奇异值分解法在病态问题中的应用

徐文1，陈义1，游为2

(1. 同济大学测绘与地理信息学院，上海 200092； 2. 西南交通大学地球科学与

环境工程学院，四川 成都 610063)

Application of SVD Method in Ill-posed Problem

XU Wen，CHEN Yi，YOU Wei

摘要：用截断奇异值分解法和修正奇异值分解法对大地测量病态问题进行了处理，并与最小二乘的结果进行了比较，最后将两者方法进行结合同样对病态方程进行了处理，得到了结合奇异值分解的解，并与截断奇异值、修正奇异值分解的解以及真值进行比较，发现结合奇异值分解的解即修正奇异值截断法比截断奇异值和修正奇异值的解更加靠近于真值，修正奇异值截断法相比于截断奇异值和修正奇异值法对于病态方程抗干扰能力更强，更具有实际意义。

关键词：病态方程；奇异值分解；截断奇异值；修正奇异值

在测量平差中, 当误差方程式的系数矩阵或常数向量有微小的误差扰动时，就会引起解的剧烈波动，从而导致计算出来的结果与真值相差比较大，这种问题就称为病态问题，对应的矩阵称为病态矩阵。病态矩阵表现为矩阵的行列式等于或接近于零，或者矩阵的行或列向量存在近似的线性相关。矩阵奇异值分解是一种对误差方程的系数矩阵直接进行分解来求取未知数最小二乘解的比较实用的解法。近年来病态问题的处理在大地测量的数据处理中得到了越来越广泛的应用。在病态问题中，法方程式系数矩阵的条件数是误差方程系数矩阵条件数的平方,对误差方程式的系数矩阵进行处理有利于降低方程的病态性，使得未知数的估值更加接近于真值。在非病态方程的条件下,矩阵的奇异值分解算法和最小二乘算法所得到的结果一致。而在病态方程条件下, 对于相对较小的奇异值截断去掉，或者对全部或部分奇异值进行修正，使得奇异值或者将二者相结合的方法相对更加紧凑，就可以达到减少均方根误差、提高未知数的精度和可靠性的目的，从而获得更为准确的解[1-2]。

一、病态方程的解法

定理1设m×n矩阵A∈Rm×n(Cm×n)，矩阵A的秩rank(A)=r(r>0),r≤{m,n}，则存在m阶正交(酉)矩阵U和n阶正交(酉)矩阵V，使得[3-4]

(1)

式中，Σ=diag(σ1,σ2,…,σr)，且σ1≥σ2≥…≥σr>0，而σi(i=1,2,…,r)为矩阵A的非负奇异值。式(1)称为矩阵A的奇异值分解式[1,3]。

1. 截断奇异值分解

在病态方程问题中未知数的最小二乘解有较大波动的主要原因是：误差方程式的系数矩阵有等于或接近于0的奇异值。一个最直接的做法就是去掉那些等于或接近于0的奇异值，用损失未知数的无偏性为代价来换取均方根误差的减小。假设去掉接近于0的t-k个奇异值, 就可以得到截断奇异值的解, 即

(2)

这其中的关键问题是如何选择合适的截断参数k，在有关文献中关于截断参数k的选择方法有L曲线法、F假设检验法、极小化均方误差法等。本文用L曲线法来求解截断参数，求出截断时所对应的奇异值所在的下标数值i，最后得到的截断奇异值法的解为

(3)

式中，V1为矩阵V的前i列；D1为矩阵Σ的前i×i的矩阵；U1为矩阵U的前i列[1-2]。

2. 修正奇异值分解

奇异值分解中，相对较大的奇异值表示比较可靠和肯定的部分，而相对较小的奇异值则表示浮动较大、不那么可靠的部分。截断奇异值分解法就是去掉那些相对较小奇异值，奇异值分解法还可以通过修正奇异值的方法，适当地增大那些接近于0 的奇异值，减小那些相对较大的奇异值，使得奇异值相对更加紧凑。杨文采提出了一种修正奇异值分解方法，设t为截断奇异值法所保留的最小奇异值的限值, q为小于t的奇异值个数, 则相应的修正方案为[1]

(4)

得到修正后的奇异值法的未知数解为[2]

(5)

式中，Dλ=diag(λ1，λ2，…，λm)。

3. 修正奇异值截断法

修正奇异值截断法就是先对所有奇异值进行修正，根据式(4)、式(5)适当地增大那些接近于0 的奇异值，减小那些相对较大的奇异值，使得奇异值相对更加紧凑；然后再进行截断，用损失未知数的无偏性为代价来换取均方根误差的减小，使得更加接近于真值。

二、 病态方程算例

文献[2]第五章中克服病态性的改进算法研究实例5.2对其矩阵的条件数为128 920，病态严重，5个未知数的真值为x=[11111]T,进行AATA处理[5]，使其病态性更强，见表1。

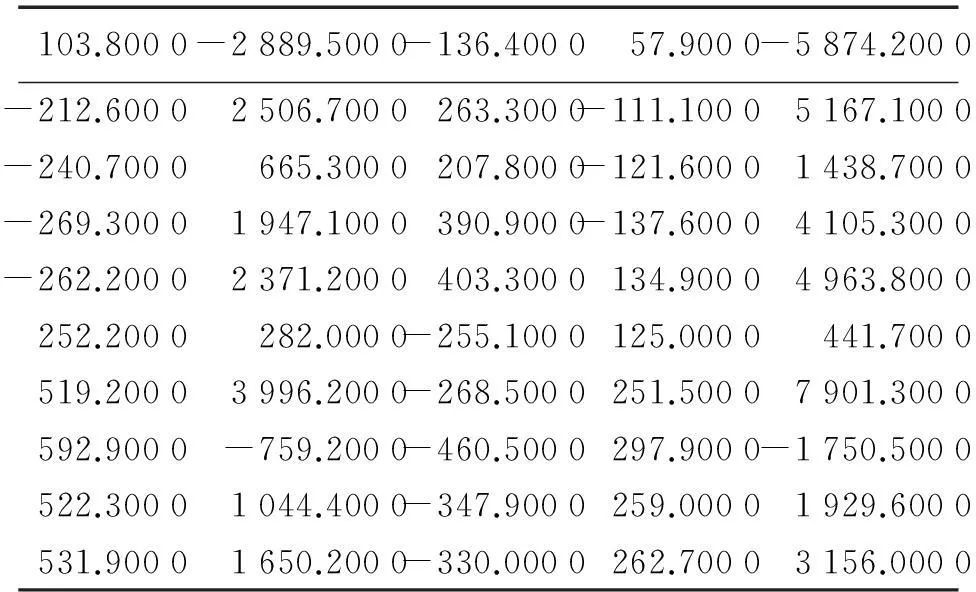
表1　新的病态矩阵

对新的矩阵进行病态处理，分以下几种情况进行讨论：

1) 产生的10个随机误差为0.012 6、0.016 2、-0.014 9、0.016 5、0.005 3、-0.016 1、-0.008 9、0.001 9、0.018 3、0.018 6，将(-0.02,0.02)加入到系数矩阵与未知数的真值的乘积，即作为观测误差，一起作为观测值。

2) 产生10个随机数误差0.031 1、-0.092 9、0.069 8、0.086 8、0.035 7、0.051 5、0.048 6、-0.021 6、0.031 1、-0.065 8，为(-0.1，0.1)。

3) 产生10个随机数误差0.251 3、-0.244 9、0.006 0、0.199 1、0.390 9、0.459 3、0.047 2、-0.361 4、-0.350 7、-0.242 5，为(-0.5,0.5)

由程序编写得到的解见表2。

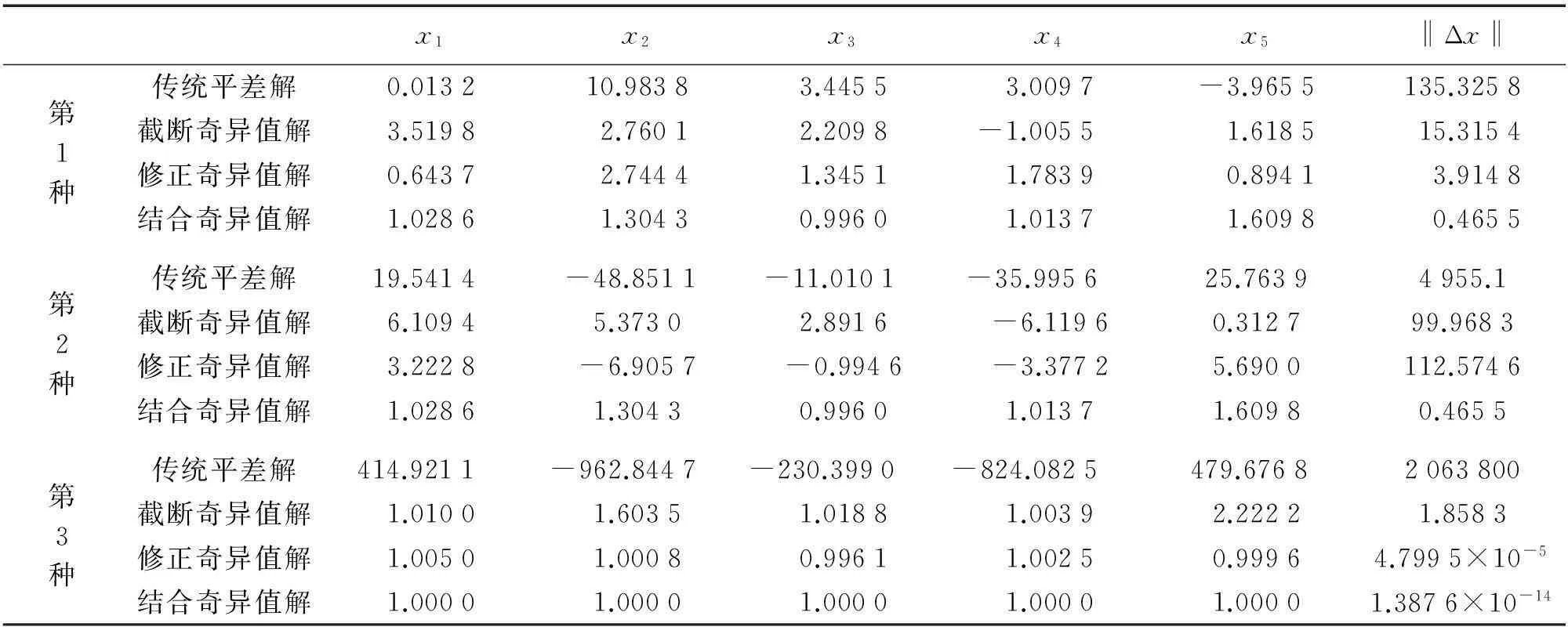
表2　由程序编写得到的解

三、结束语

由Matlab进行程序的编写后[3]，在加入误差较小时，病态矩阵的传统平差解跟真值相差较大，即解的波动较大，符合病态方程的求解条件。同时，截断奇异值后的解和修正奇异值后的解，以及结合二者的解更接近于真值一些，但是结合二者后的解即修

正奇异值截断解比截断、修正的解更接近于真值，也就是微小的扰动对于结合二者后的解法对于未知数的影响较小，即结合二者后的解法抗干扰的能力更强。加入的误差越来越大时，截断、修正奇异值的解抗干扰能力更弱一些，也就是结合二者的解更好一点，适用性更强。总体上来说，都是结合奇异值分解法(截断奇异值分解法和新的修正奇异值分解法、结合二者的分解法)要比传统的最小二乘方法要好，结合二者的分解法即修正奇异值截断法要比截断、修正分解法要好。

参考文献：

[1]卢波. 病态方程的奇异值分解算法与比较[J]. 测绘信息与工程,2011;36(4)：19-22.

[2]王振杰. 测量中不适定问题的正则化解法[M] . 北京: 科学出版社, 2006:86-131.

[3]王振方.基于奇异值分解的拟稳平差法[J].测绘通报,2008(5):30-32.

[4]崔希璋.广义测量平差(新版)[M].北京：测绘出版社，2001.

[5]陈永春.MATLAB语言高级编程[M].北京：清华大学出版社，2004:100-120.

引文格式：徐文，陈义，游为. 奇异值分解法在病态问题中的应用[J].测绘通报，2016(1)：62-63.DOI:10.13474/j.cnki.11-2246.2016.0015.

通信作者：陈义。E-mail: chenyi@tongj.edu.cn

作者简介：徐文(1991—)，男，硕士生，主要研究方向为测量数据处理。E-mail:2890923816@qq.com

收稿日期：2014-11-03

中图分类号：P22

文献标识码：B

文章编号：0494-0911(2016)01-0062-02