唐山地区居民楼楼间距的优化设计

杨柳丛,闫德峰,阎少宏,张静怡,肖同,刘俏

(1.华北理工大学 信息工程学院，河北 唐山 063009；2.华北理工大学 机械工程学院，河北 唐山 063009；3.华北理工大学 数学建模创新实验室，河北 唐山 063009；4.华北理工大学 经济学院，河北 唐山 063009；5.华北理工大学 建筑工程学院，河北 唐山 063009)

唐山地区居民楼楼间距的优化设计

杨柳丛1,闫德峰2,阎少宏3,张静怡4,肖同5,刘俏2

(1.华北理工大学 信息工程学院，河北 唐山 063009；2.华北理工大学 机械工程学院，河北 唐山 063009；3.华北理工大学 数学建模创新实验室，河北 唐山 063009；4.华北理工大学 经济学院，河北 唐山 063009；5.华北理工大学 建筑工程学院，河北 唐山 063009)

楼间距；太阳高度角；数学建模；优化设计

居民楼的合理采光是人们健康生活的基本保障，而开发商通过减小楼间距来谋求更大的经济利益，从而导致居民楼采光问题不容乐观。经调研发现，唐山市市区居民楼楼间距的设计存在严重的不合理现象。依托太阳高度角计算公式，根据唐山市的地理纬度，列出对应的微分方程，从而求出唐山市楼间距优化距离。

0 引言

由于居民楼楼间距变小，靠北一侧的居民楼可能会被靠南一侧的居民楼的影子遮挡，进而影响到北侧低楼层住户的采光。鉴于我国拥有辽阔的土地，从最北边的漠河到最南边的南沙群岛，南北跨越地球纬度达50°，而同一时刻不同纬度地区的太阳高度角是不同的，故不能用统一的标准去衡量不同地区的楼高与楼间距问题。随着现代经济的高速发展，由于开发商过分追求经济效益从而导致楼层过高、楼间距减小，人们日常生活所需光照不足。因此，在建筑设计居民楼时，综合考虑楼间距问题具有非常现实的意义。

在我国强制性标准《城市居住区规划设计规范》中规定，一般普通小区居民住宅楼高比楼间距应满足1：1.2的比例关系。但是由于我国南北跨度较大，南方与北方在同一时期的太阳高度角相差较大，如果用统一的标准去衡量会产生浪费土地的情况，所以应当根据不同地区建立不同的楼间距管理规定。

1 居民楼楼间距优化设计

本研究以唐山市新华联社区居民楼为例，其楼层高度为31层，每层楼的高度为2.7 m，楼高为90 m，而新华联社区相邻两栋楼之间的楼间距为45 m，新华联南侧的楼会遮挡住北侧楼的三分之一高度。

1.1 太阳高度角的建立

若要得到合理的楼间距，则需得知当地的太阳光线与居民楼的夹角，即太阳高度角。对于地球上的某个地点，太阳光的入射方向和地平面之间的夹角为太阳高度角。太阳高度角是指某地太阳光线与通过该地与地心相连的地表切线的夹角[5]，如图1所示，H为太阳高度角，CD为楼高，CE为影长。

根据太阳高度角的公式:

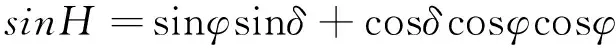
(1)

式中：H为太阳高度角，φ为太阳赤纬，δ为所在地的地球纬度，φ为时角。其中时角的计算公式：

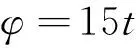
(2)

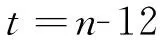
(3)

式(3)中n 为当地的时间,联系式(1)、(2)和(3):

(4)

在式(4)中，只要知道太阳赤纬φ，所在地的地球纬度为δ，时角为φ，就可以对应求出太阳高度角[5]。把当天的时间作为自变量，建立方程时暂且不考虑地球公转对影长的影响，仅考虑地球自转，经查找资料得到赤纬的计算公式为：

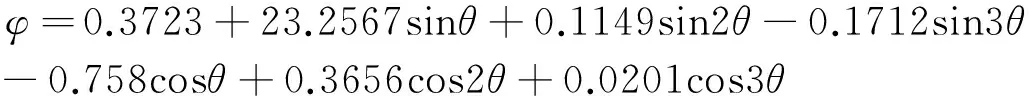
(5)

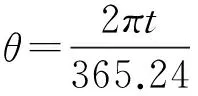
(6)

1.2 最佳楼间距的求解

唐山市所在地理位置为北纬39°，经调研得知，不同居民楼对应的楼层数和楼间距数据如表1所示，唐山市居民楼的平均楼层数为25层，居民楼的楼层高度一般为2.7 m，平均楼高为67.5 m，平均楼间距为40 m，唐山市位于北半球，冬至日太阳高度角最小，所以所选日期为冬至日12月22日，时间为正午12时。

表1 唐山市居民楼的楼高与楼间距

楼间距问题实际是一个影长的问题。其设计的基本原则是前一幢楼产生的影子不应挡住后一幢楼的采光(一般以太阳光线能够照射至后一幢楼的底层为标准)，并且住宅日照标准应符合如下标准：大寒日不小于2 h，冬至日不小于1 h。旧区改造可酌情降低，但不宜低于大寒日的日照1 h的标准。

因为正午太阳高度角最大值，意味着前一幢楼的影子是一天中最短的，所以一般取当地正午时间对应的太阳高度角，此时楼间距能确保一年四季居民楼都能得到所需的采光。因此,一般北半球取冬至日的正午太阳高度角，南半球取夏至日的正午太阳高度角[3]。唐山位于地球的北半球，所用时间为冬至日。实际光照情况如图2所示：

在图2中,正午太阳高度角为H ,平均楼高为h,楼间距为L,计算公式如下:

(7)

由赤纬的求解公式联立得方程组：

联立式中,冬至日时间为12月22日,对应的积日N=355,N0=79.9424,t=275.0576,得出日角为θ=4.7318,并进一步得出太阳赤纬为φ=-23.4366°,将所得结果代入以下方程组:

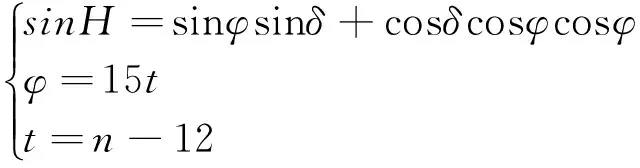
从而得出时角为φ=0,唐山所在地的地球北纬为δ=39°时,计算得出太阳高度角为H=15.9083°,楼间距为L=59.8387m。

2 应用与推广

该项研究建立了太阳高度角、经纬度和时间之间的关系式，并得到太阳高度角与楼高、影长之间的关系。利用这个关系式，可以求得任意城市的居民楼间距的最佳值。该城市若位于北半球，取冬至日时间；若位于南半球，则取夏至日时间，再将该城市的经纬度带入式中，即可求得该城市的太阳高度角，并可进一步根据太阳高度角和当地城市居民楼的平均高度求得该城市居民楼楼间距的最佳值。

3 结论

(1)通过对唐山市区居民楼间距的研究，发现唐山市区的居民楼之间的设计存在很大问题，很多居民楼的楼间距并不符合理论计算结果。

(2)通过对唐山市区的实地调研可知，唐山高层居民楼的平均楼高为67.5 m，但是唐山市区高层居民楼之间的楼间距平均为40 m，因此会遮挡北侧居民楼三分之一的楼高，从而影响楼层低的住户的采光、隐私、通风问题。根据建立的数学模型求解唐山市区最佳楼间距应为59.8 m。

[1] 姜启源.数学模型[M].北京:高等教育出版社,2003.89-160.

[2] 丁丽娟.数值计算方法[M ].北京:北京理工出版社,2007.36-158.

[3] 林晨. 基于日照因素影响下的高密度住区设计研究[D].大连：大连理工大学,2011.

[4] 赵静. 采光通风被挡怎么办 让"环境保护相邻权"为你做主[J]. 环境与生活，2014,15:44-45.

[5] 王国安. 太阳高度角和日出日落时刻太阳方位角一年变化范围的计算[J]. 气象与环境科学,2007,S1:161-164.

[6] A Ekholm,S Fridqvist. A concept of space for building classification, product modelling, and design[J]. Automation in Construction, 2000,93:315-328.

[7] Georg Suter. Structure and spatial consistency of network-based space layouts for Building and product design[J]. Computer-Aided Design,2013,458-9:1108-1127.

[8] 戴立飞. 中小型建筑自然采光设计研究[D].天津：天津大学,2006.

[9] 吴丹.注重楼间距,巧用装饰护"隐私"[J].楼市,2011,08:71-73.

[10] 费云霞,王春顺. 对太阳高度角的了解及其计算方法[J]. 中小企业管理与科技(上半月),2008,01:116-117.

Optimum Design of Space Between Residential Buildings in Tangshan

YANG Liu-cong1, YAN De-feng2, YAN Shao-hong3, ZHANG Jing-yi4,XIAO Tong5,LIU Qiao2

(1.College of Information Engineering, North China University of Science and Technology, Tangshan Hebei 063009, China; 2.College of Mechanical Engineering, North China University of Science and Technology, Tangshan Hebei 063009,China; 3.Mathematical Modeling Innovation Lab, North China University of Science and Technology, Tangshan Hebei 063009, China; 4.College of Economics, North China University of Science and Technology, Tangshan Hebei 063009, China; 5.College of Architectural Engineering, North China University of Science and Technology, Tangshan Hebei 063009,China)

space between two buildings; solar altitude; mathematical modeling; optimum design

Reasonable lighting of residential building is the basic guarantee of people's healthy life, while the property developers to seek for greater economic benefits by reducing the space, thereby leading to residential buildings lighting issues can not be optimistic. The result shows that the design of the space of residential buildings in Tangshan City exists serious unreasonable phenomenon. Relying on the formula of solar altitude, according to the Tangshan geographical latitude, the corresponding differential equations formulated are formulated, and then obtain optimization distance of residential buildings in Tangshan.

2095-2716(2016)02-0129-04

X799.1

A