基于关联规则的区间概念格属性约简模型

徐珺，李明霞

(1.华北理工大学 轻工学院，河北 唐山 063000；2.华北理工大学 理学院，河北 唐山 063009)

基于关联规则的区间概念格属性约简模型

徐珺1，李明霞2

(1.华北理工大学 轻工学院，河北 唐山 063000；2.华北理工大学 理学院，河北 唐山 063009)

区间概念格；属性约简；关联规则；冗余属性

区间概念格的属性约简是在保持形式背景上所有区间概念的上、下界外延集不变的前提下，寻找极小属性子集，该属性子集依然能够完全确定形式背景上的所有区间概念，并基本保持它们之间原有的层次结构关系。根据给定的形式背景构建相应的区间概念，进而得到量化的区间概念，然后依据量化区间概念的上界外延数先查找频繁结点后，再进一步提取强置信度的关联规则，最后根据这些关联规则去掉信息表中的冗余属性，达到约简的目的。经验证，由约简后的信息表得到的格结构层次较约简前变化不大。

在实际生活中，某一对象的各属性之间一般不是相互独立的，统计学方法中就有主成分分析，因子分析法等对多维信息表进行降维处理。由于大数据时代的到来，各种各样的信息表中包含了众多属性，然而对最终的分类影响比较大的可能只占全部属性的一部分，其他的属性可能对最终的分类没有明显的贡献，故称之为冗余属性。去除冗余属性对于构建区间概念格有着重要的意义，不仅能保持较高的分类效率，而且可以使结构变得简单，计算更加容易，利于提高计算速度。

对于概念格属性约简方法的研究，早就有基于属性特征的概念格约简算法[1]，基于差别矩阵及其改进的概念格约简算法[2]，基于粒的概念格约简算法[3]以及基于交可约元的概念格约简算法[4]等，这些算法中有些需要计算繁琐的差别矩阵，有些可能会在时间复杂性和空间复杂性上增加难度。本文则从简单的关联规则挖掘方法[5-6]入手，发现蕴含式中存在的冗余属性可以在保持格结构基本不变的情况下去除，然而这些关联规则都必须在较大支持度和置信度下提取，往往一般经典的概念格很难达成这样的效果，而针对于区间概念格，这种方法得到了很好应用并通过实例验证了其有效性。

1 预备知识

1.1 区间概念相关理论

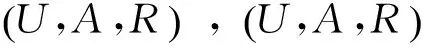
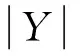
定理2α不变，β趋向于1时，近似精度减小，粗糙度增大。

定理3β不变，α趋向于β时，近似精度接近于1，粗糙度接近于0。

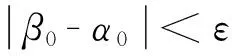
1.2 基于区间概念格的关联规则

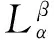
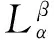
依据区间概念格对应的父子关系(偏序关系)可以进行关联规则的快速挖掘，下一节设计了这样的快速挖掘算法。

与经典概念格不同，区间概念格中的父子概念在频繁性上不具有特定的关系。

定义8关联规则AB对应于区间概念格中的结点二元组(C1,C2)，且C1≥C2，称规则AB由结点二元组(C1,C2)生成。

区间概念中有上下界两个概念外延，可分别提取α-上界关联规则和β-下界关联规则。它们的支持度和置信度计算方法为：

α-上界规则AB：

β-下界规则AB：

定义9对区间关联规则AB，若满足如下2个条件，则被称为强关联规则。

(1)A∪B是频繁项集，Support(AB)≥θ

(2)Conf(AB)≥φ，即≥φ

从区间概念格的角度来看，关联规则可以用内涵之间的蕴含关系来描述，而关联规则本身体现的是相应外延间的近似包含关系。由于区间概念格是内涵和外延在一定比例下的统一，并且节点间的关系也体现了概念间的泛化和例化的关系，因此区间概念格作为概念格的一种特殊形式很适合成为关联规则挖掘的基础性数据结构。对于提取出来的规则往往用户需要的数量较少，易于理解，更能反映真实情况的关联规则。

1.3 基于量化区间概念格的关联规则提取算法

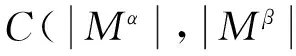
根据最小支持度计数，在量化区间概念格中寻找外延个数大于最小支持度计数的概念，其内涵就是频繁项集。

算法：基于量化区间概念格的关联规则提取算法；

输入：形式背景M，区间参数[α,β]，最小支持度阈值θ，最小置信度阈值φ；

输出：关联规则。

步骤：

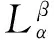
Step3，根据最小支持度阈值θ，直接在量化区间概念结点中选取上、下界频繁概念结点，从而去掉上、下界非频繁概念结点，得到满足支持度的区间量化概念格结构，为进一步提取关联规则奠定基础；

Step4，根据定义4、6、8、9以及给定的最小置信度阈值φ，提取相应的关联规则[11]，概念格中结点产生的规则依赖于它的双亲结点。首先遍历该结点的双亲结点，然后根据外延计数值计算是否满足最小置信度，如果满足，则对该节点生成所有非冗余规则。

2 基于关联规则的区间概念格属性约简理论及算法

根据第1.3节提取出的关联规则，进行去冗余属性。在这之前，将介绍相关的理论基础。

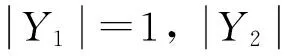
由定理4 可知，区间参数的设定会导致当概念内涵增加时，区间概念的上、下界外延不一定呈现缩减趋势，不难说明，这样的规律会间接导致在区间概念格中能够查找到高支持度的频繁节点。同时关联规则的置信度对区间概念格属性约简的影响也是不容忽视的，当然当最小置信度达到1时，则可以认定规则AB是完全可以信任的，并且这样的规则在生产生活中的应用价值较高。

简要算法：基于关联规则的区间概念格属性约简算法；

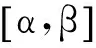
输出：新的形式背景M'。

步骤：

Step1，根据给定的形式背景M和区间参数

Step3，根据最小支持度阈值θ，直接在量化区间概念结点中选取上、下界频繁概念结点，从而去掉上、下界非频繁概念结点，得到满足支持度的区间量化概念格结构，为进一步提取关联规则奠定基础；(在这里最小支持度阈值一般取1)

Step4，变置信度观察格结构层次以及规则数量精度的变化：

(1)初始化最小置信度阈值φ0=1；

(2)根据之前选定的频繁概念节点，计算是否满足φ0，如果满足则根据频繁项集提取规则，转(4)，否则转(3)；

(3)φ0-0.1，转(2)；

(4)根据提取出的关联规则，去掉冗余属性，例如：AB，去掉属性B；

Step5，根据去掉冗余属性的形式背景，构建区间概念格，观察格的层次结构。

3 实例验证

在选购商品时，往往会被一些商品众多的属性妨碍，使得人们不能在短时间做出准确的选择；或是商家在面对不同商品的大量属性时很难做出快速有效地分类，这些现象都会降低人们生活的质量，因此在不改变商品重要属性的同时去除商品冗余属性是十分重要的。

在下面给定的形式背景中，包含10种电子产品及8个条件属性，这些属性之间存在并不是相互独立的，有些属性是冗余的，研究目标是经约简后可以得到这些电子产品的区分属性并更易于分类，同时不改变所构建的区间概念格的层次结构。这些电子产品的条件属性分别是：外形美观、机身耐用、性能高端、待机时长、音质良好、价位较高、像素清晰、配件齐全，如表1所示。

表1 电子产品信息表

根据第1.3节的算法，首先确定区间参数为[0.5,1]，之前已经验证过当区间参数α=0.5时，区间概念格结构最为稳定，并且在此基础上提取出的一般关联规则数目和精度都是很可观的；最小支持度阈值为1，区间概念格本身就具有描述不确定性事物的特性，因此支持度不为1时，可能会造成不准确，甚至是错误的信息。然后根据给定的区间参数构建区间概念，下面列举部分区间概念，如表2所示。

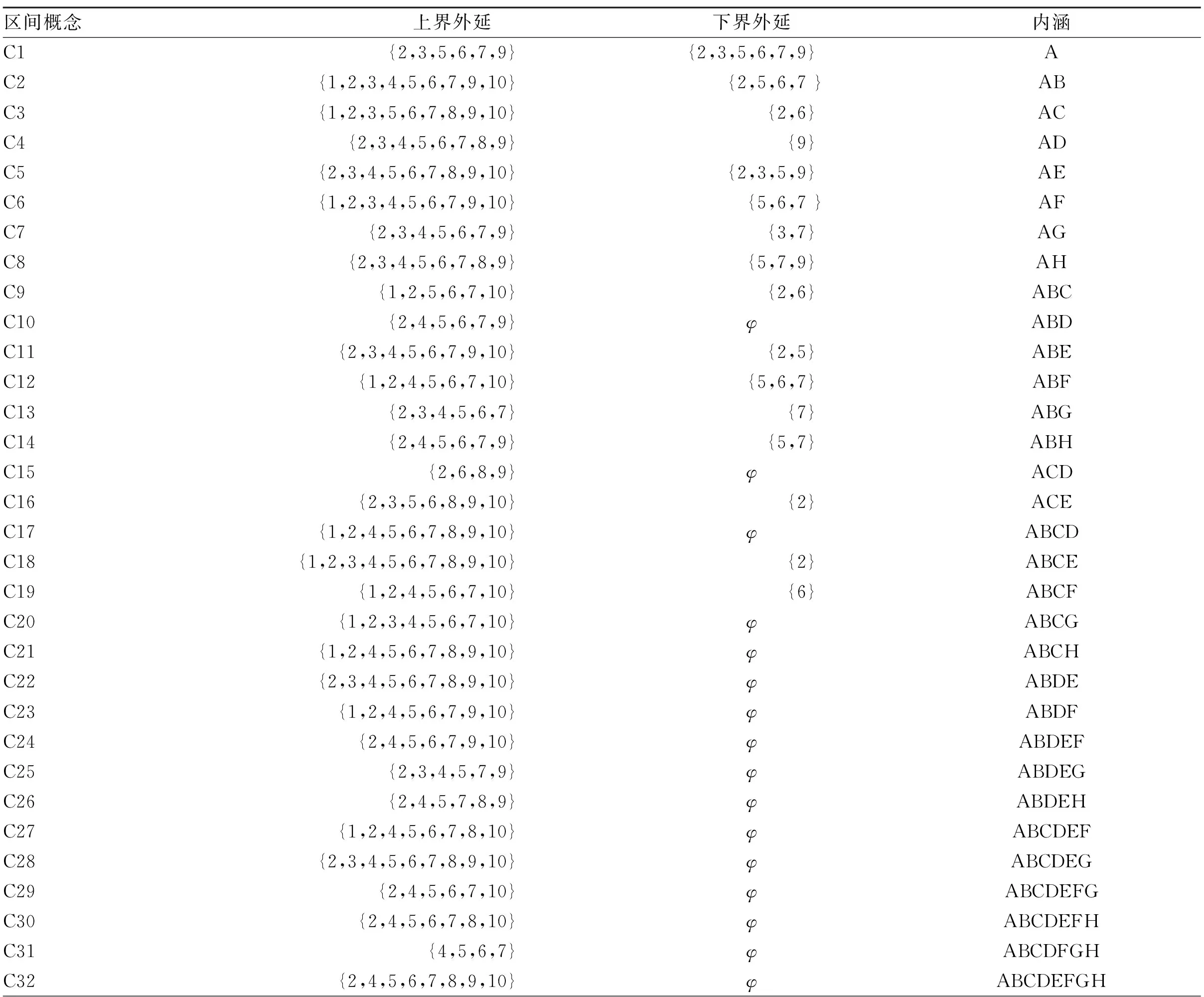
表2 部分区间概念表

部分区间概念格结构如图1所示。

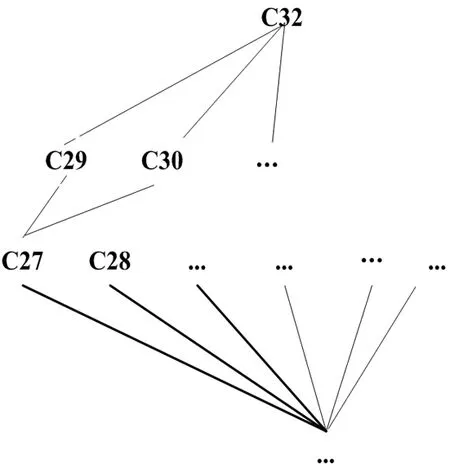
图1 部分区间概念格

转化成量化区间概念的形式，查找频繁概念节点，满足要求的节点为：(10,*,EF)，(10,*,ABCE),，(10,*,ACEF) (*表示下界外延基数不计，为了方便，区间参数β=1，外延基数极少，只研究上界关联规则，符合区间概念格约简的目的不影响约简结构)，由此根据父子节点的偏序关系挖掘出相应的关联规则为EFAC。

根据第1.3节的简易算法的结果发现：EFAC，该关联规则的置信度为1，符合要求，可以去掉冗余属性AC，更新后的信息表为表3。

表3 去冗余属性后信息表

经检验，发现由此构建的区间概念格层次结构没有发生根本变化，故该约简具有效性。

4 结论

(1)概念格约简算法并不是唯一的，同时不同的形式背景会有相应有不同的约简算法，本文主要考虑的是无决策形式背景下的区间概念格属性约简问题，侧重于各个条件属性之间的关联性。

(2)在区间概念格这种特殊新颖的结构下进行关联规则的挖掘，验证发现这种约简方法的可行性，但是该方法是否可以应用于一般经典的概念格属性约简问题还有待于具体问题具体分析。

[1] 王霞,张文修. 概念格的属性约简与属性特征[J]. 计算机工程与应用. 2008,44(12):1-4.

[2] 刘文军,谷云东,冯艳宾,等. 基于可辨识矩阵和逻辑运算的属性约简算法的改进[J].模式识别与人工智能. 2004,3(17):119-123.

[3] 叶东毅,廖建坤. 基于二进制粒子群优化的一个最小属性约简算法[J].模式识别与人工智能. 2007,20(3):296-300.

[4] 林培榕,张其森,李进金.基于交可约等价类的概念格属性约简[J].模式识别与人工智能. 2010,23(5):721-726.

[5] 张学斌,丁晓明. 一种基于关联规则的属性约简算法[J]. 西南师范大学学报(自然科学版). 2005,30(3):441-443.

[6] 杨明,吉根林,姜志峰,等.一种基于关联规则的最小属性约简模型[J].计算机科学. 2003,30(10):274-277.

[7] 刘保相, 张春英. 一种新的概念格结构—区间概念格[J].计算机科学, 2012, 39(8):273-277.

[8] 王德兴. 基于概念格模型关联规则挖掘的关键问题研究[D]. 合肥: 合肥工业大学,2006.

[9] 胡学钢. 从数据库中提取知识的模型研究[D].合肥：合肥工业大学, 2000.

[10] ZHANG C Y, WANG L Y, LIU B X. An effective interval concept lattice construction algorithm [J]. ICIC Express Letters, Part B: Applications, 2014, 12:1573-1578.

[11] 王立亚. 区间概念格高效建格算法研究与应用[D]. 唐山: 华北理工大学, 2014.

[12] 王晓龙. 基于关联规则属性约简的树增广朴素贝叶斯分类器及应用[D]. 长春: 吉林大学硕士论文, 2014.

[13] 阎红灿, 王会芳, 刘保相. 区间概念格的结构特性与应用[J]. 微型机与应用, 201433(9):98-100.

Model of Attribute Reduction about Interval Concept Lattice Based on Association Rules

XU Jun1, LI Ming-xia2

(1.Qinggong College, North China University of Science and Technology, Tangshan Hebei 063000, China; 2.College of Science, North China University of Science and Technology, Tangshan Hebei 063009, China)

interval concept lattice; attribute reduction; association rule; redundant attribute

The attribute reduction of interval concept lattice is based on the invariable upper and lower extension in formal context to find minimal attribute subsets, which can also entirely define all interval concepts on the formal context and basically maintain the original hierarchical structure between them. According to the given formal context, the corresponding interval concepts are constructed, and then quantitative interval concepts are obtained. We can find frequent nodes according to the number of upper extension in quantitative interval concepts, and then extract the association rules with strong confidence. Finally, according to these association rules we can remove redundant attributes in the information table and achieve the result of reduction. It has been proved that lattice structures from reduced information table little change than before.

2095-2716(2016)02-0051-07

TP301.6

A