多情景下应急物流多源选址的优化及实现

孙立波,赵志勇,纪楠

(1.华北理工大学 电气工程学院，河北 唐山 063009；2.华北理工大学 信息工程学院，河北 唐山 063009；3.华北理工大学 理学院，河北 唐山 063009)

多情景下应急物流多源选址的优化及实现

孙立波1,赵志勇2,纪楠3

(1.华北理工大学 电气工程学院，河北 唐山 063009；2.华北理工大学 信息工程学院，河北 唐山 063009；3.华北理工大学 理学院，河北 唐山 063009)

应急物流；多情景；多源选址；时效性；两步式启发算法

应急物流配送中心的选址是应急物流系统设计的关键性问题，综合考虑了不同类型大规模突发事件造成的应急物资需求不确定性，构建了带时效性约束的多情景下多配送源选址模型，结合前人的研究，基于联系数理论，使模型转换为可求解的确定性模型，给出了交替选址迭代算法用于求解配送中心分配矩阵。最后，设计了两步式启发式算法，并通过算例对模型进行了模拟分析，验证了算法的有效性。

我国是一个自然灾害频发的国家，各种各样的自然灾害，如地震、台风、水灾、旱灾等，这些突发事件往往是大范围的，从曾经的南方冰冻灾害、禽流感，再到南非的埃博拉病毒，它们给我国乃至世界人民的生命与财产造成了重大的损失。应急物流的研究对这些突发灾害中物资配送策略的制定有着重要的意义。应急物流是指以提供重大自然灾害、突发性公共卫生事件及公共安全事件等突发性事件所需应急物资为目的，以追求时间效益最大化和灾害损失最小化为目标的特种物流活动[1]。然而，应急物流与普通物流存在明显的不同，应急物流在许多情况下只能通过物流效率来实现物流效益，因为它更强调时效性。在应急物流的研究中，应急物资的配送中心选址问题至关重要，它直接关系到应急物资配送系统的优劣。本文在分析了应急物流网络布局的发展现状及其特性的基础上，就怎样更好地构建应急物流配送中心模型，以达到在最短的时间内准确地将救灾物资紧急配送到灾区，获得最大化救灾效益问题进行了深入的研究。

目前，随着我国突发事件发生频率的增加以及国家的重视，针对基于应急物流的连续型选址建模与算法研究已经逐步展开，例如王保华等人构建了不确定环境下物流中心选址的鲁棒优化模型；李利华等人建立了基于重心法的物流网络区间节点决策模型；龚延成等人应用启发式算法求解了带时效性约束的多源选址问题，分析了物流配送的时效性问题；商丽媛等人构建了不确定情境下的应急物流配送中心选址模型，并给出了改进的粒子群免疫启发式算法。前人的诸多研究各有独到之处，但是选址往往要考虑多方面的因素，例如，突发事件类型的不同会造成需求点需求量的不同，不同突发灾害下物资配送的时效性等，然而前人很少有结合这些方面进行综合建模研究，如果可以在模型中较为全面地考虑这些，便可以使选址方案的制定更加符合实际，从而实现选址策略的进一步优化，这便是该项研究的主要工作。

1 应急物流选址策略探究

1.1 多情景

灾害的发生往往是突发性的，灾害的类型和等级也有所不同，因此应该考虑不同情景下的突发事件对需求点物资需求量的影响，前人常常是在某一确定类型的灾害背景下去建模分析，以最小周转量为目标函数，这样的考虑是不全面的，某一地区灾害发生的情景具有不确定性，如果能通过历史数据计算不同情景下灾害发生的概率，最终建立基于概率的综合最小周转量为目标函数的选址模型，那就会更加符合实际。

1.2 需求量的不确定性

要制定更加符合实际的选址策略，则对灾区的应急物资需求量的考虑必不可少。规划配送中心位置必须认识到，某地区突发事件出现的情景不同会造成供需关系不明确，我们往往需要先对灾区的供需状况进行评估，确定供需是否平衡，供给能否满足灾区需求，因此，我们在前期配送中心选址规划中应该考虑到各需求点需求量的不确定性。

1.3 时效性

应急物流具有时效性、弱经济性和情景的不确定性等特点，突发性和不确定性要求应急物流必须在最短的时间内完成，实现高效率[2]。时效性是任何应急物流选址必须考虑的因素，全面地考虑时效性，对提高救援效率、降低救援成本、提高应急物资配送系统的救援能力等方面都起到了至关重要的作用。

2 多情景下应急物流多配送点中心选址模型的构建

本文主要研究在发生大规模突发事件情况下配送中心选址问题的优化。综合考虑不同突发事件情景的发生概率及该情景下需求量的不确定性，将不确定需求用区间灰数[3]表示，多情景下多配送中心选址问题可描述如下：

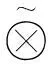
设需要建立p个配送中心，其为q个需求点提供物资服务。设第i个物资配送中心的地址坐标为(Xi,Yi),i=1,2,...,p,第j个需求点坐标为(xj,yj)，j=1,2,...,q，用ps表示某地区第s种突发事件情景出现的概率，H表示情景的集合，s∈H，将第s情景下第j需求点的需求量用⊗sj来表示，其表示第j需求点的动态变化的需求量，以不同情景下综合的平均周转量最小作为目标函数。

(1)应急物资配送方案矩阵F的确定：

其中，lij是一个二进制数，当第i配送中心为第j需求点提供配送服务时，则lij=1；否则lij=0。配送方案矩阵F可以初步将q个需求点分配给p个配送中心。然后通过迭代算法求出配送中心的初步位置。当确定了配送中心的初步位置后，便可以将多配送中心选址转换为单配送中心选址问题，而约束变量：最大允许配送距离Dj的求解

其中，Lij表示分配到每一个配送中心周围任意2个需求点间的最大距离

(2)最终的选址模型为：

目标函数：

(1)

约束条件：

(2)

(3)

(4)

3 模型的求解

3.1 区间灰数转化为联系数

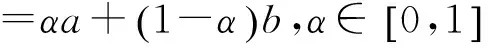
3.2 两步式启发算法

由于模型更加符合实际，求解也变得更加复杂，在此借鉴了文献[5]的两步式启发式算法上对其进行了修改，得到了适合对模型求解的启发式算法。在此仅给出算法核心思想，算法核心思想是：

(1)将含区间灰数参数的模型转化为确定性模型，再通过迭代算法，先不考虑时效性约束(2)式，用目标函数(1)式和约束条件(3)式进行选址计算,确定分配矩阵F；

(2)考虑时效性约束条件(2)式，转化为单个连续性选址问题，用MATLAB优化函数分别对每个物资配送中心进行选址计算，最终确定优化的选址方案。

4 算例的仿真模拟

现有某应急物流区域，需要建立2个物资配送中心，范围为(0，0)～(100，100)，该区域内有10个需求点，有3种不同情景(3种突发事件)，在该地区出现概率分别为p1=0.7，p2=0.25和p3=0.05，各需求点在不同情景下的需求量区间为区间灰数，如表1所示，试利用本文的模型确定2个物资配送中心坐标，使得在满足时效性约束的前提下，多情景下的物资配送的综合平均周转量最小。

表1 需求点在3种情景下的需求量区间及坐标位置

具体求解步骤：

P1P2P3P4P5P6P7P8～1j18.7514.1228.8021.9118.1612.2116.8015.75～2j36.3226.2554.8648.0042.7824.0032.9429.87～3j63.7558.3388.8974.7266.0456.6054.6051.93

(2)服务配送方案矩阵S的确定单配送中心选址重心法：对于第i配送中心，用最小二乘法可以推导出迭代公式[6]，则迭代横纵坐标为

(5)

从而可以得到第m次迭代运算后需求点j到配送中心的距离：

(6)

迭代过程如下：

S1：初始化配送方案，将需求点P1～P8随机分成(P1，P3，P6，P7)和(P2，P4，P5，P8)两组，每一组有一个配送中心负责送货，初步确定多源选址服务分配矩阵F0,对应的初始化分配矩阵：

S2:各个配送中心坐标计算。按照初始化配送方案F,将每个配送中心坐标按(5)和(6)式迭代运算,初步计算出这2个配送中心的地址坐标[Xi,Yi],i=1,2。求出2个配送中心的地址坐标:[X1,Y1]=(62.04,56.42),[X2,Y2]=(56.672,42.83)

S3：调整初始化配送方案。用公式：

(7)

计算第j需求点分别到配送中心i的运输中转量并将计算结果列表。

S4：仔细检查列表，将不合适的配送方式利用lij=0/lij=1来调整，按调整结果确定新的分配矩阵F，并转S2。最后使得所有需求点都能划归到具有最低运输周转量的那个配送中心负责送货，则矩阵F为最佳分配方案,算法终止。最终得到的迭代后的选址坐标为[X1,Y1]=(56.0465,82.1233)，[X2,Y2]=(52.1122,18.2064)；多源选址服务分配矩阵F为：

原则上讲，到这一步已经求出了最佳的服务分配方案和物资配送中心的地理坐标，但没有考虑时效性对目标的影响，所以要求解在(2)式约束下该模型的最优解。

(3)下面用基于MATLAB函数的选址优化算法求解调整后的选址坐标。

在确定最佳分配矩阵F后，多配送中心连续选址问题就可以分解为在各个集合中以一个配送中心为目标的单源选址问题，设第i(针对该问题，这里的i取值为1,2,3)个配送中心所服务的需求点的集合为{1，2，3，...，k}，然后带时效性约束的单源选址模型就可以简化为：

目标函数：

(8)

约束条件为：

(9)

上述模型是一个有约束非线形规划的求最小值问题。 MATLAB 优化工具箱中fmincon()函数是求解多变量有约束非线形函数极小值的函数，适合于求解这个带时效性约束的物流配送中心选址模型。运用MATLAB的求解可以得出选址结果为：[X1,Y1]=(60.37,85.11)，[X2,Y2]=(42.00,25.00)，总周转量为3900。

图1为选址结果示意图，虚线表示不考虑时效性约束的选址方案，实线表示考虑时效性约束的方案。

图1 选址分配结果示意图

5 结论

(1)构建了一个有效的多配送中心选址模型，使其具有了一定的通用性，考虑因素较全面，有助于提高应急物资选址的效率，并且将前人的求解算法进行了优化，开发出两步式启发式算法用于模型的求解。

(2)研究成果不仅可以为决策者提供重要的理论参考，也可以为从事疫苗防疫、血液供应、军事后勤、重大灾害等突发事件下应急物流网络布局优化方面的研究人员提供新的思路。

[1] 林敬松.地震灾害应急物流的策略及发展方向分析[J].交通企业管理,2008,11(11):58-59.

[2] SHE J B. Challenges of emergency logistics management [J].Transportation Research Part E: Logistics and Transportation Review, 2007, 43(6):655-659.

[3] 刘思峰,党耀国,方志耕. 灰色系统理论及其应用[M]. 北京: 科学出版社, 2010.

[4] 姜启源,谢金星,叶俊. 数学模型(第三版)[M]. 北京: 高等教育出版社，2003.

[5] 赵克. 二元联系数的理论基础与基本算法及在人工智能中的应用[J]. 智能系统学报,2008,3(6):476-486.

[6] 龚延成,郭晓汾,蔡团结,等.物流配送点选址模型及其算法研究[J].中国公路学报,2003,16(02):124-126.

[7] 商丽媛,谭清美.不确定应急物流中心选址模型及算法研究[J].计算机应用研究,2013,30(12):3603-3605.

Optimization and Implementation of Multisource Site Selection for Emergency Logistics with Multiple Scenarios

SUN Li-bo1, ZHAO Zhi-yong2, JI Nan3

(1.College of Electrical Engineering, North China University of Science and Technology, Tangshan Hebei 063009, China; 2.College of Information Engineering, North China University of Science and Technology, Tangshan Hebei 063009, China; 3.College of Science, North China University of Science and Technology, Tangshan Hebei 063009,China)

emergency logistics; multiple scenarios; multisource site selection; timeliness; two-step heuristic algorithm

Emergency logistics multisource site selection is a critical question of the design on emergency logistic system. In this paper, considering the demand uncertainty caused by the different types of mass incidents, a two-step heuristic algorithm for the constructed model was designed, which is aimed at solving the multisource site selection problems with the uncertain demand and timeliness under different scenarios considered. Based on the previous research, the paper represented the uncertain demand by interval gray number and transformed it to connection number based on the connection number theory because of the constructed objective function containing interval gray number. The model was changed to a determined model, using the improved iterative algorithm to compute the initial distribution matrix. In addition, an example was given to demonstrate the two-step heuristic algorithm. And the result indicates that it is an efficient algorithm.

2095-2716(2016)02-0111-06

U116.2

A