基于MOF算法改进的标量乘算法研究

袁 勇，唐 刚，陈辉焱，万宗杰，张德馨

(1.西安电子科技大学，陕西 西安 710071；2.北京电子科技学院，北京 100070；3.中国软件评测中心，北京 100044)

基于MOF算法改进的标量乘算法研究

袁 勇1,2,3，唐 刚3，陈辉焱2，万宗杰2，张德馨3

(1.西安电子科技大学，陕西 西安 710071；2.北京电子科技学院，北京 100070；3.中国软件评测中心，北京 100044)

标量乘运算是椭圆曲线密码方案中最耗费时间的运算，因此标量乘的运算速度决定了椭圆曲线密码方案的执行速度。为了提高标量乘的执行速度，人们提出了很多方案，如NAF、MOF等。在研究大量标量乘算法的基础上，提出了一种基于MOF算法的改进型ZLMOF算法。改进的算法与原算法相比，在汉明重基本保持不变的前提下，比特串长度上降到了最低，从而进一步减少了点加运算的次数。然后结合滑动窗口算法提出了一种比NAF—滑动窗口算法更加高效的ZLMOF—滑动窗口算法，ZLMOF—滑动窗口算法比NAF—滑动窗口算法需要更少的点加运算次数。又结合Shamir算法，提出了一种比Shamir—NAF算法更加高效的Shamir—ZLMOF多标量乘算法。Shamir—ZLMOF多标量乘算法比Shamir—NAF算法需要更少的点加运算次数。

标量乘；ZLMOF算法；ZLMOF—滑动窗口算法；Shamir—ZLMOF算法；椭圆曲线

0 引 言

公钥密钥的概念由W.Diffie和M.Hellman[1]提出。R.Rivst、A.Shamir和L.Adleman提出了第一种实用的公钥密码算法—RSA算法[2]。N.Koblitz[3]和V.Miller[4]提出了椭圆曲线密码体制。ECC与RSA、DSA相比，具有更高的单比特安全性,因此ECC的密钥尺寸和系统参数较小。除此之外，在对短消息进行加解密时，ECC带宽要求比RSA和DSA低得多。因此ECC在现在保密通信中，特别是在密码芯片、智能卡和移动通信终端设备中的优势越来越明显。所以对ECC进行研究具有十分重要的实际意义。

在椭圆曲线密码体制中，最耗费时间的运算就是标量乘运算。因此标量乘运算的速度就决定了密码方案的运算速度。为了满足密码方案的需要，已经提出了很多标量乘算法，如二进制标量乘算法[5]、DR标量乘算法[6]、NAF标量乘算法[6]、MOF标量乘算法[7]、补数标量乘算法[8]、固定窗口算法[9]和滑动窗口算法[10]等等。文中主要针对MOF算法进行研究，针对MOF算法变换形式进行变换时会出现汉明重不但不会降低反而会增加的现象，提出了ZLMOF变换生成算法，紧接着利用连续倍点运算性质提出了ZLMOF算法。在ZLMOF算法的基础上，利用滑动窗口技术提出了ZLMOF—滑动窗口算法。通过利用预计算进一步提高计算效率。由于ZLMOF表示形式相比NAF表示形式不但在大多数情况下比特串的长度要短，而且0更加集中。因此ZLMOF—滑动窗口算法的计算效率比NAF—滑动窗口算法要高。由于在密码方案中，很多时候会用到多标量乘运算，因此人们提出了直接算法、Shamir算法、Shamir—NAF算法和JSF算法等等[11-12]。文中结合Shamir算法和ZLMOF算法，提出了一种比Shamir—NAF算法更加高效的Shamir—ZLMOF算法。

1 MOF算法

MOF算法原理:对任一标量k，可以表示成形如MOF(k)=(2k)2-(k)2的形式(MutualOppositeForm)。

Okeya在文献[7]中进一步指出标量k的MOF表示形式具有以下性质:

(1)相邻的非零比特的符号是相反的。

具体MOF表示生成算法如下：

算法1：MOF算法。

输入：非零n比特二进制串k=kn-1kn-2…k1k0；

输出：k的MOF形式mkn-1mkn-2…mk1mk0

1)mkn=kn-1。

2)i从n-1到0重复执行。

(1)mki=ki-1-ki；

(2)mk0=-k0。

3)返回mknmkn-1…mk1mk0。

算法2：MOF的点乘算法。

输出：Q=kP。

1)利用MOF表示生成算法计算k的MOF形式。

2)Q=。

3)对于i从l到0，重复执行

(1)Q=2Q；

(2)若ki=1，则Q=Q+P；

(3)若ki=-1，则Q=Q-P。

4)返回Q。

冬春季温室、塑料大棚等设施内栽培甜瓜时，其播种期应在定植前30～35天播种；露地栽培甜瓜时，其播种期应晚霜前25～30天前播种。

下面通过一个实例来进行说明：

例1：k=15。

汉明重为4。

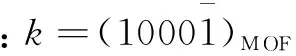
汉明重为2。

通过例1可以发现标量k的MOF表示比起二进制表示的汉明重减少了一半。下面再来看一个例子。

例2：k=42。

汉明重为3。

汉明重为6。

通过例2可以发现标量k的MOF表示形式的汉明重非但没有比二进制的表示形式减少，反而扩大了一倍。

通过上面两个例子可以发现,标量k的MOF表示并非对任意的标量k都可以起到降低汉明重的作用，有时甚至会极大地增加汉明重。除此之外，还可以发现，即使标量k的MOF表示形式并未造成汉明重的增加，但是比特串的长度却增加了，这无疑就增加了一次倍点运算。

为了解决上面的问题，利用左移变换的性质进一步优化，从而将标量k的带符号的二进制表示形式的汉明重降到最低，比特串的长度降到最短，0和1更加集中。将这种新的算法称为ZLMOF算法。下面具体来看一下基于MOF算法改进的标量乘算法。

2 ZLMOF算法

2.1 ZLMOF算法介绍

算法3：ZLMOF算法。

输入：非零n比特二进制串k=kn-1kn-2…k1k0；

输出：k的ZLMOF形式。

1)利用算法1计算k的MOF形式mknmkn-2…mk1mk0。

2)un+1=0。

3)i从0到n重复执行。

(1)当mkimki+1=-1:

②否则，ui=1，ui+1=0，i=i+2，执行3)。

(2)否则，ui=mki，i=i+1，执行3)。

4)输出k的LMOF表示形式。

5)i从n-1到2重复执行：

(1)若uiui-2=-1且ui-1=0：

①若ui=1，则vi=0，vi-1=1，vi-2=1，i=i+3，执行5)；

(2)否则，vi=ui，i=i+1，执行5)。

6)若u2u0≠-1或u1≠0，则v2=u2，v1=u1，v0=u0

7)输出k的ZLMOF。

下面通过具体实例来进行说明。

例3：k=(1100111011101010)，二进制表示的汉明重为10。

k的MOF表示形式为:

此时汉明重为10。

k的NAF表示形式为：

k的ZLMOF表示形式为7。

第一轮变换MOF：

此时汉明重为7。

例3再一次验证了MOF表示形式有时不但起不到降低汉明重的作用,还会增加汉明重。通过例3可以看出，ZLMOF表示形式的汉明重降到了NAF的水平，达到了最低。除此之外，ZLMOF表示形式的比特长度比起NAF形式要短，这样就降低了倍点运算的次数。除此之外，在ZLMOF表示形式中0更加集中，这样便可以通过连续倍点运算进一步提高倍点运算的效率。

算法4:ZLMOF计算点乘算法。

输入：非零n比特二进制串k=kn-1kn-2…k1k0；

输出：标量乘kP的值。

1)用算法3计算k的ZLMOF形式。

2)Q=，w=0。

3)对于i从n-1到0，重复执行：

(1)当ki=0，则w=w+1，i=i+1，执行3)；

(2)Q=2wQ，w=0；

(3)若ki=1，则Q=Q+P；

4)i=i+1。

5)返回Q。

通过算法4可以发现，由于ZLMOF具有较短的比特长度，因此它的倍点运算次数比NAF大多数情况下要少。除此之外，在ZLMOF的点乘运算中，采用了连续被点运算。因此，即使在点加和倍点运算次数相同的情况下，速度也会明显提高。

2.2 ZLMOF算法性能分析

下面随机选取9个随机k值直观地分析一下几种算法表示形式的汉明重及比特长度的大小。

k的取值见表1。

表1 9个k的取值

对表1中的标量k分别进行二进制表示、NAF表示、MOF表示和ZLMOF表示，然后对9个k值在不同表示形式下的汉明重和比特长度进行了计算，具体结果见表2和表3。

表2 9个k值不同表示形式下的汉明重

表3 9个k值不同表示形式下的比特长度

通过表2和表3可以发现，MOF表示形式有时不但起不到降低汉明重的作用，甚至还会造成汉明重的增加。在ZLMOF表示形式中汉明重不但与NAF表示形式的汉明重相同，而且在大多数情况下比特串的长度更加短，从而降低了倍点运算次数。

下面通过计算复杂度进一步分析。

表4是二进制算法、NAF算法和ZLMOF算法的计算复杂性比较。

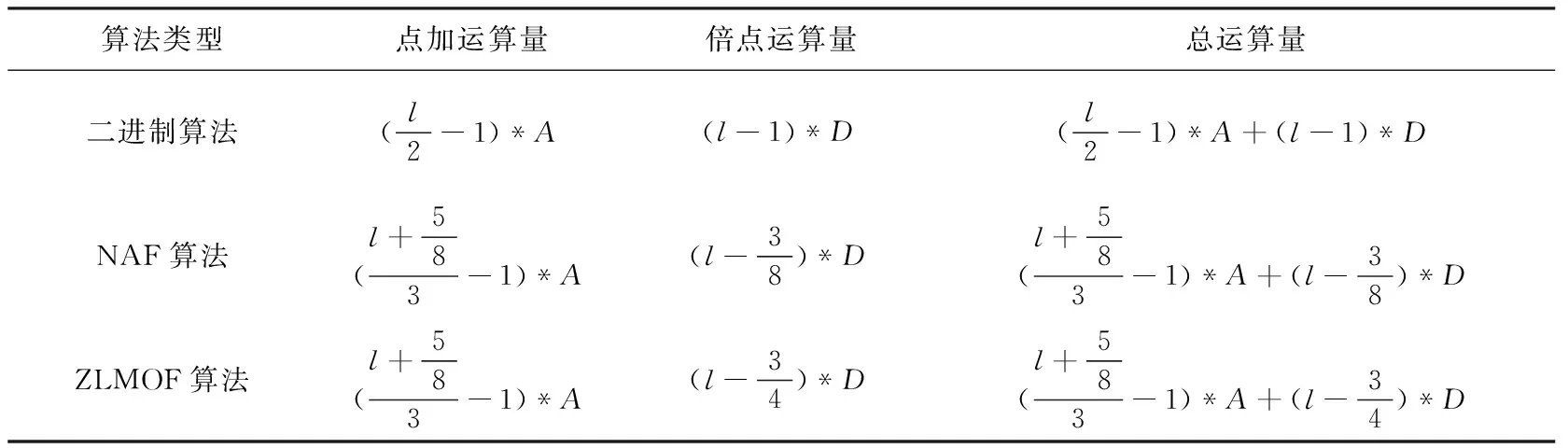
表4 三种算法的主计算量理论分析

通过表4的计算复杂性分析，可以发现：ZLMOF算法尽管倍点运算次数有时会比NAF算法要多1，但是整体的点加运算却比二进制算法明显要少。ZLMOF算法与NAF算法相比，点加次数相同但是整体倍点运算次数却要少。同时ZLMOF的点乘算法中采用了连续倍点运算，因此ZLMOF算法的计算效率比NAF算法的计算效率高。即使NAF算法也采用连续倍点运算，但由于ZLMOF表示形式中0更加集中，因此ZLMOF连续倍点的执行效率也会更高。

3 ZLMOF—滑动窗口算法

3.1 ZLMOF—滑动窗口算法介绍

将滑动窗口算法与文中设计的ZLMOF算法相结合，提出了一种比NAF—滑动窗口算法更加高效的ZLMOF—滑动窗口算法。具体的算法流程如下：

算法5：ZLMOF—滑动窗口算法。

输入：窗口宽度为w，正整数k,P∈E(Fq)；

输出：Q=kP。

2)对于u∈{1,3,…,2w-1+2w-2+2w-3-1}，计算Pu=uP。

3)Q=∞,i=l-1。

4)当i≥0时，重复执行：

(1)若ki=0，则t=1,u=0;

(3)Q=2tQ;

(4)若u>0，则Q=Q+Pu;

(5)否则，Q=Q-Pu;

(6)i=i-t。

5)返回Q。

在算法5中，采用滑动窗口技术，通过预计算，以空间换时间，提高运算效率。

3.2 ZLMOF—滑动窗口算法性能分析

表5 两种算法计算复杂度比较

由于ZLMOF表示形式的0和1更加集中，因此ZLMOF—滑动窗口算法在计算过程中的实际点加次数比理论值要少，因此ZLMOF—滑动窗口算法的实际计算速度比起NAF—滑动窗口算法要快很多。

4 Shamir-ZLMOF算法

4.1 Shamir-ZLMOF算法介绍

将Shamir算法与文中设计的ZLMOF算法相结合，提出了一种比Shamir-NAF算法更加高效的Shamir-ZLMOF算法。具体的算法流程如下：

算法6：ZLMOF—滑动窗口算法。

输入：k1,…,km∈Fq，P1,…,Pm∈E(Fq)；

输出：k1P1+k2P2+…+kmPm。

1)预计算。

(2)计算并存储：

Qa=(P1,P2,…,Pm)·(i1,i2,…,im)T

2)主计算。

(1)将标量k进行ZLMOF表示：

ki=(ki,l-1,…,ki,1,ki,0)ZLMOF

(3)Q=，j=l-1，w=0。

(4)当j从l-1到0，重复执行：

①Q=2Q；

②如果bj≠0，则Q=Q+Qa(Qa为与bj相同的a对应的Qa值)。

(5)返回Q。

在算法6中，采用预计算的方式，以存储来换空间，达到提高多标量乘运算的目的。

4.2 Shamir-ZLMOF算法性能分析

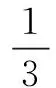
表6 三种算法计算复杂度比较

通过表6中的数据可以发现，Shamir-ZLMOF算法的倍点运算尽管比Shamir算法有时要多1，但是点加运算的次数比起Shamir算法要少很多。Shamir-ZLMOF算法的点加运算次数与Shamir-NAF算法相同，但是倍点运算次数大多数情况下要少。因此Shamir-ZLMOF算法比起以上两种算法具有更高的执行效率。

5 结束语

文中首先分析了当前主流的标量乘和多标量乘算法。在对MOF算法研究的基础上利用左移性质提出了ZLMOF算法，然后利用Homer规则采用连续倍点运算，进一步提高算法的效率。ZLMOF算法的倍点运算效率比起像NAF等传统算法明显要高。紧接着结合滑动窗口法提出了ZLMOF—滑动窗口算法，采用预计算进一步提高运算速率。同时，结合Shamir算法和ZLMOF算法提出了Shamir—ZLMOF算法。新算法比传统的Shamir—NAF算法效率要高。

[1]DiffieW,HellmanM.Newdirectionsincryptography[J].IEEETransactionsonInformationTheory,1976,22(6):644-654.

[2]RivestRL,ShamirA,AdlemanLM.Amethodforobtainingdigitalsignaturesandpublickeycryptosystem[J].CommunicationsoftheACM,1987,21(2):120-126.

[3]KoblitzN.Ellipticcurvecryptosystems[J].MathematicsofComputation,1987,48(177):203-209.

[4]MillerVS.Useofellipticcurvesincryptography[C]//Advanceincryptology.[s.l.]:Springer,1986:417-426.

[5]HuangX,ShahP,SharmaD.FastalgorithminECCforwirelesssensornetwork[C]//Proceedingsoftheinternationalmulticonferenceofengineersandcomputerscientists.[s.l.]:[s.n.],2010:17-19.

[6]BalasubramaniamP,KarthikeyanE.Ellipticcurvescalarmultiplicationalgorithmusingcomplementaryrecoding[J].AppliedMathematicsandComputation,2007,190(1):51-56.

[7]OkeyaK.Signedbinaryrepresentationsrevisited[C]//ProceedingsofCRYPTO'04.[s.l.]:[s.n.],2004:123-139.

[8]KodaliPK,BudwalHS.HighperformancescalarmultiplicationforECC[C]//Internationalconferenceoncomputercommunicationandinformatics.Piscataway:IEEE,2013:1-4.

[9]SolinasJA.Animprovedalgorithmforarithmeticonafamilyofellipticcurves[C]//Advancesincryptology.[s.l.]:[s.n.],1997:357-371.

[10]ShahPG,HuangX,SharmaD.Slidingwindowmethodwithflexiblewindowsizeforscalarmultiplicationonwirelesssensornetworknodes[C]//Internationalconferenceonwirelesscommunicationandsensorcomputing.[s.l.]:IEEE,2010:1-6.

[11]SolinasJA.Low-weightbinaryrepresentationsforpairsofintegers[R].[s.l.]:CentreforAppliedCryptographicResearch,2001.

[12]ZhangJZ,KouYZ,WangT,etal.Faultanalysisonellipticcurvecryptosystemswithslidingwindowmethod[J].JournalonCommunications,2012,33(1):71-78.

[13]YongKL,IngridV.AcompactarchitectureforMontgomeryellipticcurvescalarmultiplicationprocessor[M].[s.l.]:Springer,2007:115-127.

Research on Improved Scalar Multiplication Algorithm Based on MOF

YUAN Yong1,2,3,TANG Gang3,CHEN Hui-yan2,WAN Zong-jie2,ZHANG De-xin3

(1.Xidian University，Xi’an 710071,China;2.Beijing Electronic Science & Technology Institute,Beijing 100070,China;3.China Software Testing Center,Beijing 100044,China)

Scalar multiplication in elliptic curve cryptography scheme takes up the most computing time to consume,so the scalar multiplication operation determines the efficiency of the implementation of cryptographic schemes.In order to improve the execution speed of scalar multiplication,many solutions have been suggested,such as NAF,MOF and so on.After studying a great large number of scalar multiplication algorithm,a ZLMOF algorithm is proposed based on the MOF algorithm.Under the Hamming weight almost remaining unchanged,the minimum length of bit string of the improved algorithm reduces to perfect than that of the original algorithm and then reduces the frequency of the point addition.Then a more efficient ZLMOF-sliding window algorithm is presented combined with sliding window algorithm than NAF-sliding window algorithm and then reduces the frequency of the point addition.Finally,a more efficient Shamir-ZLMOF multi-scalar multiplication algorithm is put forward to refer to the Shamir algorithm than the Shamir-NAF algorithm and then reduces the frequency of the point addition.

scalar multiplication;ZLMOF algorithm;ZLMOF-sliding window algorithm;Shamir-ZLMOF algorithm;elliptic curve

2015-09-01

2015-12-15

时间：2016-11-21

国家发展改革委信息安全专项项目(发改办高技[2010]3044号)

袁 勇(1989-)，男,硕士，研究方向为信息安全、椭圆曲线及其密码方案。

http://www.cnki.net/kcms/detail/61.1450.TP.20161121.1633.006.html

TP301.6

A

1673-629X(2016)12-0111-06

10.3969/j.issn.1673-629X.2016.12.025