遗传算法求解电力设施选址问题
2016-02-23莫汉培陈秋良张子臻
莫汉培,陈秋良,张子臻
(1.东莞供电局,广东 东莞 523000;2.中山大学 移动信息工程学院,广东 珠海 519000)
遗传算法求解电力设施选址问题
莫汉培1,陈秋良2,张子臻2
(1.东莞供电局,广东 东莞 523000;2.中山大学 移动信息工程学院,广东 珠海 519000)
电力系统设施选址优化问题是电力系统规划和设计中的一个基础性问题,可以抽象成约束型的p-中位(p-median)问题,这是一个经典的NP-hard问题。该问题可以描述为从一个点的集合中选择p个有容量限制的中位点,让它们去服务一些有需求的点(客户),要求每一个中位点都不超出容量,并且总花费最小。文中针对这一优化问题,在经典遗传算法的基础上,提出了一种改进的遗传算法,并混合使用局部搜索算法,进行问题的求解。该算法能够利用遗传算法的全局收敛性,并且有效克服遗传算法的局部收敛和早熟问题,从而得到更准确的近似解。最后,使用网上的公开测试数据集以及经地理信息平台(GIS)收集的某供电局的坐标信息进行实验验证。结果表明,提出的算法能够有效解决设施选址问题,并且为企业提供切实可行的方案。
设施选址;遗传算法;约束型p-中位问题;GIS平台
1 概 述
在电力系统的规划和设计中,确定服务设施点比如变电站的位置是非常基础性的工作,这对于后期设备的维护、工作人员的调度都有很大影响。在实际的情形中,由于服务点数量庞大,地理位置信息相对复杂,以及人员容量等限制条件较多等原因导致该问题求解困难。
设施选址问题[1-2]是一个经典的组合优化问题,这个问题可以描述为在一片区域内有一些服务点,这些服务点都有一定的需求服务量,要从中选择p个设施点来服务这些服务点,并且要求满足一定的限制。文中所考虑的是约束型p-中位问题,这个问题是设施选址问题的一种常见形式,在实际生产生活中应用广泛,并且在运筹学、组合调度等领域都有研究。约束型p-中位问题已经被证明是一个NP-hard问题,因此精确解无法在多项式时间内得到,所以人们都倾向于使用现代启发式算法或者一些近似算法以得到问题的近似最优解。
近些年来,许多学者提出的一些解决方法都是基于启发式算法思想的。文献[3-5]提出了一种基于禁忌搜索的方法,主要是通过禁忌表的方法来改善局部搜索陷入局部最优解的问题;文献[6-7]提出用模拟退火的方法解决p-median问题,同样也是用一种退火机制来跳出局部最优解;文献[8]采用双层模拟退火算法,外层对设施选址决策进行优化,内层则在上层确定的设施选址决策基础上,进行用户需求分配的优化;文献[9-10]使用了蚁群算法来求解;文献[11]使用了局部搜索的方法;文献[12-14]使用了遗传算法来求解。随着研究的深入,越来越多的学者倾向于改进传统的启发式算法并且混合使用多种方法来提高算法的性能或者减少时间复杂度。例如,文献[15-16]使用禁忌搜索和遗传算法混合求解这一类问题,并得到了较好的结果。
禁忌搜索、模拟退火、遗传算法等启发式算法可能受到待求解问题不同条件的影响,在时间、效率、精确度等方面表现出一些差异。在问题规模比较大时,以遗传算法为代表的进化类算法以其优良的自适应性和学习性表现出比较好的性能。
文中针对约束型p中位问题,在经典遗传算法的基础上,提出了一种改进的遗传算法,并混合使用局部搜索算法,进行问题的求解。
2 问题建模
文中所讨论的电力系统设施选址问题将优化目标抽象为距离的花费,目标是使得服务点到设施点的距离总和最小(当然,这个目标根据不同的问题情境是可以进行修改的)。将该电力设施选址问题从现实世界中抽象出来,并用数学语言建模成约束型p-中位问题(Capacitatedp-MedianProblem,CPMP),具体描述如下:
假设有一个无向图G={V,E},V为顶点,E为无向边。假设无向图是全连通的,即每两个点之间都有一条边。那么这个问题可以描述为从无向图的顶点集合V中寻找数量为p的子集,并且满足以下约束:
(1)
s.t.

(2)
(3)

(4)
上面的模型中出现的数学符号的含义为:
V={1,2,…,n}是所有服务点集合,同时也是候选的设施点(medians)集合;
dij是服务点i到服务点j的距离;
xij表示分配与否,xij=1表示服务点i分配到设施点j,反之xij=0表示没有分配;
xjj表示是否被选为设施点,xjj=1表示点j被选为设施点,反之xjj=0表示没被选;
qj表示点j的需求量;
Qj表示设施点j的容量。
式(1)是该选址问题的目标函数,即目标为最小化所有服务点(也称客户点,下同)到它所分配的设施点(medians)的距离总和;式(2)要求每一个服务点都分配了惟一一个设施点;式(3)表示一共选取了p个设施点;式(4)表示每一个设施点都不能超过它的容量限制。
3 遗传算法
遗传算法(GeneticAlgorithm)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法,它最初由美国J.Holland教授于1975年首先提出。利用遗传算法求解优化问题的基本思想是:把需要求解的问题模拟成一个生物进化的过程,通过复制、交叉、突变等操作产生下一代的解,并逐步淘汰掉适应度函数值低的解,增加适应度函数值高的解。这样进化N代后就很有可能会进化出适应度函数值很高的个体,算法能够保证求解时的收敛性。
运用遗传算法求解组合优化问题的主要步骤为:染色体编码,适应值计算,种群选择,交叉,变异等。以下将结合电力设施选址问题对遗传算法进行具体说明。
3.1 染色体编码
染色体编码,就是要将待求解问题的解表示成基因串的形式,这样才能使用遗传算法进行求解。
在电力设施选址的问题中,由于可供选址的设施点是空间离散分布的,所以采用p个设施点的索引(编号)来进行染色体的编码。首先给所有可选择的设施点编号(1,2,…,n),在遗传算法中每一条染色体有p个基因,每一个基因就是一个设施点的编号。因此,如果p=5,那么染色体gene可能表示成gene={index1,index2,…,index5},其中index表示可供选择的设施点的编号1,2,…,n。需要特别注意的是,这里的基因是没有顺序的,即染色体{1,3,2}和{1,2,3}是一样的,这对于后面交叉操作时防止同一条染色体出现重复基因有很大作用。
3.2 适应值计算
遗传算法中使用适应值来表示解得优劣,并作为后续选择操作的依据。在大多数情况下,人们通常将目标函数映射成函数值非负的适应值函数。得到一条染色体之后,定义染色体的适应值为所有服务点到该点所分配的设施点的距离总和。首先,忽略地理环境的复杂信息,考虑两点之间的欧氏距离。目标是最小化距离总和D,如何给所有的服务点分配一个设施点分配以达到该目标。这是一个广义分配问题(GeneralAssignmentProblem,GAP),也是一个NP-hard问题。长期以来,有许多方法被用来解决这一问题,例如经典的贪心算法、基于“优先级”的分配算法、拉格朗日松弛等等。
考虑到计算的复杂性和时间性能,文中采用基于优先级的贪心分配策略,它的时间复杂度不高而且效果较理想,能够较好地解决这一问题。该算法的具体流程描述如下:
对于一个服务点c,计算它到所选取的每一个设施点的距离,然后对得到的距离值进行排序。记服务点到最近的设施点的距离为d1,到次近的设施点的距离为d2,那么服务点c的优先级为:
Priority(c)=d2-d1
首先算出所有服务点的优先级,然后按照优先级从高到低进行分配,优先级越高的优先分配设施点给它。对此,可以这样理解,优先级越高的服务点,说明离它最近的设施点和次近的服务点相差越大,如果到后面给它分配,一旦离它最近的设施点的容量已经满了,那么就会增加很大的花费,这是不符合需求的。因此基于这种优先级的贪心方法,可以较好地解决这个分配问题。
3.3 选 择
选择是遗传算法中非常重要的一步,选择的目的是把优化的个体(或解)直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。选择操作是建立在群体中个体的适应度评估基础上的。计算出每条染色体的适应值之后,就可以采取一定的选择策略来对种群进行选择。
常用的选择策略有轮盘赌选择、锦标赛选择等等,这些选择方法都有一定的优缺点。为了防止种群过早陷入局部收敛,同时避免种群的退化,没有采用轮盘赌的选择方法,因为轮盘赌选择很快就会出现大量相同的染色体,从而陷入局部解。
文中采取了一种根据适应值排序的混合选择策略:首先,计算每一条染色体的适应值,并且按照适应值从高到低进行排序;然后,按照适应值进行选择,适应值高的选择保留到后代,在这个过程中需要保证不出现重复的染色体。同时,保留很小比例的最差解,有利于防止局部收敛。
3.4 交 叉
类似于自然界生物进化过程,基因的交叉互换和重组能够产生新的个体,在遗传算法中,通过交叉操作,将大大提高遗传算法的搜索能力,加速求解过程,并期望优秀的基因结合在一起,从而得到更优解。
例如,c={1,2,3,4,5,6}是最优解,而已经得到c1={8,9,3,4,5,6}和c2={1,2,6,7,10,11},那么按照如下的交叉方式进行基因重组:

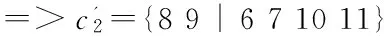
具体来说,根据前面所述的染色体编码方法,将采用如下的交叉算法:
(1)预处理。因为每个设施点只能出现一次,所以要保证在经过交叉之后一条染色体中不会出现两个相同的基因。预处理的方法是:对于参与交叉的两条染色体,计算出染色体相同的部分移到染色体的右边,并将不同的部分移到左边。
(2)当两条染色体不完全相同的时候,进行交叉运算,可以采用经典的单点交叉。



而经过预处理,两条染色体变为:


经过交叉互换得到的新的染色体符合要求。
(3)如果两条染色体完全相同,为了防止陷入局部最优解,采用的方法是引入新的染色体,即随机生成一条新的染色体,并与之另一条进行交换。
3.5 变 异
变异操作是模拟自然界遗传过程中的基因突变,需要注意的是,基于突变是随机发生的,而且概率较低。
遗传算法引入变异操作的主要作用有两个:一是使遗传算法具有局部的随机搜索能力。当遗传算法通过交叉算子已接近最优解邻域时,利用变异操作的这种局部随机搜索能力可以加速向最优解收敛。显然,此种情况下的变异概率应取很小的值,否则接近最优解的状态会因变异而遭到破坏。二是使遗传算法可维持群体多样性,以防止程序出现早熟收敛现象,得不到理想的近似解。
在变异操作中,随机地对染色体的某一个基因进行变异,把这个基因随机替换成另外一个没有出现在染色体中的基因,即服务点的编号。在这个过程中,可以保证一条染色体中不会出现两个相同的基因。比如将c1={2 8 1 4 5 7}进行变异操作,可能得到的结果为:

其中,c1染色体的第5个基因从5变异为3。
3.6 局部搜索
朴素的遗传算法在求解时,需要非常多的迭代次数,才能得到比较好的近似解。为了提高遗传算法的搜索能力,加快收敛速度,减少程序的运行时间复杂度,引入了局部搜索策略。
在完成交叉和变异之后,以一定的比例选取部分染色体进行局部搜索,寻找在这个解得邻域中的更优解。具体的算法流程如下:
首先,对于所选中的染色体的每一个基因c,搜索距离它最近的k个服务点。其中k是一个经验值,k越大,时间复杂度越高,但是k越小,搜索的范围小,优化效果可能也比较小。因为这里是需要做一些局部的优化,所以k尽量选择较小一些,在实验过程中需要调节k值。
然后,把c替换成它邻近的服务点,如果能够得到更优的适应值,则替换它。同样的,这里也需要保证染色体中不出现相同的基因。
经过局部搜索,可以让部分解加速向最优解靠拢,从而加快算法的收敛速度。
4 实验分析
文中利用C++实现了前面描述的算法并进行了实验分析。实验机器的配置为:CPUInteli5 主频2.3GHz,内存8G。
为了验证算法的正确性和有效性,文中采用了两个数据集进行测试和验证。第一个数据集是来自网络上著名的优化问题公开测试数据集—OR-Library(http://people.brunel.ac.uk/~mastjjb/jeb/info.html)。选取了OR-Library中的p-median-capacitated问题的测试数据,测试程序选取其中的10个测试用例,其中5组服务点数量n为50,设施点数目p为5,另外5组服务点数量n为100,设施点数目p为10。
测试结果如表1所示。

表1 第一个数据集上的测试结果
分析测试结果发现,使用文中改进的遗传算法可以有效解决约束型p中位问题。随着服务点和设施点数量的增加,运行的时间也在增加。在运行时间不超过30s的情况下,算法最好的结果误差为2.6%,最坏的结果误差为5.5%。
为了更直观地显示程序运行的结果,将其中一组数据的服务点和经过文中算法求解出的设施点画在图上,如图1所示。
第二个数据集来源于GIS平台收集的数据。该平台是基于高德地图针对某供电局的装置设备坐标定位而开发的。通过该平台,获得了这些客户点的地理信息数据。针对这些数据,对电力设施进行选址,对不同

图1 表1中一组数据,设施点选择和分配结果
的设施点数量p进行实验,结果如表2所示。

表2 利用某供电局装置数据测算结果
5 结束语
文中给出了利用改进的遗传算法解决电力系统设施选址问题的一种实现方法,并且与网上公开测试数据集进行对比,验证了算法的可行性;同时该算法也表现出了良好的时间性能。此外,通过GIS系统收集了某供电局的电力设施数据并使用该方法进行求解,能得出较满意的结果。
当然,在实验过程中发现,提出的算法处理约束型p中位问题时,对于不同的问题规模和数据表现出了一定的效果差异,这说明对于算法在不同情况的性能的稳定性方面还需更深入的工作,加以改进和优化。
[1] 王 非,徐 渝,李毅学.离散设施选址问题研究综述[J].运筹与管理,2006,15(5):64-69.
[2] 杨丰梅,华国伟,邓 猛,等.选址问题研究的若干进展[J].运筹与管理,2005,14(6):1-7.
[3]RollandE,SchillingDA,CurrentJR.Anefficienttabusearchprocedureforthep-medianproblem[J].EuropeanJournalofOperationalResearch,1997,96(2):329-342.
[4]GloverF.Tabusearch-partI[J].ORSAJournalonComputing,1989,1(3):190-206.
[5] 郭崇慧,覃华勤.一种改进的禁忌搜索算法及其在选址问题中的应用[J].运筹与管理,2008,17(1):18-23.
[6]MurrayAT,ChurchRL.Applyingsimulatedannealingtolocation-planningmodels[J].JournalofHeuristics,1996,2(1):31-53.
[7]ChiyoshiF,GalvãoRD.Astatisticalanalysisofsimulatedannealingappliedtothep-medianproblem[J].AnnalsofOperationsResearch,2000,96(1-4):61-74.
[8] 秦 进,史 峰.物流设施选址问题的双层模拟退火算法[J].系统工程,2007,25(2):36-40.
[9] 许 婷,盛 明,娄彩荣.基于GIS和蚁群算法的物流配送中心选址研究[J].测绘科学,2010,35(6):206-208.
[10] 李有梅,陈 晔.一种新的求解约束P-中位问题的启发式算法[J].计算机工程,2005,31(19):162-164.
[11]LorenaLAN,SenneELF.Localsearchheuristicsforcapacitatedp-medianproblems[J].NetworksandSpatialEconomics,2003,3(4):407-419.
[12]Estivill-CastroV,Torres-VelázquezR.Hybridgeneticalgorithmforsolvingthep-medianproblem[M]//Simulatedevolutionandlearning.Berlin:Springer,1999:18-25.
[13]AlpO,ErkutE,DreznerZ.Anefficientgeneticalgorithmforthep-medianproblem[J].AnnalsofOperationsResearch,2003,122(1-4):21-42.
[14]GhoseiriK,GhannadpourSF.Solvingcapacitatedp-medianproblemusinggeneticalgorithm[C]//ProcofIEEEinternationalconferenceonindustrialengineeringandengineeringmanagement.[s.l.]:IEEE,2007:885-889.
[15]GloverF,KellyJP,LagunaM.Geneticalgorithmsandtabusearch:hybridsforoptimization[J].Computers&OperationsResearch,1995,22(93):111-134.
[16] 李大卫,王 莉,王梦光.遗传算法与禁忌搜索算法的混合策略[J].系统工程学报,1998,13(3):28-34.
Solving Grid System Facility Location Problem Based on Improved Genetic Algorithm
MO Han-pei1,CHEN Qiu-liang2,ZHANG Zi-zhen2
(1.Power Grid Co.,Guangdong Dongguan Power Supply Bureau,Dongguan 523000,China;2.School of Mobile Information Engineering,Sun Yat-Sen University,Zhuhai 519000,China)
Grid system facility location,as a basic problem in grid system plan and design,can be modeled as a capacitatedp-medianproblem,whichisaclassicalNP-hardproblem.Itcanbedescribedasselectingp-capacitatedmediansfromaverticessetinordertoserveasetofdemandvertices(customers),sothatthetotalassigneddemandtoeachofthecandidatemediandoesnotexceeditscapacity,andthecostisminimum.Tosolvethisproblem,animprovedgeneticalgorithmincorporatedwithalocalsearchprocedureisproposedbasedonclassicalgeneticalgorithm.Itcanusetheglobalconvergenceandavoidthelocalconvergenceandprematureingeneticalgorithmtoobtainthemoreaccurateapproximatedsolution.Thealgorithmhasbeentestedusingstandardtestingdataandtherealdatacollectedbyageographicinformationsystem.Theresultsshowthatthismethodcanprovideafeasibleandpromisingsolutionfortheindustry.
facility location;genetic algorithm;capacitatedp-medianproblem;NP-hard;GISplatform
2015-01-06
2015-04-10
时间:2016-02-18
中央高校基本科研业务费专项资金(15lgpy37)
莫汉培(1967-),男,助理工程师,主要从事电力系统管理工作。
http://www.cnki.net/kcms/detail/61.1450.TP.20160218.1619.014.html
TP
A
1673-629X(2016)03-0197-05
10.3969/j.issn.1673-629X.2016.03.046
