动态步长的RRT路径规划算法
2016-02-23王道威朱明富
王道威,朱明富,刘 慧
(华中科技大学 自动化学院,湖北 武汉 430074)
动态步长的RRT路径规划算法
王道威,朱明富,刘 慧
(华中科技大学 自动化学院,湖北 武汉 430074)
传统的快速扩展随机树(RRT)算法虽然有很多优良特性,但是由于扩展点的随机选取,规划出来的路径具有很大的随机性。文中在对RRT算法改进的基础上,提出了一种动态步长的RRT路径规划算法。其中步长为RRT生长的最小单位长度。动态步长的RRT算法是在对传统RRT算法的基础上,添加了动态步长的特性,改善了快速扩展随机树的不确定性,提高了避障能力,使得算法确定性和高避障能力兼备。仿真实验结果表明,该算法在路径规划中具有路径确定、速度快和高避障能力的特点。
快速扩展随机树;动态步长;路径确定性;高避障能力
0 引 言
随着无人机、无人汽车等无人智能设备的不断应用和发展,RRT路径规划算法[1-3]越来越多地被应用。RRT算法是一种随机搜索算法,它能在保证系统实时性的前提下,寻找到问题的较优解。但是RRT算法具有随机性[4],规划出来的路径偏离目标点,与理想路径相比有较大差异。
文中在经典RRT算法的基础上引入目标引力函数,让随机树朝着目标点方向生长,使得规划出来的路径更加接近理想路径。但是这种添加了目标引力函数的RRT算法虽然降低了路径的随机性,但同时也降低了算法的避障能力,起始点和目标点障碍物比较多的情况下不能规划出路径。文中在RRT算法的基础上引入了动态步长的概念。步长即为RRT生长的最小单位长度。在RRT算法扩展新节点时,当遇到障碍物时自动减小目标点方向的步长,没遇到障碍物时再恢复原步长。改进后的RRT路径规划算法兼具路径确定性和高避障能力的优点。
1 RRT算法
快速随机扩展树(RRT)算法由Steven M. LaValle于1998年在文献[5]中首先提出。RRT算法是从空间中一个起始节点出发,通过随机采样,不断增加新节点,生成一个随机扩展树。当增加的新节点中有目标节点时,起始节点到目标节点就会至少有一条通路,称为路径。RRT算法已应用于飞行器运动规划[6]和移动机器人路径规划中[7]。
1.1 经典RRT算法
RRT算法的作用是在度量空间X中,选择一条从初始状态点xinit到目标状态点xgoal或者到目标状态点区域xgoal∈X的路径。通常选择距离空间C作为度量空间,即X=C。在度量空间中路径无法通过的区域称为障碍区域,记为xobs∈X。障碍区域在度量空间中的补集称为自由区域,记为xfree∈X。令xrand为每次扩展RRT时在自由区域中随机选取的点,xrand∈xfree。令xnear为每次扩展RRT时在当前RRT中与xrand距离最近的点。xnew为每次新增加的扩展点。给定一个初始状态xinit,一个随机扩展树T,生成K个顶点的方法如下:
GENERATE_RRT(xinit,K,△t)
T.init(xinit);
Fork=1toKdo
xrand←RANDOM_STATE();
xnear←NEAREST_STATE(xrand,T);
u←SELECT_INPUT(xrand,xnear);
xnew←NEW_STATE(xnear,u,△t);
T.add_vertex(xnew);
T.add_edge(xnear,xnew,u);
ReturnT
其中,RANDOM_STATE()在自由空间中随机选取一点xrand,NEAREST_STATE()在当前RRT中选择与xrand距离最近的点xnear,SELECT_INPUT()结合xrand和xnear得到输入u,NEW_STATE()得到新节xnew。
1.2 引入目标引力思想的RRT算法
在文献[1]中介绍了一种引入目标引力思想的RRT算法,能有效减少RRT算法的随机性,让路径朝着目标方向扩展。
在文献[2]中介绍了一种目标偏好RRT算法,该算法大部分扩展过程使用随机点,以一定小概率选取目标点取代随机点,将随机树向目标区域扩展。
文献[3]中对目标偏好RRT算法做了进一步改进,使它应用于非完整微分约束中。
经典的RRT算法随机性比较明显,规划出来的路径非常曲折,不适合实际使用中的路径规划。经典RRT算法新节点位置的计算公式如式(1)所示。
(1)
其中,ρ为RRT生长的最小单位长度,称为步长。
加入目标引力思想的RRT算法新节点位置的计算公式如式(2)所示。
(2)
其中:ρ1为随机点方向的步长;ρ2为目标点方向的步长。
2 动态步长的RRT算法
路径规划是按照某一性能指标搜索一条从起始状态到目标状态的最优或近似最优的无碰路径[8]。动态步长的RRT算法能够规划出比较理想的无碰路径。
2.1 步长对RRT算法的影响
首先考虑步长在经典RRT路径规划算法中的作用。经典随机扩展树生成算法扩展一个新节点的过程为:首先在度量空间中随机选取一点xrand,然后在当前扩展树中(可能为空)找到与xrand距离最近的点xnear,在xnear到xrand的方向上扩展一个步长的距离得到新节点xnew加入扩展树中。
加入目标引力思想后的RRT算法能有效解决路径随机性强的问题。引入目标引力思想后的RRT算法与经典RRT算法相比添加了xgoal方向的分量。加入目标引力思想后,步长的选择对新节点的位置会有影响。此时新节点不再在xnear到xrand的连线上了。当ρ2>ρ1时,新节点偏向于xgoal,由于xgoal的位置通常是固定的,扩展树朝着xgoal方向扩展。当ρ2<ρ1时,新节点偏向于xrand,由于xrand的位置是随机选取的,此时扩展树的扩展方向接近RRT经典算法。
引入目标引力思想后的随机扩展树朝着目标点方向发展,规划出来的路径更加接近理想路径。ρ2相对于ρ1取的越大,扩展树越朝着xgoal方向扩展,规划出来的路径越接近理想路径。
以上所讨论的都在无障碍空间中规划路径,在实际的路径规划应用中,起始点和目标点之间都或多或少存在很多障碍,很难找到一个有效的路径规划方法来应对各种复杂环境[9]。规划出的路径需要避开所有障碍到达目标点。经典RRT算法新节点的添加都是随机方向的,能够有效地避开障碍。引入目标引力的RRT算法常常为了能够使规划出的路径接近理想路径,目标点方向的步长要较大于随机点方向的步长。此时如果起始点和目标点障碍物较多,那么扩展树无法绕开障碍物到达目标点。
可以得出结论:路径理想和避障能力是相互矛盾的。为了解决这对矛盾,在目标引力RRT算法基础上添加了动态步长的概念。当没有遇到障碍物时取ρ2>ρ1,使扩展树尽可能朝着目标点方向扩展。当遇到障碍物时取ρ2<ρ1,使扩展树朝着随机点方向扩展,因为随机点的随机性,新节点也具有随机性,从而可以高效地避开障碍物。
2.2 动态步长RRT算法的优点
经典RRT算法的随机性很强,规划出来的路径与理想路径相差很大,但由于扩展节点的随机性,经典RRT算法具有很强的避障能力。
为了规划出更加理想的路径,在经典RRT算法中引入目标引力思想,让新节点朝着目标节点的方向扩展。但是这种算法的避障能力很弱,当起始点和目标点间有很多障碍的时候不能规划出路径。
动态步长RRT算法具有以上两种算法的优点,不仅能朝着目标节点扩展新节点,而且具有和经典RRT算法一样的避障能力。动态步长RRT算法在路径规划中更加实用。和经典RRT算法一样,该算法具有高效的搜索特性,使其适合解决高维空间多自由度的复杂约束下的运动规划问题,能直接应用到非完整性约束或非完整性动力学约束规划中[10]。
动态步长RRT算法时间复杂度低。在文献[11-13]中介绍的滚动规划算法,每次在一个窗口中规划出最优路径,时间复杂度很高。动态步长RRT算法在扩展每一个新节点时,只需计算一个式(2)的值。很多类似文献[4]中提出的RRT改进算法,在扩展一个新节点时计算若干个随机点的估价函数,选取估价函数值最小的作为新节点。这些做法使算法时间复杂度成倍增加。因为RRT扩展树一般都具有非常多的节点,所以保持算法的较低的时间复杂度非常重要。
3 仿真实验结果分析
实验环境:Windows Embedded 8.1, Intel® CoreTMi5-3317U CPU @ 1.70 GHz, 内存8 G。
编译工具:Visual Studio 2013。
图1~5中左下角为起始节点,右上角为目标节点。图中空心圆环为障碍物,距障碍物环心40个单位长度内的区域为障碍区域。图中黑色粗线和黑色细线共同构成随机扩展树,黑色粗线连接起始点和目标点,被选为规划出的路径。
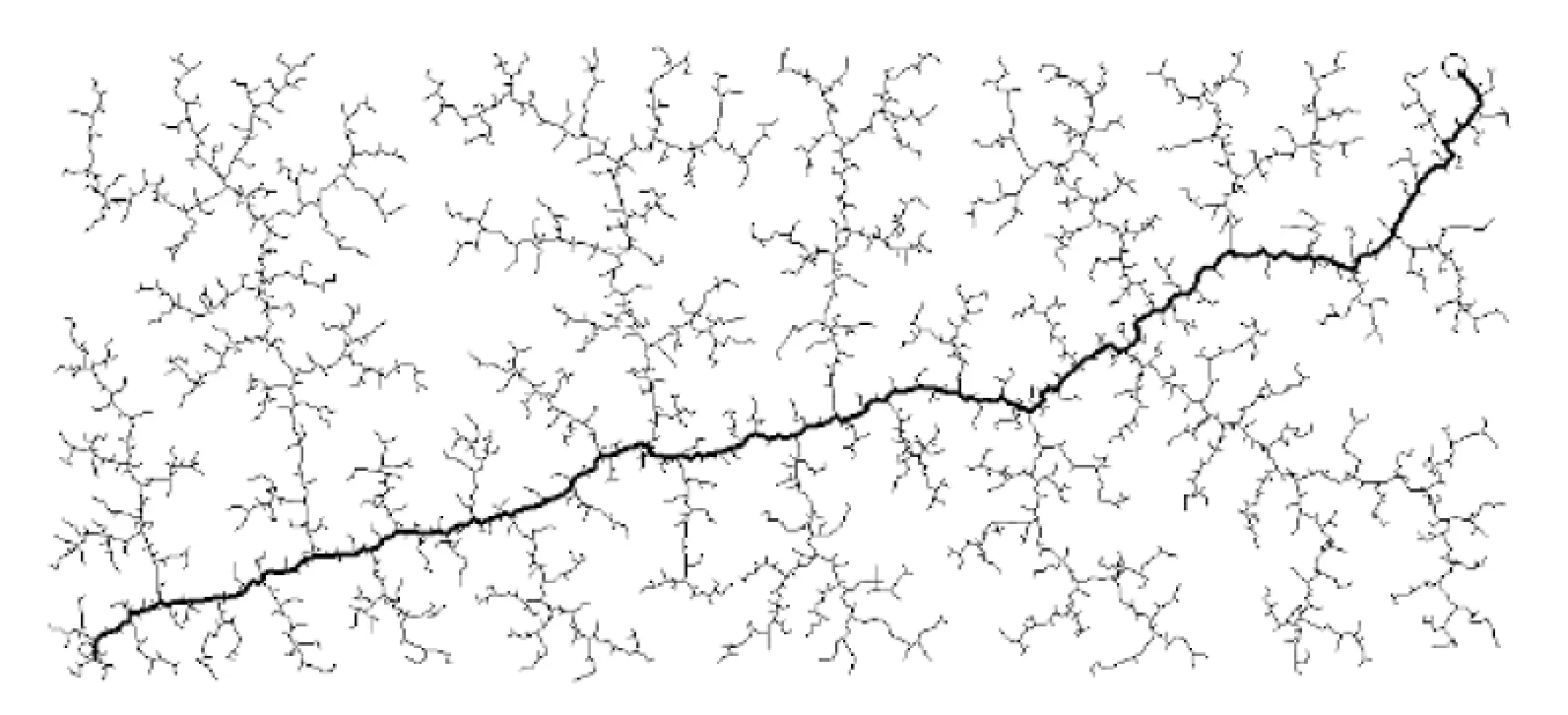
图1 经典RRT算法(无障碍)
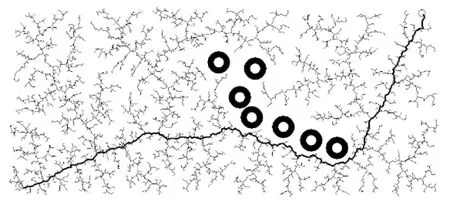
图2 经典RRT算法(有障碍)
在无障碍的情况下,如图1、3、4所示,都能规划出路径。由图1可见,经典RRT算法的随机性较强,路径比较曲折。由图3、4可见,目标引力RRT算法和动态步长RRT算法在无障碍情况下效果相同,规划出的路径比较接近理想路径。

图3 目标引力RRT算法(无障碍)

图4 动态步长RRT(无障碍)
图5 动态步长RRT(有障碍)
在有障碍的情况下,如图2、5所示,目标引力RRT算法无法规划出路径,其他两种算法都能规划出路径。由图2可见,经典RRT算法能有效避开障碍物,但是随机性较强。目标引力RRT算法在有障碍的情况下,由于起始点和目标点障碍物过多,随机树无法绕开障碍物到达目标节点,导致运行程序无响应。由图5可见,动态步长RRT算法能有效避开障碍物,而且没有经典RRT算法的随机性。
4 结束语
经典RRT算法具有随机搜索特性[14],因此具有很强的避障能力,而且生成的路径不够光滑,与理想路径相差很远。目标引力思想RRT算法牺牲了部分随机性,规划出的路径更加光滑,但是减弱了避障能力,很多情况下无法规划出路径。动态步长的RRT算法不仅能够规划出接近理想路径的路径,而且具有很强的避障能力,算法时间复杂度低,能够高效广泛地应用在实际路径规划中。
[1] 郝利波,侯媛彬.基于一种改进RRT算法的足球机器人路径规划[J].西安科技大学学报,2011,31(1):81-85.
[2] Urmson C,Simmons R.Approaches for heuristically biasingRRTgrowth[C]//ProcofIROS.[s.l.]:[s.n.],2003:1178-1183.
[3] 徐 娜,陈 雄,孔庆生,等.非完整约束下的机器人运动规划算法[J].机器人,2011,33(6):666-672.
[4] 王 滨,金明河,谢宗武,等.基于启发式的快速扩展随机树路径规划算法[J].机械制造,2007,45(12):1-4.
[5]LaValleSM.Rapidly-exploringrandomtrees:anewtoolforpathplanning[R].Ames:IowaStateUniversity,1998.
[6]AminJN,BoskovicJD,MehraRK.Afastandefficientapproachtopathplanningforunmannedvehicles[C]//ProcofAIAAguidance,navigation,andcontrolconference.Keystone,Colorado:AIAA,2006:1-9.
[7] 樊晓平,李双艳.带滚动约束轮移式机器人动态规划的研究[J].控制与决策,2005,20(7):786-788.
[8] 李 磊,叶 涛,谭 民,等.移动机器人技术研究现状与未来[J].机器人,2002,24(5):475-480.
[9] 宋金泽,戴 斌,单恩忠,等.一种改进的RRT路径规划算法[J].电子学报,2010,38(2A):225-228.
[10]JouandeauN.Rapidly-exploringsortedrandomtree:aselfadaptiverandommotionplanningalgorithm[J].LectureNotesinElectricalEngineering,2009,24(5):63-73.
[11] 席裕庚.动态不确定环境下广义控制问题的预测控制[J].控制理论与应用,2007,17(5):665-670.
[12] 赵春霞,唐振民,陆建峰,等.面向自主车辆的局部路径规划仿真系统[J].南京理工大学学报:自然科学版,2002,26(6):570-574.
[13] 张纯刚,席裕庚.全局环境未知时基于滚动窗口的机器人路径规划[J].中国科学:E辑,2001,31(1):51-58.
[14] 康 亮,赵春霞,郭剑辉.未知环境下改进的基于RRT算法的移动机器人路径规划[J].模式识别与人工智能,2009,22(3):337-343.
Rapidly-exploring Random Tree Algorithm Based on Dynamic Step
WANG Dao-wei,ZHU Ming-fu,LIU Hui
(School of Automation,Huazhong University of Science and Technology,Wuhan 430074,China)
Although the traditional Rapidly-exploring Random Tree (RRT) algorithm has many good features,there is a lot of randomness in path planning of RRT because of the random selection of the vertex.Based on the improvement of RRT algorithm,a new RRT path planning algorithm of dynamic step size is proposed in this paper.The step size is the minimum unit length when RRT exploring.Based on traditional RRT,the dynamic step size is added,avoiding the uncertainty,and the obstacle avoidance capability is improved,thus the path planning of RRT algorithm has both obstacle avoidance ability and high certainty.The results of simulation experiments show that the algorithm has the features of avoiding the uncertainty,fast speed and obstacle avoidance in path planning.
RRT;dynamic step size;path planning certainty;obstacle avoidance
2015-06-30
2015-09-30
时间:2016-02-18
国家自然科学基金资助项目(61403154)
王道威(1989-),男,硕士研究生,研究方向为多智能体控制、图像处理。
http://www.cnki.net/kcms/detail/61.1450.TP.20160218.1638.086.html
TP301.6
A
1673-629X(2016)03-0105-03
10.3969/j.issn.1673-629X.2016.03.025
