基于Hadoop平台的SVM_KNN分类算法的研究

李正杰，黄 刚

(南京邮电大学 计算机学院，江苏 南京 210003)

基于Hadoop平台的SVM_KNN分类算法的研究

李正杰，黄 刚

(南京邮电大学 计算机学院，江苏 南京 210003)

数据的变革带来了前所未有的发展，对丰富且复杂的结构化、半结构化或者是非结构化数据的监测、分析、采集、存储以及应用，已经成为了数据信息时代发展的主流，分类和处理海量数据包含的信息，需要有更好的解决方法。传统的数据挖掘分类方式显然已经不能满足需求，面对这些问题，这里对数据挖掘的一些分类算法进行分析和改进，对算法进行结合，提出了改进的SVM_KNN分类算法。在这个基础上，利用Hadoop云计算平台，将研究后的分类算法在MapReduce模型中进行并行化应用，使改进后的算法能够适用于大数据的处理。最后用数据集对算法进行实验验证，通过对比传统的SVM分类算法，结果表明改进后的算法达到了高效、快速、准确、低成本的要求，可以有效地进行大数据分类工作。

数据挖掘；Hadoop；并行化；SVM_KNN

0 引 言

当下的时代是一个急需对数据进行高效快速挖掘的时代，而分类是数据挖掘的一项首要任务和技术。分类可以看成是数据库到一组类别的映射，需要构造一个分类器，输入一个样本数据集，通过在训练集中的数据表现出来的特性，为每一个类找到一种准确的描述或者模型[1]，从而利用分类对未来的数据进行预测。SVM算法非常适合解决结构复杂的数据，而针对SVM算法的缺点，KNN算法可以简单有效地弥补。文中结合这两种算法，并对其加以改进，来对数据进行更精确的分类。庞大而复杂的数据对数据分类处理的准度和精度有着极高的需求，互联网和计算机技术的发展产生了云计算技术，Hadoop则是其中的优秀代表。Hadoop是可由大量低成本计算机构成的，能够可靠地分布式处理大数据的软件框架，是一个可以进行云计算应用和研究的平台。云计算技术的出现为数据挖掘的发展提供了强大的推动力，将Hadoop应用于数据挖掘技术中，对数据挖掘分类算法进行并行化处理后，在Hadoop云平台上运行，可以极大提高数据挖掘分类的准确性和效率。

1 Hadoop平台

Hadoop以HDFS[2]和MapReduce[3]为核心。HDFS参照了谷歌的分布式文件系统(GFS)，是Hadoop的分布式文件系统，为分布式的计算提供了底层的支持。它的机制和以前的分布式文件系统有很多相似之处，但是HDFS以大数据、大文件和低成本等要求进行了设计，而且容错率比较高，适合布置在低成本的计算机上，能够提供非常大的系统吞吐量并处理一些非常大的文件。而MapReduce是Hadoop的技术核心，它是为大数据处理提供的可以利用底层分布式环境的编程模型，在不用关心底层细节的情况下为用户提供接口，这让它显得非常简单，而且具有强大的可扩展性和可伸缩性。MapReduce编程模型的计算过程分为两部分：Map阶段和Reduce阶段，即映射与规约。Map阶段就是将一个任务分解成多个任务，Map把原始的数据通过函数定义的映射过程进行转换和过滤，获得中间的数据作为Reduce阶段的输入，然后对生成的中间数据也按照函数定义的处理过程进行规约处理，Reduce会获得最终的结果。Hadoop可以充分利用集群中的节点进行大规模数据存储和高速运算[4]。

Hadoop具有可靠、可扩展、高效、高可用性、低成本和具有完备的容错机制等优点。基于这些优点，Hadoop被诸如IBM、亚马逊、雅虎、百度、腾讯和阿里巴巴等企业大量运用和改善，用以开发更完善的云计算平台[5-6]。

2 数据挖掘分类方法的基本原理

对数据进行合理有效的分类在数据挖掘的整个过程中显得十分重要。分类的目的是构造出一个分类器，分类器再把数据库中的数据项和给定类别中的某一个类别对应起来,实现分类的目的，然后进行预测分析。分类是否有效准确将会直接影响到数据挖掘最终结果的有效性和准确性[7]。分类在医疗、模式识别、信息等领域应用广泛。

数据挖掘分类一般分成两个步骤：建立模型和使用模型。要对数据进行有效的挖掘，首先需要通过分析数据库中元组来构造一个模型，用来对预定的数据类集进行描述。这些数据库元组被称为训练数据集，训练集中的单个元组被称为样本，每个样本有一个特定的类标签和它对应。一般情况下，学习的模型可以由分类规则、决策树或者等式、不等式等形式提供，这些规则可以为后面的数据样本进行分类，即第二步使用模型进行分类。在使用之前，首先需要评估模型的预测准确率，评估过后如果认为可以接受模型的准确率，那么就可以开始使用模型对未知的数据进行分类。

目前来说，分类模型的构造主要有以下方法：统计、机器学习和神经网络等。统计方法主要包括贝叶斯法、一些常见的近邻算法和基于事例的学习[8]等。机器学习方法包括规则归纳法，如决策表、产生式规则和决策树法(如决策树、判别树)。而神经网络方法主要则是BP算法，一种非线性的判别函数[9]。一些如粗糙集等方法也可以用来构造分类器。大体上，分类的方法主要有基于距离的分类方法、贝叶斯分类方法、决策树分类方法、规则归纳方法等。具体则有许多不同的算法，像支持向量机算法、K-近邻算法、朴素贝叶斯算法、C4.5算法、AQ算法等。

3 SVM_KNN分类算法

3.1 SVM算法

支持向量机(Support Vector Machine,SVM)算法是在1995年由Vapnik提出的[10]，一种基于统计学习理论和结构风险最小化理论的机器学习方法[11]。它是针对两种类别分类的算法，具有优秀的泛化能力，适合于解决那些维度高的非线性数据的问题，因此在分类、识别、检索等方面得到了非常广泛的应用。

SVM算法的基本思想在于：找到一个最优分类超平面，它能满足分类的要求和精度，并且超平面的两侧空白空间能够最大。如图1和图2所示，两幅图中的

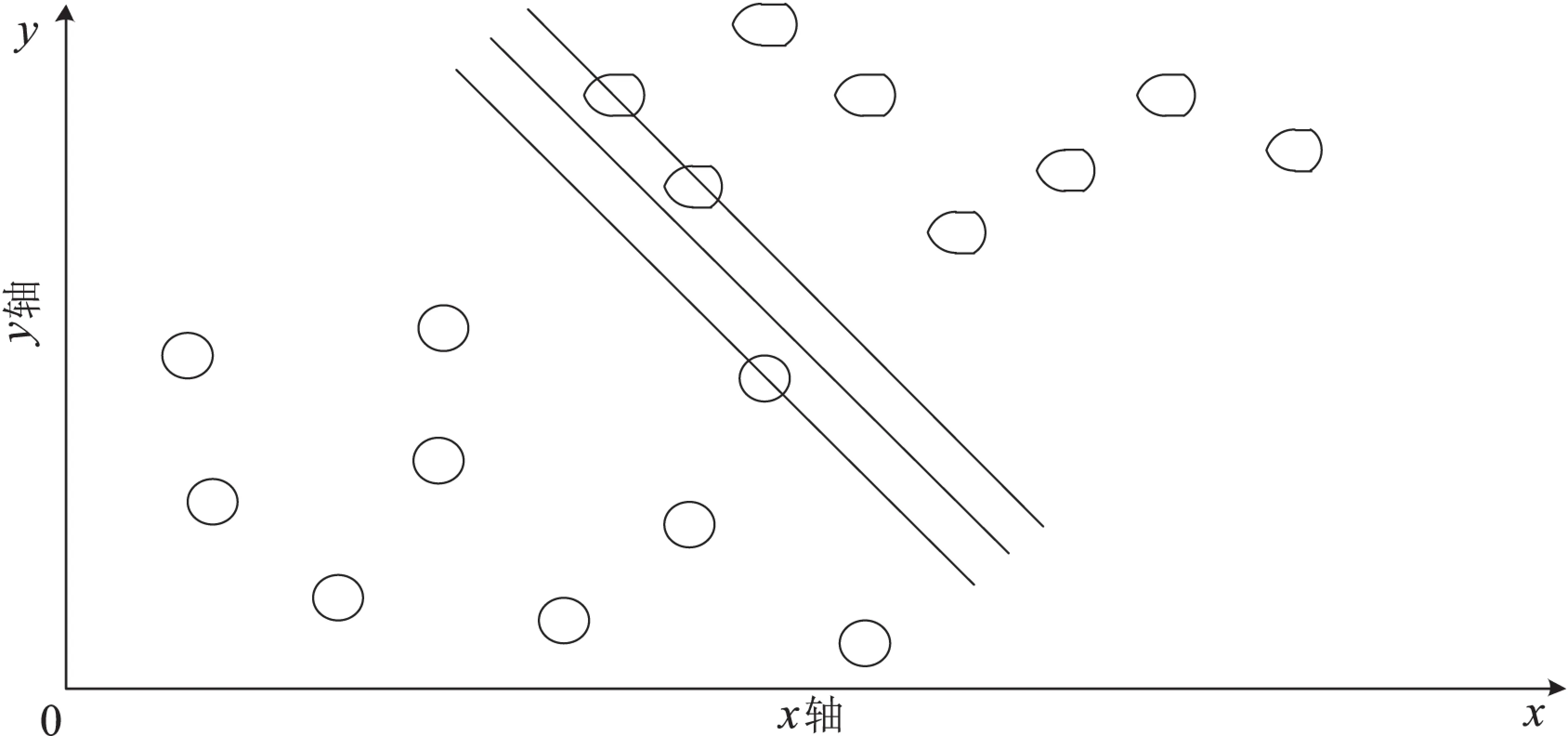
图1 一般分类超平面

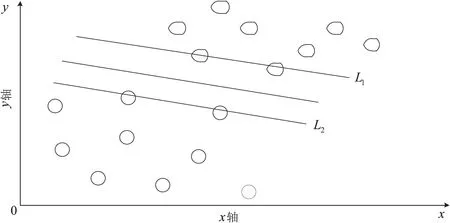
图2 最优分类超平面

超平面均能起到分类的效果，但是图2中超平面两侧空白的空间最大，所以它是最优分类超平面，而分隔边界如L1,L2上的样本点称为支持向量。

(1)

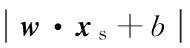
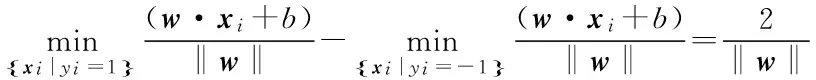
(2)

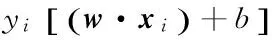
(3)

构造拉格朗日函数即可求得最终的决策函数为：

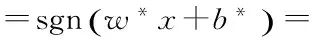
(4)

其中:ai是拉格朗日系数;b*是分类阈值。

如果训练样本线性不可分，那么则需要引入非负松弛变量εi,i=1,2,…,n，则其最小化函数为：

(5)

其中,C是一个惩罚参数。

对于非线性的样本集，需要通过一种非线性的映射将输入向量映射到一个高维特征空间，在这个空间里构造出最优分类超平面。这种非线性的变化可以通过核函数来转变[12]。

3.2 KNN算法

KNN(K-NearestNeighbor)算法是由Cover和Hart于1968年提出的[13]，一种基于距离、基于实例的非参数方法。KNN算法是一种懒惰的学习算法，它的基本思想比较容易理解：空间中的每一个训练数据都作为一个点，给出一个需要测试的数据，在这个空间中通过相似度算法找出与这个待测试数据最相似的K个最近邻点，统计出这K个最近邻点中哪个类的个数最多，则认为测试数据属于该类,如图3所示。

当K=4时，4个最近邻点中有3个I类点，一个II类点，所以认为待测数据属于I类；当K=7时，7个最近邻点中有3个I类点，4个II类点，所以此时认为待测数据属于II类。

3.3 SVM_KNN分类算法原理及其改进

KNN算法虽然简单有效，但是仍然存在很多不足。在KNN算法中，对于每一个待测数据都需要计算它与空间中每个样本的相似度后，才能进行比较，得到K个最近邻点，因此KNN算法的计算量比较大。另外，由于算法对每个样本都赋予了相同的权重，认为每个特征对分类的作用都是一样的[14]，所以当样本的分布不是很平均时，可能会导致输入的待测数据被分到样本容量大的那一方，造成错误分类的情况。

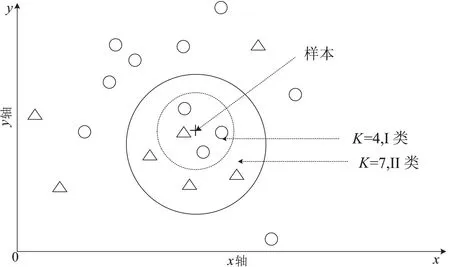
图3 KNN算法示例

而对于SVM算法，Vapnik通过分析指出，在对两个类别进行分类时，SVM算法在两个类别的边界区域或重叠区域的样本会存在一定的分类错误[10]，经过对误分样本的分布情况进行研究后，可以发现SVM算法一般误分都发生在最优分类面的附近[15]。

SVM分类器可以看作是每个类只有一个代表点的最近邻分类器[15]，所以可以考虑将SVM算法和KNN算法结合起来产生一种新的算法，即SVM_KNN算法，在这个基础上，对SVM算法选取合适的惩罚参数和核函数，文中采用的核函数为径向基核函数。对KNN算法采取加入权重系数的方式，权重系数可以通过某个类的样本数占所有样本数的比重来求得，在计算待测数据到某个类样本的距离时，用这个类的权重系数乘以距离，所得的结果作为比较依据，使得样本容量大的一类占的权重变小，样本容量小的一类占的权重变大，来尽可能避免样本分布不均所带来的分类影响。同时，还可以使用效果更稳定的向量空间余弦相似度来代替KNN算法中的欧氏距离相似度。改进后的SVM_KNN算法对原来的两种算法进行了优劣互补，在性能上进行了优化，也不需要KNN算法进行大量的计算，提高了分类的准确性。

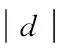
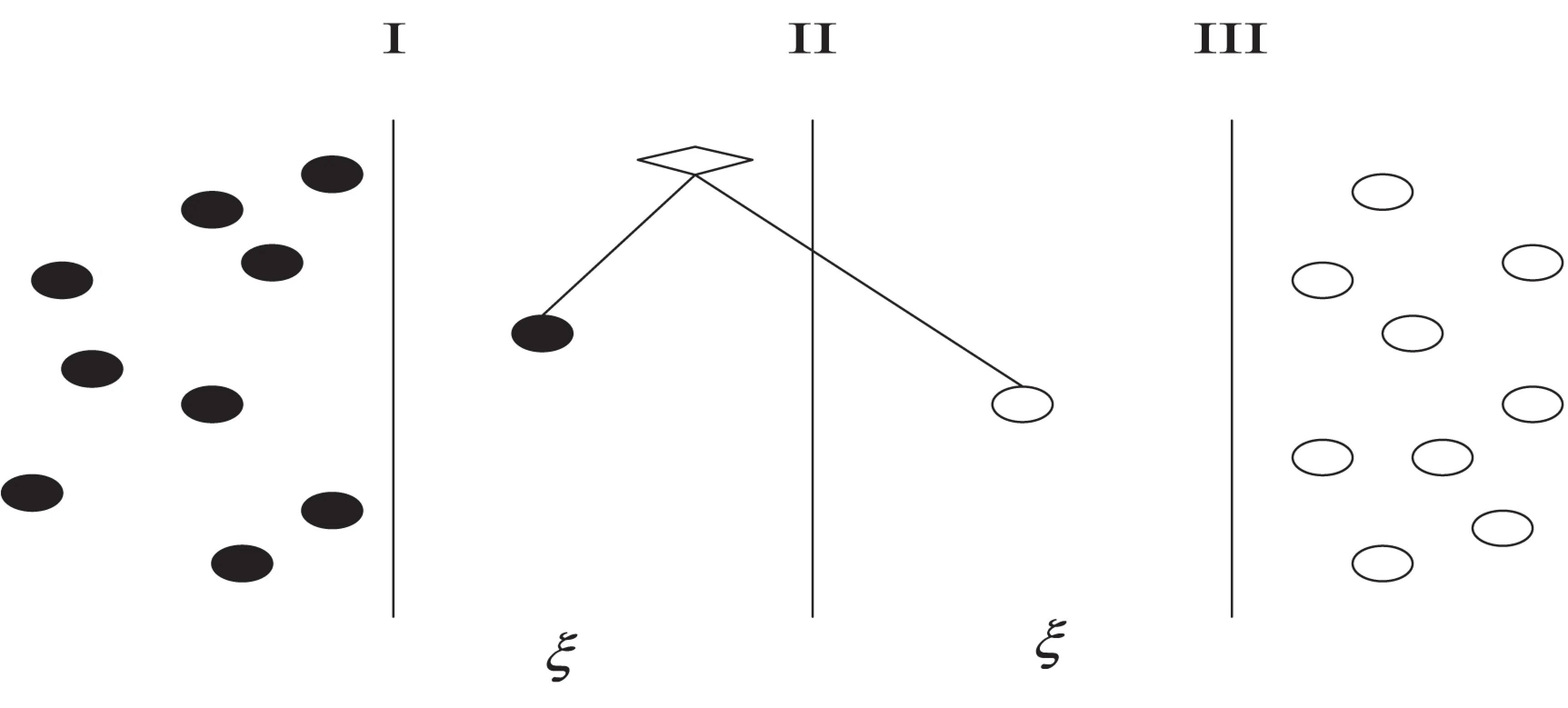
图4 SVM_KNN算法

SVM_KNN算法的主要实现步骤如下：

(1)采用样本训练集对SVM算法进行训练，求出分类决策函数(式(4))中的系数w和常数b，得到支持向量集Dsv，给定阈值ξ，并对测试数据集D进行预处理；

(2)若D为空，则停止步骤的进行，若D不为空，则从D中取出待分类数据x；

(4)若dis>ξ，则选定好合适的核函数，用SVM算法进行分类，最后输出式(4)的f(x)；

(5)若dis<ξ，则使用KNN算法进行分类，选定好K的值，输入待分类数据x，用支持向量集Dsv作为样本点，在距离计算中加入权重系数平衡样本，输出最后的结果；

(6)从测试数据集D去除已分类好的数据x，返回步骤(2)继续执行。

3.4 SVM_KNN分类算法的并行化处理

从上文可知，首先需要用样本训练集对SVM算法进行训练，而SVM算法主要是找出支持向量，稀疏性是支持向量的特性，即支持向量在训练样本集中占的比例很小。利用这个特性，可以先对数据量大的训练数据集进行分块处理，因为各个分块一般来说具有独立性，可以将其并行化处理，分块处理进行训练可以减少SVM算法的训练时间。

对于分好的小数据集，可以采用SMO算法[16]进行训练以加快效率得到每个小数据集的支持向量集，当然不能简单地通过叠加每个小数据集的支持向量集得出最后整个训练数据集的支持向量集，这样可能导致得到的支持向量集有着明显的偏差。因此在对大数据集进行分块时，应保持分块的均衡性，使得每个分块不同类别的比例和原有比例相近，对每个分块进行训练，过滤非支持向量点，保留支持向量点，然后两个分块的训练结果经过整合后作为下一个输入。就这样一直迭代直到剩下最后一个支持向量集，然后判断这个集合是不是达到了迭代精度，如果达到了，则输出最后得到的支持向量集、系数w和常数b。通过对初始数据集进行分块处理，可以极大提高SVM算法的训练速度，也使训练准确度有一定的保证。

训练好SVM分类器之后，对测试数据同样进行分块处理。在均分了测试数据后，从测试数据分块中依次取出数据在各自节点上进行计算，得到3.3小节中的dis，再与给定的阈值ξ进行比较，从而让各节点选择使用SVM算法或使用KNN算法进行分类。所有测试数据分类完成后，对各节点的分类结果进行统一处理和分析。

以上就是SVM_KNN分类算法并行化处理的基本思路，可以将并行化后的SVM_KNN分类算法称之为hSVM_KNN分类算法。根据这个思路，实现hSVM_KNN分类算法需要4对MapReduce函数，分别是迭代训练产生支持向量集、系数w和常数b的函数：IterationMapper函数和IterationReducer函数；求出dis的函数：DisMapper函数和DisReducer函数；SVM分类算法的函数：SVMMapper函数和SVMReducer函数；KNN分类算法的函数：KNNMapper函数和KNNReducer函数。hSVM_KNN分类算法的并行化算法伪代码如下：

FunctionIteration//训练迭代算法

Begin

//将样本训练集分块，放入各节点中处理

Split();

While(不止有一个支持向量集)do

//求出各分块的支持向量集

IterationMapper函数;

//对IterationMapper函数传来的key/value形式的支持向量集两两进行合并处理

IterationReducer函数;

If最后的支持向量集达到迭代精度then

//返回最后的支持向量集Dsv，系数w和常数b

ReturnDsv，w，b;

Else

//如果不满足迭代精度，则进行迭代处理

CallIteration;

Endif

End

FunctionDis//求出dis的函数

Begin

//对测试数据集进行分块，放入各节点中处理

Split_dis();

For分块中的测试数据集D′do

//求得各分块中的dis

DisMapper函数;

//对DisMapper函数传来的key/value形式的dis进行处理

DisReducer函数;

Returndis;

End

Ifdis大于给定的阈值ξthen使用SVM分类算法进行分类;

FunctionSVM//SVM分类算法

Begin

//对dis大于阈值ξ的进行分块，放入各节点处理

Split_SVM();

For分块中的每个disdo

//使用SVM算法进行分类

SVMMapper函数;

//对SVMMapper函数传来的key/value形式的结果进行处理

SVMReducer函数;

End

Ifdis小于给定的阈值ξthen使用KNN分类算法进行分类;

FunctionKNN//KNN分类算法

Begin

//对dis小于阈值ξ的进行分块，放入各节点处理

Split_KNN();

For分块中的每个disdo

//使用KNN算法进行分类

KNNMapper函数(计算距离时加入权重系数对样本进行处理);

//对KNNMapper函数传来的key/value形式的结果进行处理

KNNReducer函数;

End

4 实验结果与分析

为了检验算法的准确性和效率，对算法进行了实验验证。实验选取的数据集是来自UCI数据库中的PokerHand数据集，整个数据集包含11个属性，10个类别和1 025 010个实例，其中训练实例有25 010个，测试实例有1 000 000个。对于多分类的SVM算法，这里采取一对一分类方法[17]，训练10*(10-1)/2=45个SVM分类器。实验中设定惩罚参数C=5，给定阈值ξ=0.6，KNN算法中的K=5。为了使实验结果有效、全面，实验会在测试数据随机抽取的1万、5万、10万、25万、50万、75万、100万个实例上对SVM分类算法和hSVM_KNN分类算法进行比较，对测试数据集多次实验后取平均值作为结果。

图5与图6分别显示了传统的串行SVM算法和hSVM_KNN算法在处理时间和准确性上面的对比。

如图5所示，随着测试实例的数量不断增大，hSVM_KNN算法的处理时间逐渐由劣势变成巨大的优势。当测试实例比较少时，由于hSVM_KNN算法的并行化需要进行传输文件、分配节点和节点之间的通信，这些操作占用了大量时间，所以hSVM_KNN算法在处理时间上要比SVM慢或者接近于相等。当测试实例逐渐增大以后，并行化的优势便体现了出来，传统的SVM算法显然难以适应大型数据的运算，所以处理时间要远远慢于hSVM_KNN算法。

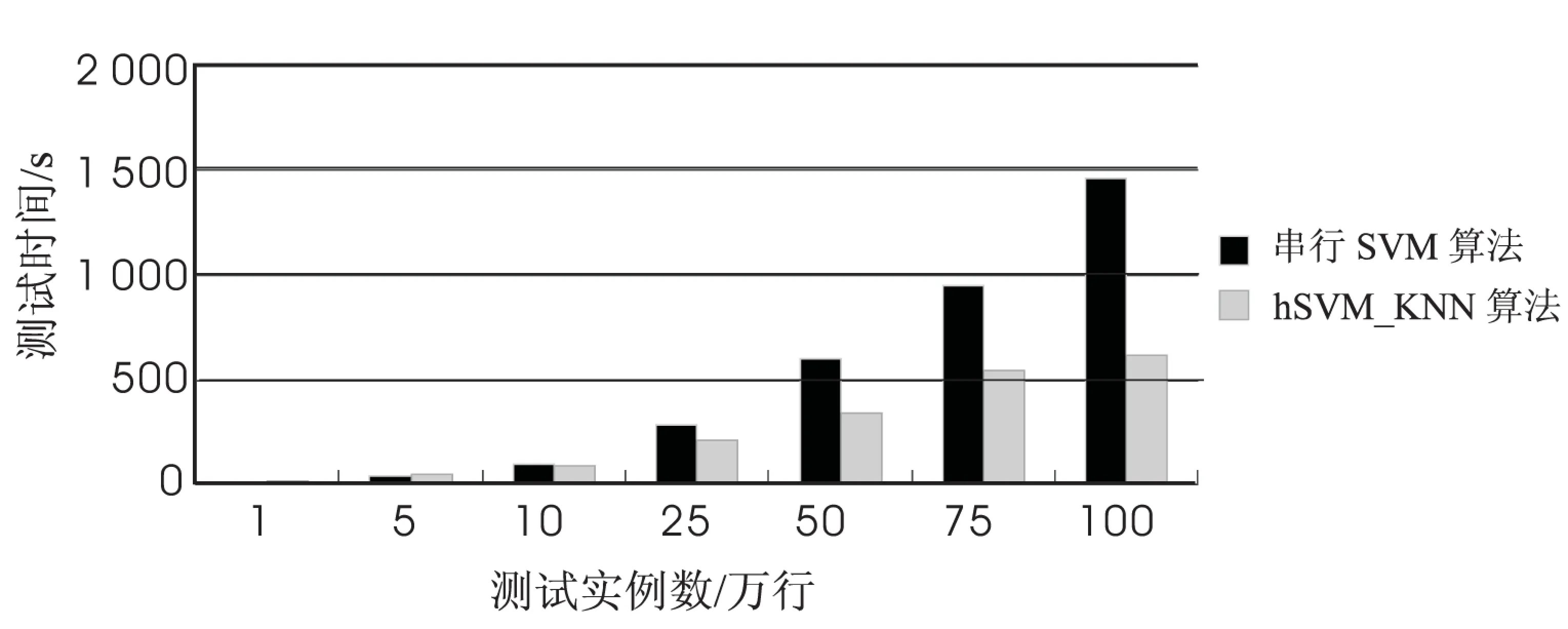
图5 串行SVM与hSVM_KNN算法测试处理时间对比

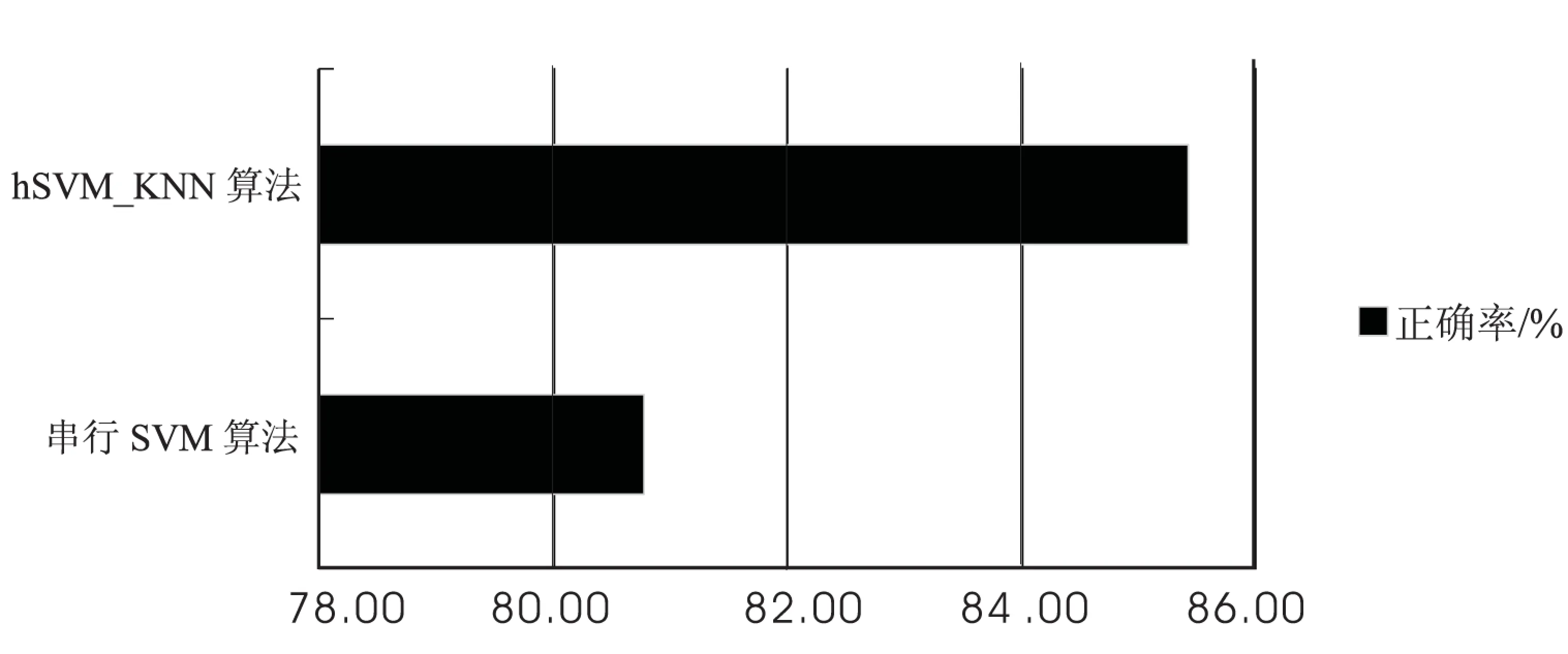
图6 串行SVM与hSVM_KNN准确性对比

从图6可以看出，hSVM_KNN算法在准确性上要高于SVM算法，这是由于hSVM_KNN算法组合了SVM和KNN两种算法，在最优分类面附近的数据分类上比SVM算法有优势，因此hSVM_KNN算法在准确性上也有保证。另外，因为hSVM_KNN算法采用的是并行化处理，所以在处理大数据方面对于每个节点的计算机性能要求也不高，使得算法的成本较低。

5 结束语

文中在分析了SVM算法和KNN算法的优缺点后，将SVM和KNN算法进行结合，形成了一种效率、准确度更高的SVM_KNN算法，对算法进行改进后将其在Hadoop平台上进行并行化处理，得到hSVM_KNN分类算法，从而满足对大数据高速、高效的处理。通过实验可以发现，并行化后的SVM_KNN算法相比于传统的SVM算法在大数据分类的准确性、速度、成本和效率等方面有了明显提升，对核函数的选取也不是很敏感，而且算法的稳定性很好，具有很好的使用价值。

[1] 毛国君,段立娟,王 实,等.数据挖掘原理与算法[M].第2版.北京:清华大学出版社,2007.

[2]BorathakurD.Thehadoopdistributedfilesystem:architectureanddesign[EB/OL].2012-01-20.http://hadoop.apache.org/core/docs/r0.16.4/hdfsdesign.html/.

[3]DeanJ,GhemawatS.MapReduce:simplifieddataprocessingonlargeclusters[J].CommunicationsoftheACM,2008,51(1):107-113.

[4] 武 霞,董增寿,孟晓燕.基于大数据平台hadoop的聚类算法K值优化研究[J].太原科技大学学报,2015,36(2):92-96.

[5] 杨宸铸.基于HADOOP的数据挖掘研究[D].重庆:重庆大学,2010.

[6] 张奕武.基于Hadoop分布式平台的SVM算法优化及应用[D].广州:中山大学,2012.

[7] 王明星.数据挖掘算法优化研究与应用[D].合肥:安徽大学,2014.

[8]AhaDW,KiblerD,AlbertMK.Instance:basedlearningalgorithms[J].MachineLearning,1991,6(1):37-66.

[9] 刘振岩.数据挖掘分类算法的研究与应用[D].北京:首都师范大学,2003.

[10] 郭明玮,赵宇宙,项俊平,等.基于支持向量机的目标检测算法综述[J].控制与决策,2014,29(2):193-200.

[11]PengNanbo,ZhangYanxia,ZhaoYongheng.ASVM-kNNmethodforquasar-starclassification[J].ScienceChina-Physics,Mechanics&Astronomy,2013,56(6):1227-1234.

[12] 章 兢,张小刚.数据挖掘算法及其工程应用[M].北京:机械工业出版社,2006.

[13]CoverT,HartP.Nearestneighborpatternclassification[J].IEEETransonInformationTheory,1967,13(1):21-27.

[14] 侯玉婷,彭进业,郝露微,等.基于KNN的特征自适应加权自然图像分类研究[J].计算机应用研究,2014,31(3):957-960.

[15] 李 蓉,叶世伟,史忠植.SVM-KNN分类器一一种提高SVM分类精度的新方法[J].电子学报,2002,30(5):745-748.

[16] 李丽萍.并行支持向量机[J].计算机光盘软件与应用,2013,24:107-109.

[17]BelUK.Pairwiseclassificationandsupportvectormachines[M].Cambridge,MA:MITPress,1999:255-268.

Research on SVM_KNN Classification Algorithm Based on Hadoop Platform

LI Zheng-jie,HUANG Gang

(School of Computer,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)

The reform of data has brought the unprecedented development,to monitor,analyze,collect,store and apply to the rich and complex structured,semi-structured or unstructured data has become the mainstream of the development of the information age.To classify and deal with the information contained in mass data,it’s needed to have a better solution.The traditional data mining classification method cannot meet the demand any longer.To face these problems,it analyzes and improves the classification algorithm in data mining in this paper.Combined with the algorithms,an improved SVM_KNN classification algorithm is proposed.Then on this basis,by utilizing Hadoop cloud computing platform,the new classification algorithm is put into MapReduce model for parallelization application,so the improved algorithm can be applied to large data processing.Finally,data set is used to conduct experimental verification on the algorithm.By comparing with traditional SVM classification algorithm,the results show that the improved algorithm has become more efficient,fast,accurate and cost-effective,which can effectively carry out large data classification.

data mining;Hadoop;parallelization;SVM_KNN

2015-06-12

2015-09-18

时间：2016-02-18

国家自然科学基金资助项目(61171053)

李正杰(1991-)，男，硕士研究生，研究方向为信息网络与通信软件、海量数据管理；黄 刚，教授，研究生导师，研究方向为计算机在通信中的应用、海量数据管理、移动商务平台设计开发。

http://www.cnki.net/kcms/detail/61.1450.TP.20160218.1630.040.html

TP301.6

A

1673-629X(2016)03-0075-05

10.3969/j.issn.1673-629X.2016.03.