基于压缩感知的鲁棒性说话人识别参数研究
2016-02-23周伟栋
于 云,周伟栋
(南京邮电大学 通信与信息工程学院,江苏 南京 210003)
基于压缩感知的鲁棒性说话人识别参数研究
于 云,周伟栋
(南京邮电大学 通信与信息工程学院,江苏 南京 210003)
奈奎斯特采样下的说话人识别,当为了确保高的识别率而采集较长时间说话人语音时,采样数据量特别大,其中有许多冗余造成了采样资源的浪费,压缩感知理论可以很好地解决此问题。基于压缩感知理论,文中利用行阶梯观测矩阵对信号进行投影,研究了压缩比与识别率的关系,在压缩比为1:2时,保证识别率的同时,使得采样数据量减少为原来的一半。在有噪环境下,将谱减法运用到压缩感知和特征提取过程中,在无需重构时域信号的前提下,直接从已估计的干净语音功率谱中提取具有鲁棒性的特征参数CS-SSMFCC(Compressed Sensing Spectral Subtraction Mel Frequency Cepstral Coefficient)。实验结果表明,与传统的识别参数MFCC(Mel Frequency Cepstral Coefficient)相比,CS-SSMFCC可以有效地提高系统的鲁棒性,具有很好的抗噪性能。
压缩感知;谱减法;特征参数;鲁棒性
0 引 言
说话人识别技术是一种生物认证技术,它从采集到的语音中提取出能够表征话者生理和行为的特征参数来训练模型,在测试时依据提取的特征参数识别说话人身份。常见的生物认证技术有指纹识别、虹膜识别等,比起这些认证技术,说话人识别以其方便性、精确性和经济性越来越受到学者们的关注,并且日益成为重要的安全验证方式[1]。随着社会信息化的逐渐深入和计算机技术的不断发展,说话人识别在不同的领域得到了广泛的应用,用户对其的正确性、鲁棒性的期望也不断提高。
传统的说话人识别包括特征提取、模型训练和模式匹配,其中特征提取是说话人识别的关键,常用的特征有Mel倒谱系数(MFCC)、线性预测系数(LPC)等[2]。在奈奎斯特采样定理下,采样数据量非常多,极大地浪费了采样资源。近年来,压缩感知理论[3-5]很好地解决了此问题。它的核心思想是对信号同时进行压缩和采样,在采样过程中实现了压缩,以远低于奈奎斯特采样率的速率对信号进行采样,获得较少数目的观测序列,进而对观测序列提取特征参数,给说话人识别技术带来了一场新的革命。将压缩感知理论应用于说话人识别的关键是观测矩阵的选取和特征参数的提取,如果经观测矩阵投影后的观测序列保留了原有语音信号的特性,提取的特征会更有意义。而且环境噪声一直是说话人识别性能急速下降的关键因素,在压缩感知框架下提取具有鲁棒性的特征参数也是文中的研究重点。
笔者团队在鲁棒性压缩感知关键技术研究中取得了一定的成果,其中叶蕾[6-7]提出的行阶梯矩阵应用价值可观,经行阶梯观测后的观测序列保留了原有语音信号的特性,给提取特征参数和利用经典消噪方法带来了可能。
文中利用行阶梯观测矩阵得到观测序列,对观测序列提取特征参数,在压缩比为1:2时识别效果很好。在有噪环境下,将谱减法应用于压缩感知和特征提取中,不是从已估计的语音功率谱恢复出时域信号,而是直接对估计的干净语音功率谱提取特征参数,避免了恢复信号的步骤。该方法不仅减少了计算量和复杂度,而且保证了正确性和鲁棒性。
1 压缩感知基本理论
压缩感知主要包括三个方面:信号稀疏表示、观测矩阵和重构算法的设计。假设输入信号x∈RN是一维信号,在某个正交基Ψ∈RN×N上是稀疏的,即
x=Ψα
(1)
式中:α∈RN是稀疏向量,非零项的个数k 对于稀疏信号,利用一个与稀疏基不相关的观测矩阵Φ∈RM×N(M y=Φx=ΦΨα=Acsα (2) 式中:y∈RM是得到的观测序列;Acs是压缩感知(CS)矩阵。 由于M min ||α||1s.t.y=Acsα (3) 最优化方法有基追踪算法BP、贪婪算法OMP[8]等。有些学者已经研究了压缩感知下的说话人识别[9-10],由于文中研究的是在不重构的情况下进行说话人识别,直接对观测序列提取特征参数,所以不需要考虑稀疏基和重构算法的选取。 压缩感知框架下的说话人识别系统分为两个阶段:训练阶段和识别阶段。在训练过程中,对原始语音信号通过观测矩阵得到观测序列,直接对观测序列进行特征提取,将特征参数聚类建立高斯混合模型(GMM)[11]。测试时同样对观测序列提取特征参数,与已建立的模型进行匹配,从而判决说话人的身份。 基于压缩感知的说话人识别系统模型见图1。 图1 基于压缩感知的说话人识别系统模型 将压缩感知与说话人识别相结合,可以大大减少采样点数,减小特征参数的计算量。利用行阶梯矩阵观测原始信号,得到的观测序列保留了原始语音信号大部分特性,进而可以对观测序列利用经典的消噪方法和提取常规的特征参数。目前在干净语音下说话人识别已经发展得相当成熟,然而在有噪环境下识别性能非常不理想,减小噪声的影响已经成为了说话人识别的研究热点[12-13]。压缩感知下的行阶梯矩阵具有一定的消噪能力,因此提取出的特征参数具有鲁棒性。为了进一步减小噪声的影响,将谱减法运用到压缩感知和特征提取中,直接由估计的语音功率谱提取特征,从而得到一种更具鲁棒性的特征参数。 3.1 行阶梯观测矩阵 在压缩感知中,常见的观测矩阵有随机高斯矩阵、部分傅里叶矩阵、随机伯努利矩阵等,但是经过这些矩阵观测后所得的观测序列打乱了原始信号的结构特性,提取的特征参数毫无意义。笔者团队提出的行阶梯矩阵为特征参数的提取提供了可能,文中采用行阶梯矩阵对原始信号进行观测,得到压缩比为r的观测矩阵Φ(r=M/N,即观测序列样点数与原始信号样点数的比值),把m=1/r称作压缩倍数。 (4) 其中,每行1的个数就是压缩倍数m。 如果原始信号为x,经行阶梯矩阵观测后的观测序列为y,则y与x的关系如下: (5) 式中,m=1,2,…,i=1,2,…。 假设压缩倍数m为2,即压缩比r为1:2时,得到原始语音序列和经行阶梯矩阵观测后的观测序列时域波形,如图2所示。发现观测后的序列与原始序列相差无几,保留了原始语音的结构特征,只是幅度变为原来的两倍,频率变快了一倍而已。 图2 一帧语音时域波形比较 图3是一帧语音观测前后的频谱图。一般的特征参数MFCC是基于频谱域提取的,由图可知在采样压缩后的频谱结构几乎没有改变,这为压缩感知框架下的特征提取和消噪方法提供了条件。 图3 一帧语音频谱图比较 假设原始干净信号x混入了噪声e,那么含噪语音表示为: (6) 经过行阶梯矩阵观测得到观测序列: (7) 式中:y是含噪语音观测序列;s是干净语音观测序列;n是噪声观测序列。 应用谱减法的前提条件是噪声是平稳的。假设输入噪声是平稳的,考虑的问题就是经观测后的噪声观测序列是否是平稳信号。根据式(5),假设压缩倍数为2,输入噪声序列e与噪声观测序列n的关系是: ni=e2i-1+e2i (8) 根据随机过程理论,独立的平稳信号之和仍然是平稳信号,因此经行阶梯矩阵观测后的序列依然具有平稳特性。由于白噪声具有平稳特性,选用白噪声作为加性噪声。根据以上分析,将经典的消噪方法—谱减法应用于压缩感知是可行的,给压缩感知框架下的鲁棒性说话人识别技术研究提供了理论依据。 3.2 谱减法 由于环境噪声的影响,训练特征数据集与测试特征数据集发生失配,从而导致识别率急速下降,因此减少噪声的影响一直是说话人识别技术研究的热点。为了解决此问题,语音增强方法被应用到说话人识别中。传统的谱减法作为语音增强方法中的一种,它是基于幅度谱估计和含噪语音的相位恢复出原始干净信号的算法。它可以处理宽带平稳噪声,具有较低的复杂度和较好的消噪效果,已经在语音前端处理中得到了广泛应用。选取Berouti改进后的谱减法[14],基本公式如下: (9) 3.3 基于谱减法的特征提取 传统的特征参数有MFCC,它充分考虑了人耳的听觉特性。在压缩感知框架下,为说话人识别提出了一种新型的特征参数CS-MFCC(Compressed Sensing Mel Frequency Cepstral Coefficient)。该参数在MFCC参数基础上引入了行阶梯矩阵,直接对观测序列提取特征参数,使得特征参数的计算量大大减少。具体过程如下: (1)对采样后的信号加窗分帧,得到语音信号的矩阵形式,选取的帧长是320个点。 (2)利用行阶梯观测矩阵对信号矩阵进行观测,得到维度远小于320的观测序列,观测序列的维度表示压缩后的帧长,压缩比决定了观测序列的维度。 (3)对观测后的每帧语音序列进行离散傅里叶变换,并对其取模的平方得到功率谱。 (4)用Mel滤波器对观测语音序列功率谱进行滤波处理,计算其通过第M个Mel滤波器所得的功率值,得到M个功率值,M是Mel滤波器的个数。 (5)对这M个功率值取对数,得到M个系数。 (6)对M个系数计算其离散余弦变换,即得到CS-MFCC参数。 文中选取的滤波器个数是30,CS-MFCC参数阶数是13。 行阶梯观测矩阵具有消噪的效果,因此提取的CS-MFCC参数具有一定的抗噪性能。但是为了进一步减小噪声的干扰,将谱减法引入到特征参数的提取中。 图4 CS-SSMFCC参数提取过程 采用的语音库来自笔者团队在消音室录制的数据,共有210个说话人,每个说话人180条语句,采样率是16kHz。文中实验选用14个说话人,每个人的5条干净语句用于训练模型,20条语句用于测试。训练时长约30s,每条测试语句长度4~6s不等。添加高斯白噪声在有噪环境下进行实验。在实验过程中,选取的特征参数阶数是13,GMM高斯模型混合度为16。 说话人识别系统性能的好坏可以用识别率来衡量,公式为: (10) (11) 4.1 压缩比与识别率的关系 图5研究压缩比与识别率的关系。帧长固定为320点,即20 ms,压缩倍数(压缩比的倒数)分别取1~10,考察基于压缩感知的说话人识别系统性能。 图5 压缩倍数与识别率的关系 从图中可以看出,压缩倍数越大,识别率越低,压缩倍数的不同意味着观测序列的数目不同,即观测序列的大小对识别性能有影响。固定帧长时,观测序列数目越多,识别性能越好。这也很好理解,观测序列数目越多,就会保留更多的原始语音信号的信息,利于特征参数的提取。然而观测数目太多,计算量会增加。为了权衡采样点数和识别率,选取压缩比为1:2,即观测后的采样序列是以前的一半,此时识别率可以达到96.7%,与未观测前相当。帧长320点,经观测后压缩为160点,MFCC参数提取中仅仅FFT变换这一步需要2 304次乘法,4 608次加法,而CS-MFCC的160点FFT变换只需要1 024次乘法,2 048次加法,计算量大大降低。 4.2 输出信噪比对比 噪声是影响识别率下降的主导因素,在测试语音中添加高斯白噪声进行实验。 表1研究了基于压缩感知和基于压缩感知的谱减法的输出信噪比对比。实验方法是一段语音经过行阶梯矩阵得到观测序列,计算其信噪比,观测序列运用谱减法之后,计算其信噪比。 表1 两种方法输出信噪比对比 从表1可知,随着输入信噪比的增加,输出信噪比也不断提高。行阶梯矩阵具有一定的消噪功能,可以提高输出信噪比。谱减法对观测语音序列起到了增强作用,适用于压缩感知系统中。 4.3 有噪环境下MFCC、CS-MFCC和CS-SSMFCC参数抗噪性能对比 图6比较了在有噪环境下三种特征参数的抗噪性能,实验仿真出不同输入信噪比下识别率的对比。 图6 三种参数下的系统识别率对比 由图可见,随着输入信噪比的提高,识别率都会提升。行阶梯观测矩阵本身具有一定的抗噪效果,所以提取的CS-MFCC参数比传统方法MFCC识别率要高。而文中提取的CS-SSMFCC参数比CS-MFCC抗噪性能好,在较低信噪比下,识别率提高得更加明显。在5 dB和10 dB加性白噪声下,识别率提高了十数量级的百分点。在其他信噪比下,识别率都有不同程度的提升。 文中研究了压缩感知框架下的说话人识别系统,由于一般的随机观测矩阵下的观测序列破坏了原始语音特性,因此文中利用行阶梯矩阵作为观测矩阵,得到的观测序列可以保留原始语音大部分结构特征。对该观测序列提取新型的特征参数CS-MFCC,研究了压缩比对识别性能的影响程度,在压缩比为1:2时,在采样数据量降低的同时,使得识别性能与传统方法相当。为了提高系统的鲁棒性,将谱减法运用到压缩感知理论和特征提取中,直接从已估计的语音功率谱提取具有鲁棒性的特征参数CS-SSMFCC。实验结果表明,与传统参数MFCC相比,CS-SSMFCC可以有效地提高系统的鲁棒性,具有很好的抗噪性能。 [1] 吴昭辉,杨莹春.说话人识别模型与方法[M].北京:清华大学出版社,2009. [2] Kinnunen T,Li H.An overview of text-independent speaker recognition:from features to supervectors[J].Speech Communication,2010,52(1):12-40. [3] Donoho D.Compressed sensing[J].IEEE Trans on Inform Theory,2006,52(4):1289-1306. [4] Candes E J,Romberg J,Tao T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory,2006,52(2):489-509. [5] 石光明,刘丹华,高大化,等.压缩感知理论及其研究进展[J].电子学报,2009,37(5):1070-1081. [6] 叶 蕾,杨 震,王天荆,等.行阶梯观测矩阵、对偶仿射尺度内点重构算法下的语音压缩感知[J].电子学报,2012,40(3):429-434. [7] 叶 蕾,杨 震,孙林慧,等.行阶梯观测矩阵下语音压缩感知观测序列的Volterra+Wiener模型研究[J].信号处理,2013,29(7):816-822. [8] Tropp J A,Gilbert A C.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory,2007,53(12):4655-4666. [9] Griffin A,Karamichali E,Mouchtsris A.Speaker identification using sparsely excited speech signals and compressed sensing[C]//Proc of 18th European signal processing conference.Aalborg,Denmark:[s.n.],2010:1444-1448. [10] 叶 蕾,郭海燕,杨 震.基于压缩感知重构信号的说话人识别系统抗噪方法研究[J].信号处理,2010,26(3):321-326. [11] Reynolds D,Quatieri T F,Dunn R B.Speaker verification using adapted Gaussian mixture models[J].Digital Signal Process,2000,10:19-41. [12] Ming J,Hazen T J,Glass J R,et al.Robust speaker recognition in noisy conditions[J].IEEE Trans on Audio Speech Lang Process,2007,15(5):1711-1723. [13] 何勇军,孙广路,付茂国,等.基于稀疏编码的鲁棒说话人识别[J].数据采集与处理,2014,29(2):198-203. [14] Berouti M,Schwartz R,Makhul J.Enhancement of speech corrupted by acoustic noise[C]//Proc of IEEE international conference on acoustics,speech,and signal processing.Washington:IEEE,1979:208-211. Research on Robust Speaker Recognition Parameters Based on Compressed Sensing YU Yun,ZHOU Wei-dong (College of Communication and Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China) Speaker recognition under Nyquist sampling has got a large amount of data in order to ensure a high recognition rate,resulting in a waste of sampling resources,and compressive sensing theory can solve this problem.Based on compressed sensing theory,it makes use of ladder observation matrix projection in this paper.When the compression ratio is 1:2,the system ensures the recognition rate,so that the sample data is reduced to half.Under noisy environment,spectral subtraction is applied in compressed sensing and feature extraction,and feature parameters are extracted directly from estimated clean speech power spectrum CS-SSMFCC (Compressed Sensing Spectral Subtraction Mel Frequency Cepstral Coefficient).Experimental results show that compared with the traditional identification parameter MFCC (Mel frequency Cepstral Coefficient),CS-SSMFCC based on spectral subtraction under CS framework can effectively improve the robustness of the system,with good anti-noise performance. compressed sensing;spectral subtraction;feature parameters;robustness 2015-06-07 2015-09-15 时间:2016-02-18 国家自然科学基金资助项目(61271335);国家“973”重点基础研究发展计划项目(2011CB302303);江苏省自然科学基金项目(BK20140891) 于 云(1990-),女,硕士研究生,研究方向为说话人识别、语音信号处理。 http://www.cnki.net/kcms/detail/61.1450.TP.20160218.1630.028.html TN912.3 A 1673-629X(2016)03-0018-05 10.3969/j.issn.1673-629X.2016.03.0052 基于压缩感知的系统模型
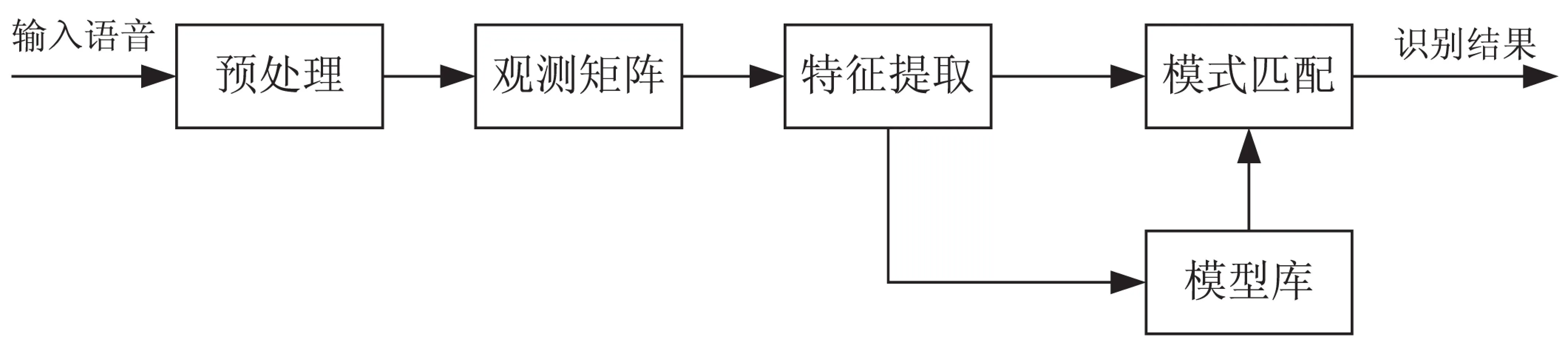
3 有噪环境下基于压缩感知的说话人识别






4 实验结果与分析


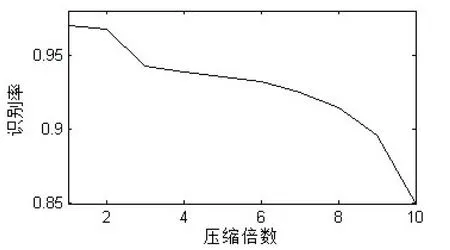

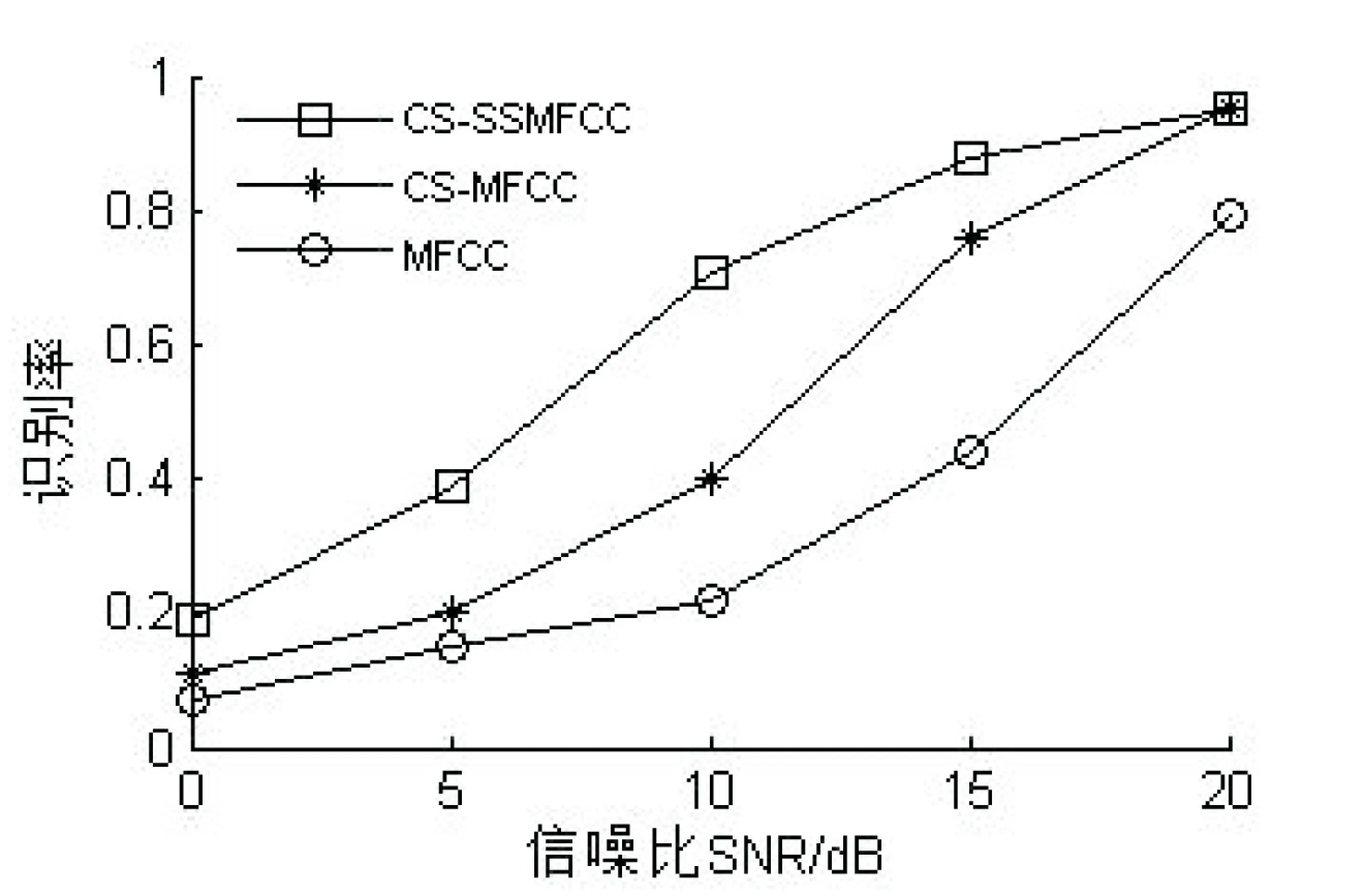
5 结束语
