分式求值有技巧

分式求值有技巧

□华兴恒

分式求值问题是初中数学的重要内容，也是中考的热点.由于分式形式多样，这就要求我们在解答此类问题时，要有灵活的解题策略，这样才能快速、准确地求解.

一、倒数法

再取所求值的倒数，

点评：当已知所求分式的分子是单项式且分母是多项式时，采用取倒数的方法求解常常行之有效.

二、参数法

则有x＝k（a－b）＝ak－bk，y＝bk－ck，z＝ck－ak，

故x＋y＋z＝ak－bk＋bk－ck＋ck－ak＝0.

点评：当已知条件以连比的形式出现，采用设参数的方法求解，很容易找到解题的佳径；有时可根据已知条件求出未知数的比值，再代入所求式来求解，也是不错的选择.

三、拆项法

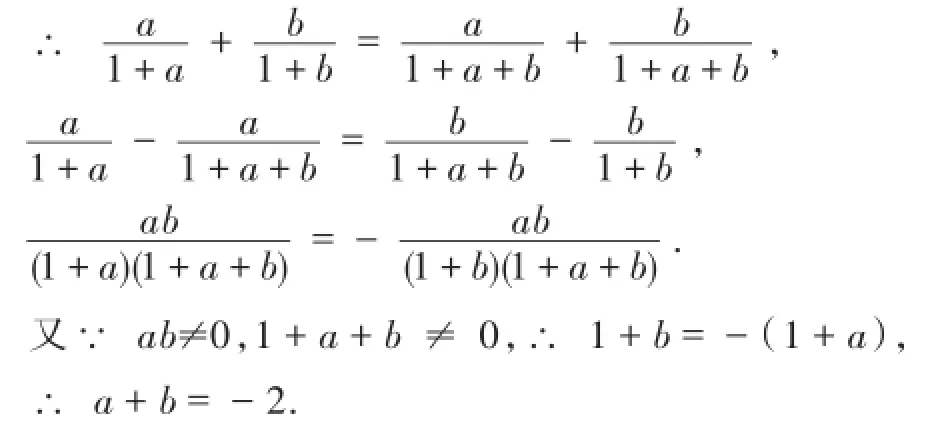
点评：通过巧妙拆分，找到简捷的解题途径，达到快速求解的目的.

四、整体法

例4已知xyz＝1，求的值.

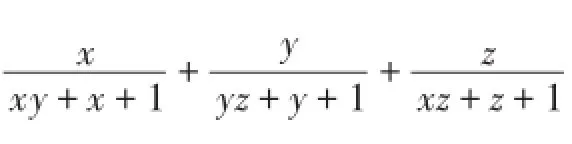
解析：

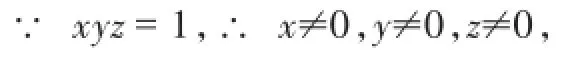
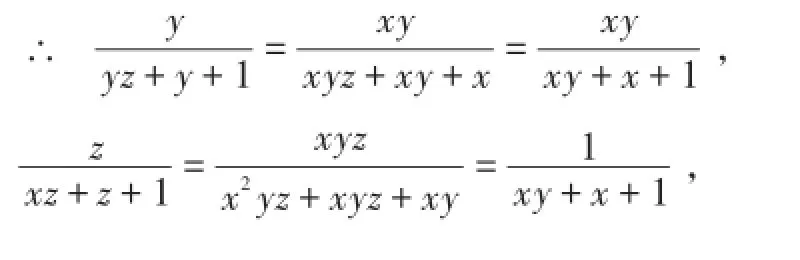
点评：通过把已知条件看做一个整体，再把所求式或所求式的某一部分化为已知整体的代数式，然后代入求解.

五、代入法

解析：由已知条件可得（x2－4x＋4）＋（y2＋6y＋9）＝0，

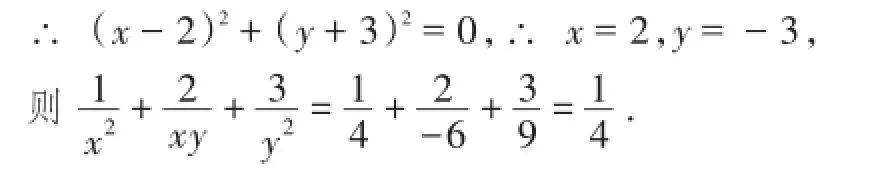
点评：先根据已知条件可直接求出未知数的值，然后再代入求解，较为快速、简便.

六、主元法

点评：当已知条件含有字母的等式的个数比未知字母的个数少时，可将其中一个未知的字母视为已知字母，并用它表示其他未知的字母，然后再代入求解，省时省力.

七、等效法

解析：∵a＋b＋c＝0，∴b＋c＝－a，

∴b2＋2bc＋c2＝a2，∴b2＋c2－a2＝－2bc，

同样可得c2＋a2－b2＝－2ca，a2＋b2－c2＝－2ab.

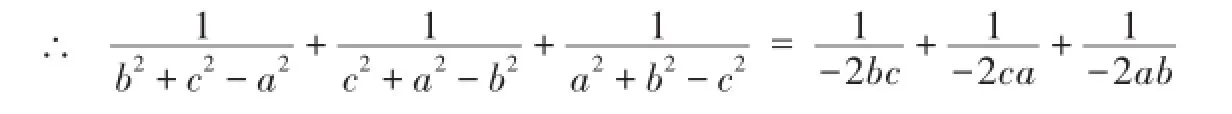
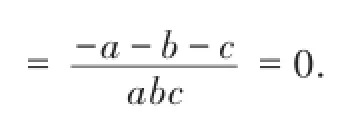
点评：将已知条件和所求式进行适当的变换，将复杂的式子用等效的简单式子代换，然后可顺利获解.

八、拆分法

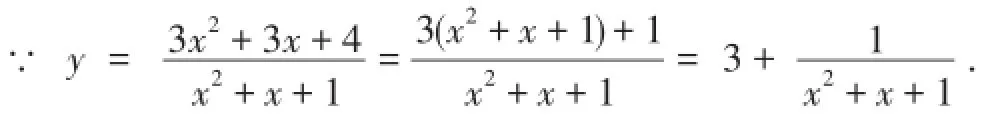
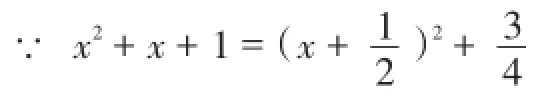
九、换元法

点评：通过换元，将看上去很复杂的问题简单化，可收到事半功倍的效果.