考虑配电可靠性的分布式电源投资策略研究

曾鸣，阿斯卡尔，何科雷，刘伟，王丽华，吕齐

(1.华北电力大学经济与管理学院，北京市 102206; 2.清华大学电机系，北京市 100084)

考虑配电可靠性的分布式电源投资策略研究

曾鸣1，阿斯卡尔1，何科雷1，刘伟1，王丽华1，吕齐2

(1.华北电力大学经济与管理学院，北京市 102206; 2.清华大学电机系，北京市 100084)

合理的分布式电源选址定容可以有效地降低配电网的线路投资和损耗成本，提高含分布式发电的配网系统运行的安全性、可靠性和经济性。结合技术和经济指标，介绍了分布式电源投资的方法，考虑了最优电力潮流(optimal power flow，OPF)、停电成本期望和配电网可靠性，阐述了分布式发电对可靠性指标的影响，并以IEEE-RBTS BUS4的测试系统为例，对各个节点的停电成本、分布式发电容量与配电网可靠性及收益之间的关系进行模拟。研究结果表明，文章提出的分布式电源投资方法，可为投资者选取分布式电源规模和位置提供依据，降低配电网运营成本，提高配电网的供电可靠性。

分布式电源；选址定容；投资；配电系统；可靠性

0 引 言

近年来，由于分布式电源具有运行方式灵活、环境友好等特点以及分布式发电技术的日益发展和应用，分布式电源并网容量不断增加[1]。而随着分布式发电技术的逐步推广，它对配电网中的节点电压、线路潮流、短路电流、可靠性等都会带来影响，且其影响程度与分布式电源的位置和容量密切相关[2-3]。为了充分发挥分布式电源各方面带来的效益，同时使其负面影响最小化，有必要对分布式电源的投资规划进行研究。

国内外对分布式电源投资及其对配电网可靠性影响进行了相关研究。文献[4]分析了分布式电源投资所面临的不确定因素，并提出了3种分布式电源的投资模式。文献[5]提出了不同类型的分布式电源选址定容的长期规划方案，对不同的分布式发电机组规模和位置进行了评估并验证了方法的有效性。文献[6]和文献[7]基于不同类型负荷、分布式电源的时序特性以及不同类型分布式电源的环保性能，建立分布式电源选址定容规划模型，并通过算例验证了所提出模型和方法的可行性和有效性。文献[8]分析了分布式电源的接入对配电网可靠性的影响，建立了考虑分布式电源影响的配电网供电可靠性分析计算模型，通过对一个典型配电网的仿真计算，说明该模型的合理性与有效性。文献[9]指出分布式发电对配电网可靠性既有改善作用，也有不利影响。文献[10]通过系统平均停电时间指数(system average interruption duration index，SAIDI)和系统平均停电频率指标(system average interruption frequency index，SAIFI)评估了配电系统可靠性。文献[11]针对分布式电源与系统电源并列运行情况，提出了一种基于蒙特卡洛方法的分布式电源接入配电系统后的可靠性分析方法。总体看来，目前针对分布式电源选址定容及其对配电可靠性的影响研究较少。鉴于此，本文综合考虑了最优电力潮流(optimal power flow，OPF)和停电成本期望，结合技术和经济指标，提出分布式电源选址定容策略及配电网可靠性评估方法，为分布式电源投资提供参考依据。

1 模型构建

1.1 目标函数

为实现含分布式电源的配电网效益最大化，综合考虑配电网线路升级及维护费用、分布式电源运行总费用以及停电成本，由于电价和燃料价格具有不确定性，使用蒙特卡洛模拟计算成本期望[12]，通过使总成本最小化，确定最佳分布式电源位置及规模。因此，目标函数表达式为

minEComg+ECcut

(1)

式中：EComg为配电网营运及维护成本和分布式发电成本总和的期望值；ECcut为停电成本期望。

1.2 最优电力潮流

一般在电力系统经济调度运行中的最优潮流计算是以运行成本最小化为目标[13]。整个系统发电燃料总消耗量可通过式(2)计算。

(2)

式中：N为系统所有发电机的集合，平衡节点为s；KGi为发电机组Gi耗量特性。

平衡节点s的有功出力为非控制变量，通过潮流计算决定其注入功率，注入功率为节点相角θ和电压幅值U的函数，因此

PGs=Ps(U,θ)+PLs

(3)

式中：Ps(U,θ)为与节点s相关的线路输出的有功功率；PLs为节点s负荷功率。

1.2.1 约束条件

(1)总线电压约束为

(4)

(2)基本潮流方程约束为

(5)

(6)

式中：θij=θi-θj(i≠j)；Gij和Bij分别为节点导纳矩阵第i行第j列约束的实部和虚部。

(3)发电机组有功出力和无功出力约束为

(7)

(8)

(4)输电线路容量约束为

(9)

1.2.2 节点边际电价模型

节点边际电价指特定总线每增加一单位电能供应时的边际成本。节点边际电价通常由边际能源价格、边际耗损价格和边际阻塞费用3部分组成。考虑总线的实际电价，则主网总线在第i个h的节点边际电价为

λLMPi=λ+λLi+λCi

(10)

式中：λ为参考总线的边际能源价格，所有的总线路的边际能源价格均相等；λLi为边际耗损费用；λCi为边际阻塞费用。由于耗损费用和阻塞费用不同，因此每条总线路的电价均不同。

1.3 分布式发电成本

分布式发电成本包括设备费、运行和维修成本、燃料费等。其中，运行和维修成本由固定部分和变动部分组成。固定的运行维修成本主要包括车间操作人工费，运行维修成本的变动部分主要由周期性的系统组件的检查、更换和修理费用构成。

在寿命周期内，以Clife表示分布式发电投资的生命周期成本，计算公式为

(11)

式中：Cc为每年建设投资成本；CO&M为每年的运行和维护成本；CL为贷款支付部分；rd为市场折现率；rL为贷款利率；Nc为建设周期；NL为贷款年限，N为系统寿命年限。

以Cyear表示年成本平均费用，则年平均费用Cyear可通过寿命周期成本Clife乘以等额分付资本回收系数得到，表达式为

(12)

分布式发电项目每年总成本等于年平均费用加上年燃料费，表达式为

CDG=Cyear+Cfuel

(13)

当前，分布式电源主要有光伏发电、风力发电、燃气轮机发电和燃料电池等。由于光伏发电和风力发电均为可再生能源，故燃料成本为0；微型燃气轮机与燃料电池所用燃料均为天然气，年燃料成本计算表达式为

(14)

式中：Cnl为微型燃气轮机使用的天然气价格，元/m3；Vnl为天然气的低热值，kWh/m3；Pi为第i个h的平均净输出功率，kW；ηi为在第i个h的内微型燃气轮机的(燃料电池)平均效率。

能源成本Comg为配电网营运及维护成本和分布式发电成本之和，表达式为

(15)

式中：λLMPi为主网总线在第i个h的节点边际电价；Pi在第i个h的配电网消耗功率。

分布式发电容量和每年预期停电成本、能源成本、分布式发电成本和总成本之间的关系如图1所示。可见，存在最优分布式发电容量A，使配电网总成本最低。

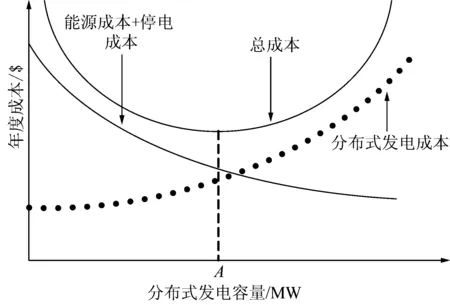
图1 分布式发电容量和成本关系图Fig.1 Relationship between distributed generation capacity and cost

1.4 分布式发电选址定容

可通过如下步骤确定最优分布式电源规模和位置，使总成本最小化。

(1)确定配电网中安装分布式发电设备的候选节点。

(2)在候选节点安装分布式发电设备后，运用最优电力潮流技术确定在配电网中供电总线路的节点边际电价。

(3)依据用户的类型和停电的持续时间和范围，计算出每位用户的停电成本。

(4)确定每个负荷点中断时间，然后根据所有负荷点的预期停电成本总和，获取配电网中每个分布式发电候选位置的预期停电成本。

(5)计算每个节点电价和燃气价格成本，确定安装分布式发电设备的候选位置。

(6)计算每个分布式发电候选位置的期望年能源成本。

(7)计算目标函数的值。

(8)选出目标函数值最小的分布式发电的规模和位置。

(9)如果目标函数下降则对下一个分布式发电的规模位置重复5—8步骤。

1.5 配电网可靠性评估

配电系统可靠性评估通过可靠性指标来体现。基本配电系统可靠性指标为3个负荷点指标：(1)负荷端平均故障率δ，次/年；(2)平均停机持续时间ζ，h/次；(3)年平均停电时间τ，h/年。

(16)

(17)

τ=δ·ζ

(18)

通过3个基本负荷点指标计算电力不足期望值EENS的可靠性成本价值指数、停电成本期望ECcut和停电损失评价率RIEA，分析可靠性数据指标，进一步总结归纳出分布式发电对供电可靠性的影响。本文考虑的可靠性指标有：

(1)系统平均停电时间TSAIDI。计算表达式为

(19)

(2)电量不足期望值EENS。计算表达式为

(20)

(3)停电成本期望ECcut。每个负荷点的停电成本期望取决于用户类型和停电持续时间。计算表达式为

(21)

(4)停电损失评价率RIEA。计算表达式为

(22)式中：Ni为受持续停电影响的用户数量；Ui为负荷点i的等值年平均停电时间；Np为负荷点的总体数量；Ne为配电网中电极元件的总数量；φ为用户损失函数。

2 算例分析

本文以IEEE-RBTS测试系统BUS4的配电系统为例。文献[14]叙述了整个系统和负荷数据并给出了该系统的基本可靠性参数。假定组件的维修时间服从对数正态分布，标准差为平均值的1/3，组件的故障时间服从指数分布。RBTS测试系统规定了每条母线的用户类型、总峰值负荷。系统包括了38个负荷点和3种用户类型，居民用户、商业用户和工业用户。每种用户类型的平均停电损失费用如表1所示。

表1 用户停电损失费用
Table 1 Interruption cost of users

此配电网有27个安装分布式发电设备的候选节点，如图2所示。本系统中使用微型燃气涡轮发电机。

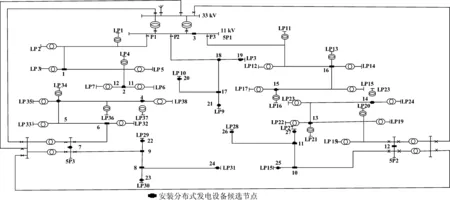
图2 RBTS BUS 4配电系统Fig.2 Distribution system for RBTS Bus 4

假定所有的分布式发电机组功率因数为0.8，资本成本为1 000$/kW，表2列出了财务分析所需的相关参数。

表2 财务分析相关参数
Table 2 Relevant parameters of financial analysis

当分布式发电连接到配电网后，应用提出的评估可靠性指标和总运营成本的方法可得到不同的结果。分布式发电候选节点的停电成本期望和能源成本期望模拟结果如图3所示。

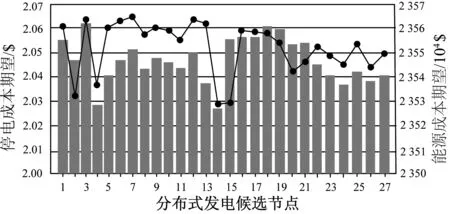
可见，当分布式电源安装在节点14时，停电成本期望ECcut降低程度最大，安装在节点4时，能源成本期望EComg降低程度最大。通过计算比较节点4与节点14的目标函数值，得出节点14为安装分布式电源的最佳位置。

安装分布式发电设备容量和收益之间的关系如图4所示。

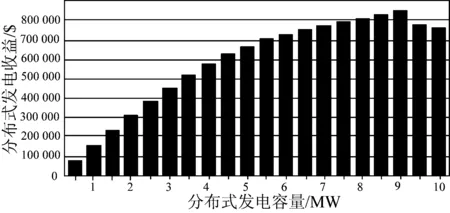
图4 分布式发电容量及收益Fig.4 Capacity and revenue of distributed generation

在配电系统中安装分布式发电设备会影响可靠性指标。根据公式(19)、(20)、(22)计算分布式发电对配电系统中平均停电时间TSAIDI、电量不足期望值EENS和停电损失评价率RIEA的影响，如图5和图6所示。

图5 系统平均停电时间指标Fig.5 System average interruption duration index

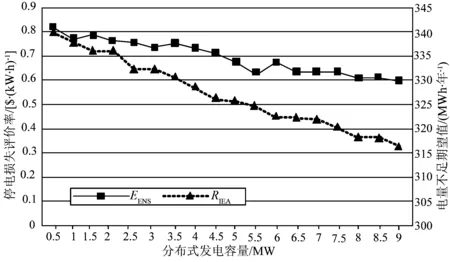
图6 停电损失评价率和电量不足期望值Fig.6 Interruption loss rate and expected energy not supplied

由图5以及图6可以看出，当分布式发电容量为9 MW时，平均停电时间TSAIDI、电量不足期望值EENS和停电损失评价率RIEA均达到最小。结合停电成本期望ECcut和能源成本期望EComg分析结果，在节点14安装容量为9 MW的分布式电源时，年运营总成本最小，效益最大。

3 结 论

分布式电源对配电网具有重要影响，合理的分布式电源规模及位置可以减少配电系统总的运营成本。本文考虑了最优电力潮流、用户停电成本提出了考虑配电系统可靠性分布式电源投资策略，通过算例分析表明：(1)用户类型及停电成本会对配电网可靠性指标产生影响；(2)考虑最优电力潮流、用户停电成本的分布式电源投资策略有利于更加合理地选取分布式电源规模和位置，提高分布式发电收益，降低配电网运营成本，提高配电网的供电可靠性。

[1]隋礼辉.基于TOPSIS法与灰色关联度的分布式电源投资效益分析[J].水电能源科学，2012，30(7)：194-196，184. SUI Lihui. Investment benefits analysis of distributed generation based on TOPSIS and grey correlation degree [J]. Water Resources and Power, 2012, 30(7): 194-196, 184.

[2]芦晶晶，赵渊，赵勇帅，等.含分布式电源配电网可靠性评估的点估计法[J].电网技术，2013，37(8)：2250-2257. LU Jingjing, ZHAO Yuan, ZHAO Yongshuai, et al. A point estimation method for reliability evaluation of distribution network with distributed generation [J]. Power System Technology, 2013, 37(8): 2250-2257.

[3]叶萌，刘文霞，张鑫.考虑电压质量的分布式电源选址定容[J].现代电力，2010，27(4)：30-34. YE Meng, LIU Wenxia, ZHANG Xin. Locating and sizing of distributed generation for improved voltage quality [J]. Modern Electric Power, 2010, 27(4): 30-34.

[4]曾鸣，赵建华，刘宏志，等.基于区间数的分布式电源投资效益分析[J].电力自动化设备，2012，32(8)：22-26, 34. ZENG Ming, ZHAO Jianhua, LIU Hongzhi, et al. Investment benefit analysis based on interval number for distributed generation[J]. Electric Power Automation Equipment, 2012, 32(8): 22-26, 34.

[5]KARIMYAN P， GHAREHPETIAN G B， ABEDI M，et al.Long term scheduling for optimal allocation and sizing of DG unit considering load variations and DG type[J].International Journal of Electrical Power & Energy Systems, 2014, 54: 277-287.

[6]李亮，唐巍，白牧可，等.考虑时序特性的多目标分布式电源选址定容规划[J].电力系统自动化，2013，37(3)：58-63, 128. LI Liang, TANG Wei, BAI Muke, et al. Multi-objective locating and sizing of distributed generators based on time-sequence characteristics[J]. Automation of Electric Power Systems, 2013, 37(3): 58-63, 128.

[7]徐迅，陈楷，龙禹，等.考虑环境成本和时序特性的微网多类型分布式电源选址定容规划[J].电网技术，2013，37(4)：914-921. XU Xun, CHEN Kai, LONG Yu, et al. Optimal site selection and capacity determination of multi-types of distributed generation in microgrid considering environment cost and timing characteristics[J]. Power System Technology, 2013, 37(4): 914-921.

[8]施伟国，宋平，刘传铨.计及分布式电源的配电网供电可靠性研究[J].华东电力，2007，35(7)：37-41. SHI Weiguo, SONG Ping, LIU Chuanquan. Power supply reliability of distribution network including distributed generation [J]. East China Electric Power, 2007, 35(7): 37-41.

[9]雷振，韦钢，蔡阳，等.含分布式电源区域节点的配电网模型和可靠性计算[J].电力系统自动化，2011，35(1)：39-43, 76. LEI Zhen, WEI Gang, CAI Yang, et al. Model and reliability calculation of distribution network with zone-nodes including distributed generation [J]. Automation of Electric Power Systems, 2011, 35(1): 39-43, 76.

[10]Al-MUHAINI M, HEYDT G T, HUYNH A. The reliability of power distribution systems as calculated using system theoretic concepts[C]//Power and Energy Society General Meeting，2010 IEEE, Minneapolis, MN: IEEE, 2010: 1-8.

[11]袁兆祥，孔祥玉，赵帅.分布式电源接入配电系统可靠性分析方法[J].电力系统及自动化学报，2013，25(4)：112-116. YUAN Zhaoxiang, KONG Xiangyu, ZHAO Shuai. Reliability analysis method for distribution system with distributed generation [J]. Proceedings of the CSU-EPSA, 2013, 25(4): 112-116.

[12]骆珣，贾建容.基于蒙特卡洛模拟的火电建设项目投资风险估计[J].北京工商大学学报 (自然科学版)，2006，24(3)：66-68. LUO Xun, JIA Jianrong. Risk evaluation of investment decision making in thermal power construction project based on Monte Carlo simulation [J]. Journal of Beijing Technology and Business University (Natural Science Edition), 2006, 24(3): 66-68.

[13]吴伟丽，李小明.基于发电成本最低的最优潮流算法及其可视化展示[J].新疆大学学报(自然科学版)，2012，29(3)：358-362. WU Weili, LI Xiaoming. Application of power simulator in the optimal power flow [J]. Journal of Xinjiang University (Natural Science Edition), 2012, 29(3): 358-362.

[14]ALLAN R N，BILLINTON R，SJARIEF I, et al. A reliability test system for educational purpose-basic distribution system data and results[J]. IEEE Transactions on Power Systems，1991, 6(2): 813-830.

吕齐(1994)， 男，本科，主要从事电力技术经济方面的研究工作。

(实习编辑 景贺峰)

Distributed Generation Investment Strategy Considering Distribution System Reliability

ZENG Ming1, A Sikaer1, HE Kelei1, LIU Wei1, WANG Lihua1， LYU Qi2

(1.School of Economics and Management, North China Electric Power University, Beijing 102206, China;2.Department of Electrical Engineering, Tsinghua University, Beijing 100084, China)

The line investment and loss cost of distribution network can be effectively reduced and the security, reliability and economy of distribution network system operation can be improved with reasonable locating and sizing distributed power. Considering the optimal power flow (OPF), the expectation of interruption cost and the reliability of distribution network, we introduce the investment method of distributed power with the combination of technical and economic indicators, and discuss the effect of distributed generation on the reliability index. Then, we simulate the relationship between the interruption cost of each node, distributed generation capacity, distribution network reliability and revenue with taking an IEEE-RBTS BUS4 test system as example. The research results show that the proposed investment method of distributed generation can provide the basis for investors to select the size and location of distributed generation, reduce the operating cost of distribution network and improve its power supply reliability.

distributed generation; locating and sizing; investment; distribution system; reliability

国家自然科学基金项目(71271082)

F 416.61

A

1000-7229(2016)03-0052-06

10.3969/j.issn.1000-7229.2016.03.008

2015-11-15

曾鸣(1957)，男，教授，博士生导师，主要从事电力系统投资规划、电力市场理论、需求侧管理方面的研究工作；

阿斯卡尔(1963)，男，博士研究生，主要从事电力系统投资规划方面的研究工作；

何科雷(1990)，男，硕士研究生，主要从事电力系统投资规划方面的研究工作；

刘伟(1992)，男，硕士研究生，主要从事电力技术经济分析方面的研究工作；

王丽华(1990)，女，硕士研究生，主要从事电力技术经济分析方面的研究工作；

Project supported by National Natural Science Foundation of China (71271082)