解列后电力孤岛的校正控制策略研究

宋洪磊，李晓飞，吴俊勇，胡佳琳，王振明

(1.国家电网公司交流建设分公司，北京市 100052；2.国网电力科学研究院，南京市 211006；3.北京交通大学电气工程学院，北京市 100044；4.华北电力大学电气与电子工程学院，北京市 102206 )

解列后电力孤岛的校正控制策略研究

宋洪磊1，李晓飞2，吴俊勇3，胡佳琳4，王振明1

(1.国家电网公司交流建设分公司，北京市 100052；2.国网电力科学研究院，南京市 211006；3.北京交通大学电气工程学院，北京市 100044；4.华北电力大学电气与电子工程学院，北京市 102206 )

当失稳系统实施主动解列控制后，被分割成独立的2个或者2个以上的不稳定电力孤岛，此时，必须快速采取有效的校正控制措施，保证各个电力孤岛稳定运行。提出了基于解列断面双向潮流跟踪算法和直流潮流算法的电力孤岛快速实时校正控制策略。通过对解列断面潮流进行追踪，得到孤岛内的调整对象(发电机和负荷)和调整量，再利用直流潮流算法进行校验，使得各孤岛在满足安全稳定约束条件下保持暂态稳定。通过新英格兰39节点系统验证了所述方法的有效性和适应性。

解列孤岛；校正控制；潮流跟踪算法；直流潮流算法；切机切负荷

0 引 言

随着我国特高压电网的发展和大区域互联电网的形成，电力系统的安全稳定面临着严峻的挑战。当大型互联电网遭受严重故障时，需要采取主动解列控制措施来避免事故蔓延或电网崩溃[1-4]。特别是在特高压交流联络线解列后，各个孤岛内的发电机和负荷间存在不平衡功率，使得线路可能越限运行，此时，应当快速采取有效的稳定控制措施，保证各个电力孤岛能独立稳定运行。例如2012年7月30日和31日，印度发生了世界范围内影响人口最多的大规模停电事故，其中北部、东部和东北部3个互联的区域电网因功角、频率和电压失稳导致崩溃，而西部电网通过与北部和东部电网解列形成孤岛电网，并采取有效控制措施而免于发生大范围停电事故[5]。所以解列后孤岛内的实时校正控制对加强和健全电网第3道防线具有重大理论和实际意义[6]。

解列后孤岛的稳定控制是通过切机切负荷措施实现的[7-9]。文献[10-12]提出了考虑负荷频率特性的切负荷策略，保证了系统的安全稳定。文献[13]综合考虑反映系统功角稳定和频率稳定的数学模型，建立了暂态稳定的切机切负荷控制模型，通过线性化方法大大减少了计算量，并保证了求解的准确性。文献[14]将复杂网络与电力系统的物理实际相结合，提出了一种用于暂态功角稳定的切机控制策略计算方法，并通过评价指标确定最佳的切机地点和切机量。文献[15]提出了一种紧急控制下基于快速时域仿真的最优切机切负荷算法，在考虑切机切负荷量的同时还需要考虑最优控制时间[16]。

可以看出，在以往的研究中主要是针对孤岛的频率不稳定而采取的切机切负荷控制措施，对于大互联系统发生失稳后利用主动解列措施对各不稳定孤岛进行稳定控制的研究相对较少。本文对失稳系统实施主动解列控制后电力孤岛的校正控制措施进行研究，提出一种电力孤岛校正控制策略的快速求取方法。该方法可以得到孤岛内最优切机切负荷量，确保主动解列控制的稳定性。

首先分析解列断面支路对发电机和负荷功率的灵敏度，基于解列断面各支路的双向潮流跟踪算法确定孤岛内的调整对象(发电机和负荷)和调整量。再利用直流潮流算法对电力孤岛实施切机切负荷控制后的功率平衡和支路潮流进行校验，最后得到能保证电力孤岛稳定运行的最优切机切负荷量，从而确保各个电力孤岛稳定可靠运行，并确保主动解列控制的稳定性。

1 基于双向潮流跟踪法的解列断面功率追踪

1.1 双向潮流跟踪算法

根据支路潮流的运行方向，功率跟踪算法可以分为顺流跟踪算法和逆流跟踪算法。基于潮流跟踪算法的思路，对线路中的越限支路可以向发电机和负荷进行双向潮流跟踪，得到该支路功率在相关发电机和负荷中的功率分配情况。

如图1所示，假设系统中某一条联络线路为Lij，其功率从节点i流向节点j。与线路的2个节点相连的线路集表示为Ω，对于线路的每一个节点都是由注入功率和流出功率2部分线路组成，这里定义线路两侧节点的连接线集合为

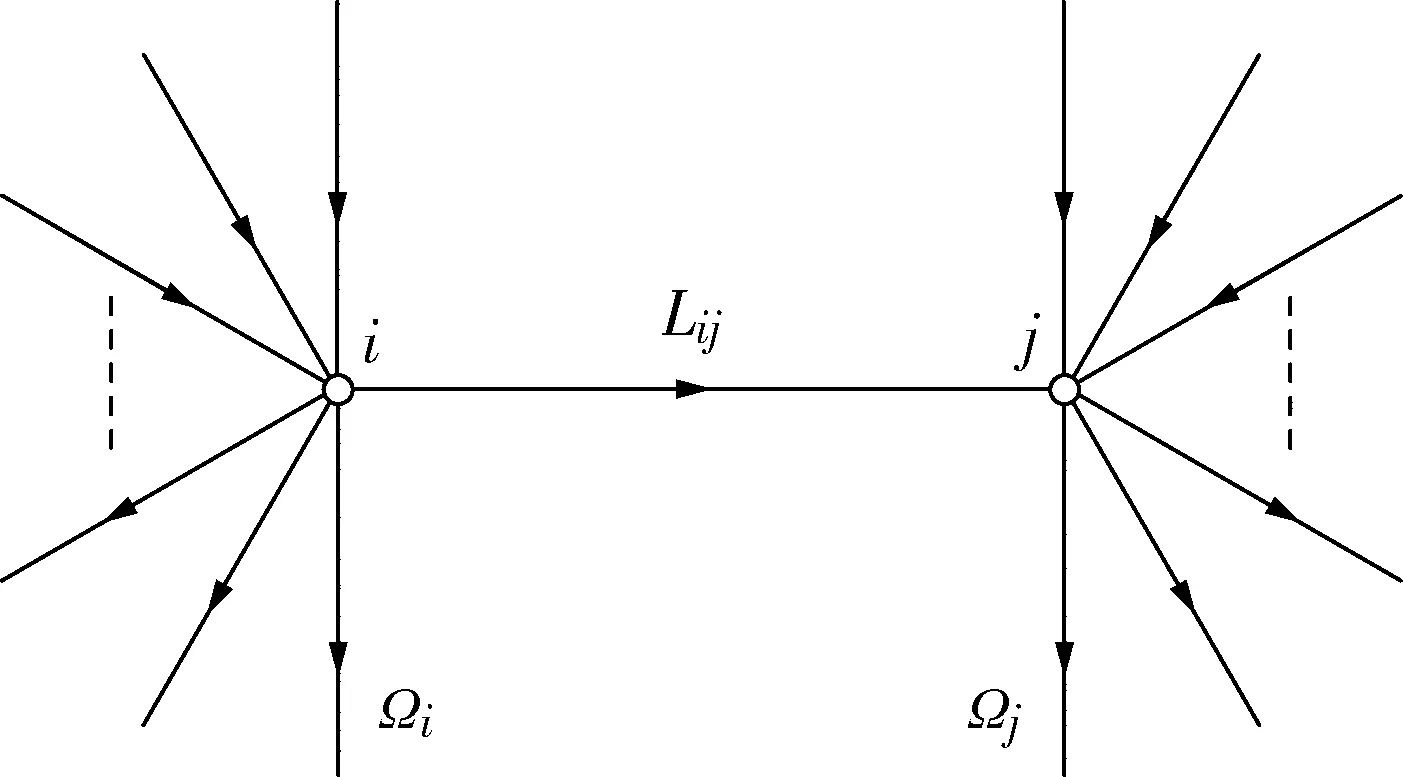
图1 支路潮流的双向跟踪示意图Fig.1 Bidirectional tracing of transmission line power flow

(1)

对于线路Lij的潮流功率，假设支路潮流注入节点方向为正方向，流出节点方向为反方向，则功率向量表示为

(2)

基于基尔霍夫节点定理，对于线路节点i和节点j，注入、流出的功率和为0，从图1中可看出，节点i和节点j中既有注入功率，也有流出功率，所以对于每个节点的功率都可以分成注入集和流出集，表示为

(3)

根据支路线路2个连接节点的潮流分布，通过向发电机和负荷进行双向潮流跟踪，便可得到影响该支路功率的调整对象和调整量。

1.2 解列断面功率的潮流追踪算法

假设得到解列断面的所有线路集合为S={L1,L2,…,Ln}，由于一组解列断面中存在功率潮流方向不同的线路，若规定从电力孤岛1流入孤岛2的支路潮流方向为正方向，则从电力孤岛2流入孤岛1的支路潮流方向为反方向。则可以得到解列断面支路的线路集合和相应支路的功率值：

S=Sa+Sb={L1,L2,…,Lk}+{Lk+1,Lk+2,…,Ln}

(4)

(5)

式中：Sa、Sb分别表示正、反方向潮流的线路集合；Pa、Pb分别表示正、反方向潮流支路的功率值。

对于发电机功率大于负荷功率的电力孤岛，需要实施切机措施来保证孤岛系统的功率平衡。对断面的每条线路进行逆向潮流跟踪直到全部发电机节点，可以得到需要调整的发电机调整量为：

GS={G1,G2,…,GMG}

(6)

PG-S={PG1,PG2,…,PGMG}

(7)

式中：GS表示需要调整的发电机的集合；PG-S表示需要调整的发电机所发出功率的集合；MG表示在电力孤岛中与断面线路相关的发电机数量；PGi表示经过该断面的由发电机Gi发出的功率。

对于负荷功率大于发电机功率的电力孤岛，需要实施切负荷措施来保证孤岛系统的功率平衡。对断面的每条线路进行顺向潮流跟踪直到全部的负荷节点，得到负荷节点调整量为：

LS={L1,L2,…,LNL}

(8)

PL-S={PL1,PL2,…,PLNL}

(9)

式中：LS表示需要调整的负荷集合；PL-S表示需要调整负荷所消耗的功率集合；NL表示在电力孤岛中与断面线路相关的负荷节点的数量；PLi表示经过该断面的由负荷Li所消耗的功率。

所以，对于构成解列断面的每一条潮流线路，在解列后的各个功率不平衡的孤岛中可以得到需要采取控制措施的发电机或负荷节点，并利用双向潮流跟踪算法将不平衡量在各孤岛内的发电机和负荷间进行分配，得到各个电力孤岛内需要调整的对象和调整量，通过切机切负荷控制来保证孤岛内的功率平衡。

2 基于直流潮流算法的快速切机切负荷控制策略

2.1 线路有功功率对发电机和负荷的灵敏度分析

线路有功功率对发电机和负荷的灵敏度分析主要包含解列断面支路对孤岛内发电机和负荷调整对象和调整量的初始确定，以及解列后形成的各孤岛内越限支路对发电机或负荷的灵敏度，并依此进行调整，保证孤岛能够稳定运行。

2.2 电力孤岛的直流潮流算法分析

虽然交流潮流计算精度较高，但是计算量大，耗费时间较长，不满足计算快速和收敛可靠的要求。直流潮流计算是将非线性问题简化为线性问题，无须迭代使计算大为简化，比较适用于输电系统规划和运行方式制定时大量的过负荷检验[19]。

对于电力网络中的任一支路L(i,j)，若忽略其并联支路，则支路的潮流方程可以表示为

(10)

式中:Ui、Uj分别表示节点i、j的电压；θij表示支路L(i,j)首末两端的电压相角差；gij表示支路电导；bij表示支路电纳。

电力系统在正常运行时，其节点电压在额定电压附近，并且支路两端相角差很小，而对超高压电力网，线路电阻比电抗小得多。因此，做如下假设简化潮流方程：

(1) 由于各节点电压的标么值都在额定电压附近，所以假设各节点电压的标幺值约等于1；

(2) 对于超高压电力线路，线路电阻比电抗小的多，所以假设电阻约等于0，可以在潮流计算中忽略电力线路的有功功率损耗；

(3) 输电支路两侧的电压相角差很小，可以假设sinθij≈θij，cosθij≈1，并且不考虑接地支路及变压器非标准变比。

则公式(10)可以化简为

(11)

转化为矩阵形式可以表示为

P=Bθ

(12)

式中：P表示各支路有功功率的向量；B表示各支路导纳矩阵组成的对角矩阵；θ表示各支路两端的相角差向量。

相当于在交流电网中把节点的注入功率看作直流电路中节点的注入电流，节点电压的相角看作直流电路中的电压，从而利用直流潮流方法可以快速计算判断解列后各个电力孤岛的支路功率是否越限。

利用直流潮流算法对每一条支路的有功功率进行校验，检验其是否满足最大输送功率约束。因为直流潮流算法不能充分考虑孤岛内的无功功率和电压，所以还需要再结合PQ分解潮流算法对满足有功约束的线路进行无功和电压校验，即对孤岛内的无功功率进行平衡调整，最后确定孤岛内切机切负荷的调整量。在PQ分解潮流算法中，无功功率的平衡调整可以根据与有功功率间的比例关系确定：

(13)

式中： ΔQ表示无功功率的调整量；Q0表示直流潮流算法得到的无功功率；P0表示直流潮流算法得到的有功功率；ΔP表示有功功率的调整量。

2.3 孤岛内实时校正控制策略流程

本文提出的电力孤岛内实时校正控制策略是基于解列线路双向潮流追踪算法和直流潮流算法实现的。通过对解列线路的双向潮流追踪确定各个电力孤岛内需要调整的发电机或负荷调整对象及调整量；再利用快速的直流潮流算法对切机或切负荷后的电力孤岛系统中的线路进行越限校验，并结合PQ分解潮流算法对影响孤岛稳定运行的节点电压进行进一步验证。具体实施的细节和流程如下。

(1) 调整对象的确定。利用解列断面支路对于各孤岛内发电机或负荷的灵敏度和双向潮流跟踪算法确定各孤岛内的调整对象和调整量，将不平衡功率在各孤岛内进行分配。

(2) 控制量的确定。利用直流潮流算法对初始得到的控制量进行线路传输潮流越限校验和修正，通过直流潮流和PQ分解潮流算法确定控制量。

假设利用解列支路的双向潮流跟踪算法得到需要切除负荷的地点和负荷量矩阵为ΔPLm(m=1,2,…,k)，在孤岛系统内发电机节点的功率定义为PG，其他节点(包括非发电机节点、非负荷节点以及不需要切除的负荷节点)的功率为Pelse，利用直流潮流算法得到孤岛系统内各节点的电压相角：

(14)

便可以得到切负荷控制后传输线路的功率Pij=Bijθij(i=1,2,…,n;j≠i)，对传输线路的有功功率进行越限验证，如果线路不越限，结合公式(13)对孤岛系统内线路的无功功率进行调整，利用PQ分解潮流算法对节点电压进行验证；如果线路越限，调整发电机或负荷的控制量继续计算直流潮流。最终得到孤岛系统内需要控制的对象和相应的调整量。

(3) 控制顺序的确定。对每一条解列支路所形成的孤岛内的每一个发电机和负荷的有功功率进行灵敏度分析，并对其进行排序，便可以得到解列的支路集对于孤岛内的发电机和负荷功率的灵敏度解析式，根据灵敏度大小顺序进行控制。

根据上述控制步骤，得到孤岛区域内的实时校正控制流程如图2所示。

3 算例分析

本文以新英格兰39节点系统作为算例，验证本算法提出的合理性和有效性。根据文献[20]中的算例，在线路6—7处发生三相瞬时短路故障，导致31号和32号发电机失稳，得到最佳解列断面为支路8—9，4—3，14—15。2个孤岛内的发电机和负荷节点分配如表1所示。

图3为解列后形成的2个电力孤岛内发电机的频率，可以看出孤岛I内的有功功率不足，发电机组频率下降较快，需要采取切负荷措施保证孤岛的稳定；在电力孤岛II内的发电机组频率增大，需要采取切机措施维持孤岛的稳定。

对于解列断面8—9，4—3，14—15(前面的节点表示在电力孤岛I内，后面的节点表示在电力孤岛II内)，利用双向潮流跟踪算法得到在各孤岛内需要控制的发电机或负荷节点。

图2 孤岛内的实时校正控制流程Fig.2 Flow chart of real-time correction control in island

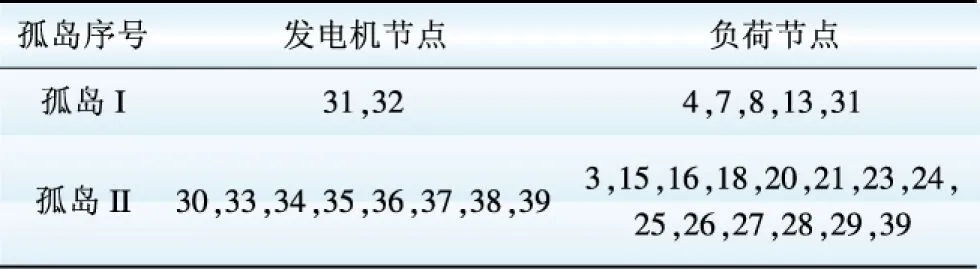
图3 解列后各电力孤岛内发电机的频率Fig.3 Frequency of generators in each island after separation

在孤岛I内，利用顺向的潮流跟踪算法进行潮流跟踪直到全部的负荷节点，可以得到需要控制的负荷节点为节点4和8；在孤岛II内，利用逆向的潮流跟踪算法进行潮流跟踪直到全部的发电机节点，可以得到需要控制的发电机节点为节点30，33，35，37和39。

利用直流潮流算法和PQ分解潮流算法对控制后的各电力孤岛进行潮流计算。首先对控制量进行直流潮流计算，确定切机切负荷控制量，如果不满足线路的功率传输要求，调整切机切负荷控制量。孤岛的控制对象和控制量，如表2所示。

表2 电力孤岛切机切负荷的控制对象和控制量
Table 2 Controlled object and quantity with generator tripping and load shedding in island

利用解列断面组成的支路集对形成的各个孤岛中每台发电机和负荷进行有功功率灵敏度分析，并结合控制对象与解列断面的电气距离和实际有功功率，确定控制次序。在电力孤岛I中，解列断面的支路集对负荷节点4的灵敏度稍大于对负荷节点8的，所以先对负荷节点4进行控制，接着对负荷节点8进行控制。利用仿真软件模拟切负荷操作，可以得到在孤岛系统I内的2台发电机的转速和频率，如图4所示。

经过切负荷控制后，发电机的频率较控制前有了很大的改善，能够维持在60 Hz附近，且发电机转速也达到稳定值，所以孤岛I达到稳定运行状态。在对孤岛系统实施控制后，得到稳定运行后的线路功率和节点电压。

对于电力孤岛II，对需要控制的发电机进行切机，通过分析解列断面支路对发电机的灵敏度，得到孤岛内支路对控制发电机的灵敏度，如表3所示。

根据解列支路对发电机的灵敏度依次进行切机，得到控制后电力孤岛的稳定运行结果。图5为孤岛II内发电机的转速和频率。孤岛II经过切机控制后，发电机的频率较控制前减小，并得到很大的改善，能够维持在60 Hz附近，且发电机转速也达到稳定值，所以孤岛II达到稳定运行状态。

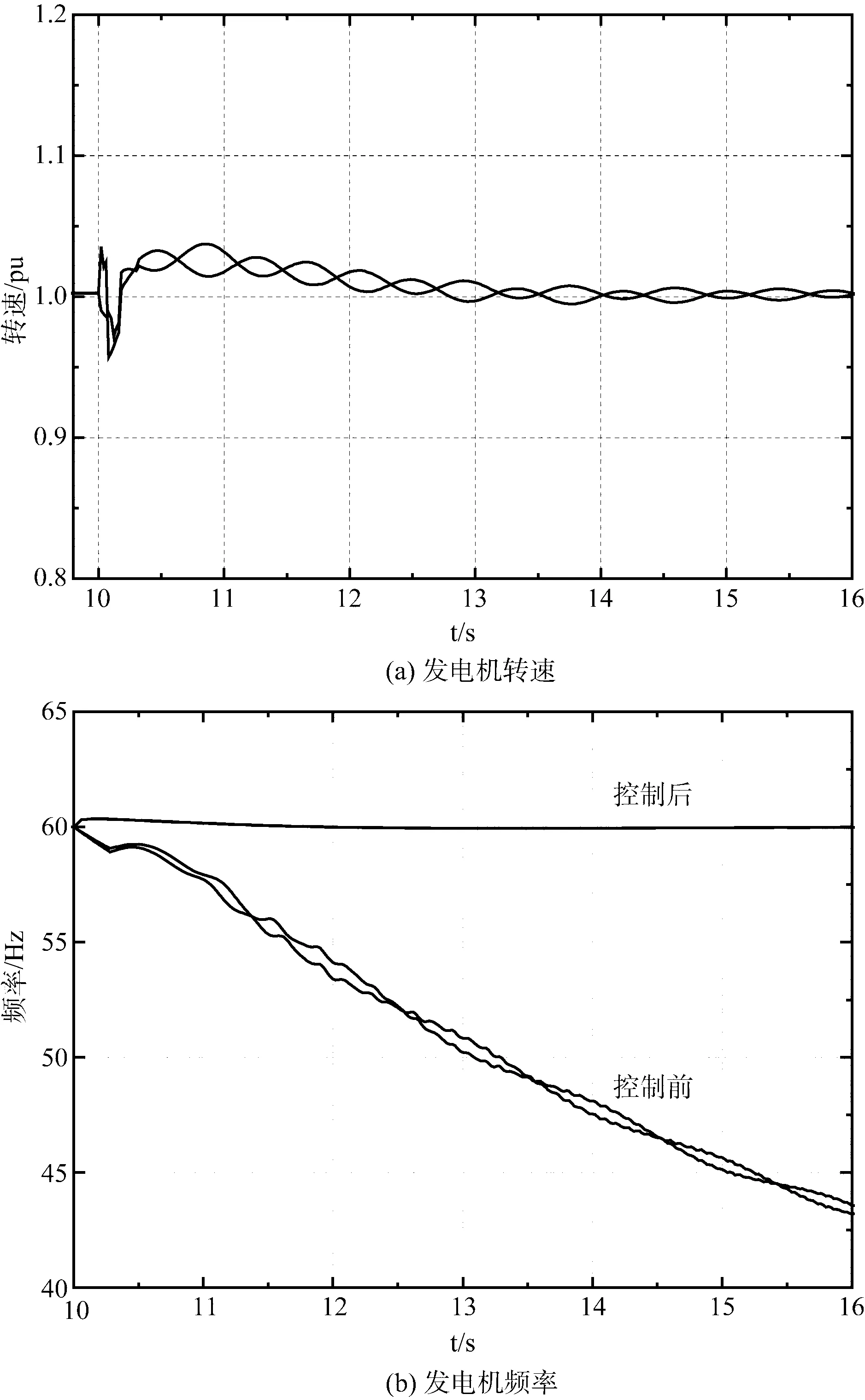
图4 电力孤岛I控制后的发电机转速和频率Fig.4 Generator rotate speed and frequency adjusted in island I

4 结 论

本文基于双向潮流跟踪算法和直流潮流算法，提出了一种电力孤岛内实时校正控制策略的快速求取方法。本方法主要是实现解列后各电力孤岛内的功率平衡和稳定运行，提高了孤岛内校正控制策略的求取速度和精度，保证了主动解列控制的稳定性。

孤岛内校正控制既能够保证解列后孤岛内的功率平衡和发电机组的同步运行，也有利于后续的自愈恢复控制。新英格兰39节点系统仿真算例结果表明，对解列后的电力孤岛实施校正控制后，能够保证孤岛系统内的发电机同步稳定运行和频率稳定，具有较好的控制效果。

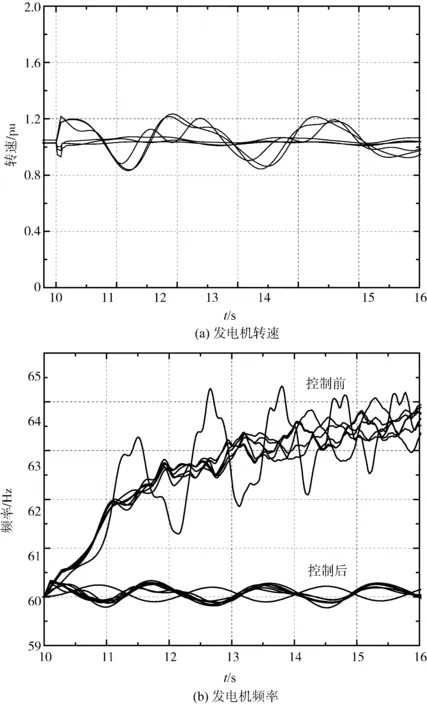
图5 电力孤岛II内控制后的发电机转速和频率Fig.5 Generator rotate speed and frequency adjusted in island II

[1]汤涌. 基于响应的电力系统广域安全稳定控制[J]. 中国电机工程学报,2014,34(21):5041-5050. TANG Yong. Response-based wide area control for power system security and stability[J]. Proceedings of the CSEE，2014,34(21):5041-5050.

[2]汤涌, 顾卓远. 区域电网远端故障引发互联系统稳定破坏现象探究[J]. 电网技术,2014, 38(1):154-159. TANG Yong, GU Zhuoyuan. A study on effect of fault occurred in remote end of regional power grid on transient of interconnected power system[J]. Power System Technology,2014,38(1):154-159.

[3]印永华, 郭剑波, 赵建军, 等. 美加“8.14”大停电事故初步分析以及应吸取的教训[J]. 电网技术, 2003, 27(10): 8-11. YIN Yonghua，GUO Jianbo，ZHAO Jianjun，et al. Preliminary analysis of large scale blackout interconnected North America power grid on August 14 and lessons to be drawn [J]. Power System Technology, 2003, 27(10): 8-11.

[4]ANDERSSON G，DONALEK P，FARMER R, et al. Causes of the 2003 major grid blackouts in North America and Europe, and recommended means to improve system dynamic performance[J]. IEEE Transactions on Power Systems, 2007, 22(3): 1012-1018.

[5]汤涌, 卜广全, 易俊. 印度“7.30”、“7.31”大停电事故分析及启示[J]. 中国电机工程学报, 2012, 32(25): 1-7. TANG Yong，BU Guangquan，YI Jun.Analysis and lessons of the blackout in Indian power grid on July 30 and 31, 2012[J]. Proceedings of the CSEE, 2012, 32(25): 1-7.

[6]汤涌. 电力系统安全稳定综合防御体系框架[J]. 电网技术, 2012, 36(8): 1-5. TANG Yong. Framework of comprehensive defense architecture for power system security and stability[J]. Power System Technology, 2012, 36(8): 1-5.

[7]PROASETIJO D, LACHS W R, SUTANTO D. A new load shedding scheme for limiting underfrequency [J]. IEEE Transactions on Power Systems, 1994, 9(3):1371-1381.

[8]高林, 戴义平, 马庆中, 等. 特高压线路解列后区域互联电网一次调频稳定性研究[J]. 电网技术, 2009, 33(20): 27-32. GAO Lin, DAI Yiping, MA Qingzhong, et al. Research on stability of primary frequency regulation of interconnected power system after trip-out Ultra High Voltage transmission line[J]. Power System Technology, 2009, 33(20): 27-32.

[9]张志强, 徐友平, 袁荣湘, 等. 大型互联区域电网解列后送端电网频率特性及高频切机方案[J].电网技术, 2015,39(1):287-293. ZHANG Zhiqiang, XU Youping, YUAN Rongxiang, et al. Frequency characteristics of power grid at sending end of split large-scale interconnected regional power grid and corresponding over-frequency generator-tripping scheme[J]. Power System Technology, 2015, 39(1): 287-293.

[10]俞璐, 武群丽, 杨雨昂, 等. 快速解列判据在多通道互联电网中的应用研究[J]. 电力建设, 2014, 35(4): 38-43. YU Lu, WU Qunli, YANG Yuang, et al. Application research of fast splitting criterion in multi-channel interconnected power system[J]. Electric Power Construction, 2014, 35(4): 38-43.

[11]DELFINO B, MASSUCCO S, MORINI A, et al. Implementation and comparison of different under frequency load-shedding schemes [C]//IEEE PES Summer Meeting, Vancouver, Canada, 2001, 1:307-312.

[12]熊小伏, 周永忠, 周家启. 计及负荷频率特性的低频减载方案研究[J]. 中国电机工程学报, 2005, 25(19): 48-51. XIONG Xiaofu, ZHOU Yongzhong, ZHOU Jiaqi. Study of under frequency load shedding scheme based on load frequency characteristics[J]. Proceedings of the CSEE, 2005, 25(19): 48-51.

[13]张瑞琪, 闵勇, 侯凯元. 电力系统切机/切负荷紧急控制方案的研究[J]. 电力系统自动化, 2003,27(18):6-12. ZHANG Ruiqi, MIN Yong, HOU Kaiyuan. A new method for generation shedding and load shedding in power system emergercy control[J]. Automation of Electric Power Systems, 2003,27(18):6-12.

[14]倪向萍, 张雪敏, 梅生伟. 基于复杂网络理论的切机控制策略[J]. 电网技术, 2010, 34(9): 35-41. NI Xiangping, ZHANG Xuemin, MEI Shengwei. Generator tripping strategy based on complex network theory[J]. Power System Technology，2010, 34(9): 35-41.

[15]王彪, 方万良, 罗煦之. 紧急控制下最优切机切负荷方案的快速算法[J]. 电网技术, 2011, 35(6):82-87. WANG Biao, FANG Wangliang, LUO Xuzhi. A fast algorithm of optimal generator and load-shedding for emergency control[J]. Power System Technology，2011, 35(6):82-87.

[16]APONTE E E，NELSON J K.Time optimal load shedding for distributed power systems[J].IEEE Transactions on Power Systems，2006，21(1)：69-277.

[17]吴晓蓉, 谢开贵, 周家启. 基于电流分解的输电损耗分摊双向追踪方法[J]. 中国电机工程学报, 2005, 25(21): 24-29. WU Xiaorong, XIE Kaigui, ZHOU Jiaqi. Transmissiong loss allocation method based on current decomposition and bi-directional trace[J]. Proceedings of the CSEE, 2005, 25(21): 24-29.

[18]赵渊, 周家启, 周念成, 等. 发输电系统可靠性评估的启发式就近负荷削减模型[J]. 电网技术, 2005,29(23):34-39. ZHAO Yuan, ZHOU Jiaqi, ZHOU Niancheng, et al. A heuristic approach to local shedding scheme for reliability assessment of composite generation and transmission system[J]. Power System Technology，2005,29(23):34-39.

[19]贾宏杰, 穆云飞, 余晓丹. 基于直流潮流灵敏度的断面潮流定向控制[J]. 电力系统自动化, 2010, 34(2): 34-38. JIA Hongjie, MU Yunfei, XU Xiaodan. Directional control method to interface power based on DC power flow and sensitivity[J]. Automation of Electric Power Systems, 2010, 34(2): 34-38.

[20]宋洪磊, 吴俊勇, 郝亮亮. 考虑同调约束的电力系统主动解列断面的搜索方法[J]. 电力系统自动化, 2014, 38(14):49-54. SONG Honglei, WU Junyong, HAO Liangliang. A searching method for power system controlled islanding surfaces considering coherency constraint[J]. Automation of Electric Power Systems, 2014, 38(14):49-54.

(编辑 张小飞)

Correction Control Strategy of Islanded Power Grid after Separation

SONG Honglei1, LI Xiaofei2, WU Junyong3,HU Jialin4, WANG Zhenming1

(1.State Grid Corporation of China AC Construction Branch, Beijing 100052, China;2. NARI Group Corporation State Grid Electric Power Research Institute, Nanjing 21106, China;3. School of Electrical Engineering, Beijing Jiao Tong University, Beijing 100044, China;4. School of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206, China)

After the implementation of controlled islanding on unstable system, the separation surfaces split the whole system into two or more power islands. It is necessary that effective correction control measures are adopted to ensure the stable operation of each island. This paper proposes rapid real-time correction control strategy based on the bidirectional power flow tracing algorithm and DC flow algorithm of separation surface. Through the power flow tracing algorithm of separation surfaces, we obtain the adjustment object (generator and load) and quantity of island, and check the result with using DC flow algorithm to maintain transient stability under the condition that the islands satisfy the security and stability constraints. Simulations on the New England 39-bus system validate the effectiveness and flexibility of the proposed approach.

separation island; correction control; power flow tracing algorithm; DC flow algorithm; load shedding and generator tripping

TM 712

A

1000-7229(2016)04-0124-07

10.3969/j.issn.1000-7229.2016.04.019

2015-11-06

宋洪磊(1985)，男，博士，研究方向为电力系统稳定与控制、电力建设等；

李晓飞(1993)，女，硕士研究生，研究方向为电力系统稳定与控制；

吴俊勇(1966)，男，博士，教授，博士生导师，主要研究方向为电力系统分析与控制，新能源发电和智能电网。