基于Gardner环的码元同步技术研究

2016-02-23施雪薛团结

微型电脑应用 2016年10期

施雪，薛团结

基于Gardner环的码元同步技术研究

施雪，薛团结

针对全数字接收机中码元同步问题,采用Gardner环实现时钟同步。其中插值和Gardner算法是关键技术，详细介绍了插值滤波器的原理和Gardner算法的来源。Gardner算法是独立于载波相位的，每个符号只要两个样值就可以进行定时误差估计，而插值器是基于多项式的滤波器，由信号采样值计算出在最佳抽样时刻的近似值，最后通过仿真表明线性插值器就能得到很好的效果，定时误差的值可以发现定时是否准确。进而通过控制器调整重采样时间，进行新的插值，获得同步。

全数字接收机；码元同步；Gardner环；插值

0 引言

码元同步是全数字解调过程中的关键步骤，它的作用是将经过匹配滤波之后的数据按照符号速率在最佳采样点获得数据的值。如果码元同步错误或者不准确，将会影响信号接收的准确性。在传统的接收机中，可以通过迟早门判断出码元信息超前或滞后的程度，将误差信息经过锁相环反馈给压控振荡器，从而调整码元位置，实现码元同步，进而获取最佳采样点。但是这个方法在全数字接收机中是不能使用的，因为接收机中的A/D采样时钟是固定的，并且接收机的采样时钟与发送码元速率独立，那么就不能保证最佳采样点能够被采样到。全数字接收机与传统的无线电数字通信接收机的主要区别，在于数字通信接收机的模拟处理区引入了数字处理技术。基本的全数字接收机是在接收机的解调器前插入A/D变换器，把接收下变频后的模拟信号变为数字信号如图1所示：

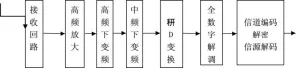
图1 基本的无线电全数字接收

由于接收机的采样速率和发送的符号速率是相互独立的，最佳采样点的值不能通过直接采样得到，需要在非同步的采样数据之间进行插值，来获得同步的信号样值。在全数字接收机中，通过定时误差估值控制的内插滤波器对得到的样本值进行插值运算，从而得到信号在最佳采样时刻的近似值。全数字接收机的定时恢复反馈式结构如图2所示：

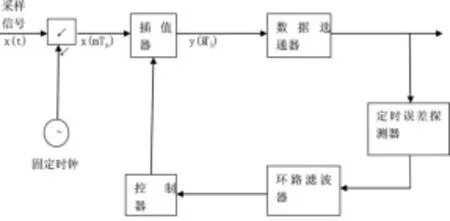
图2 定时恢复环路

信号样值x(mTs)是以固定的采样间隔Ts得到的，插值器用这些信号样值计算出插值，且在间隔Ti重样得y(kTi)，数据选通器通过这些样值计算出选通值。这个反馈环中的所有元素都是为同步做准备的，探测器检测到误差信号，误差信号经过环路滤波器，滤波器的输出驱动控制器，本文主要研究插值器和误差探测器。

1 环路结构

在数字通信中，信息是由连续的码元传递的。这些码元具有相同的持续时间。接收端接收这个码元序列时，一般需要知道每个码元的起止时刻，从而对码元进行判决。用判决器对信号进行判决时，需要找到每个码元最大值的采样点位置。所以接收端必须要产生一个定时脉冲序列，且频率和相位要与接收码元一致来保证采样判决时刻与信号码元的最大值的位置保持一致，即最佳采样点问题。采用一般的调整采样时钟的方式无法消除这个问题，必须用内插的方法来对时钟相位进行调整，从而找到最佳采样点。

Ganrder算法是一种不需要先进行载波同步的定时误差估计算法。这种方法是一种非判决指向方法，其基本思想是：提取出相邻码元最佳采样点的幅度和极性变化信息，再加上相邻码元过渡点是否为零这一信息，就可以从采样信号中提取出定时误差。

在系统设计中Gardner环位于Costas载波同步锁相环之后，主要由4部分组成：内插器，误差探测器，环路滤波器和控制器模块。Gardner算法基本结构[3]以QPSK调制信号为例，如图3所示：

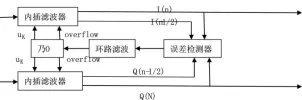
图3 Gardner环结构框图

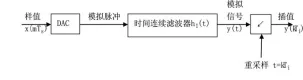
图4 速率转换模型

I.Q两路信号的采样点通过运算后，其每个符号将会产生一个定时错误样点，通过误差检测模块将定时错误序列通过环路滤波器后送给NCO，这里的NCO是递减模块，由NCO产生参数控制插值滤波器，使其进行重采样时刻调整，从而达到信号的最佳采样点的位置，完成整个符号的同步过程。

1.1 插值方程

如图4所示：

图4是一个虚拟的，模拟/数字混合速率转换模型[2]，把样值转换成加权模拟脉冲序列，这些序列经过连续的模拟插值滤波器，滤波器的脉冲响应为ℎI(t)。滤波器的输出为式（1）：

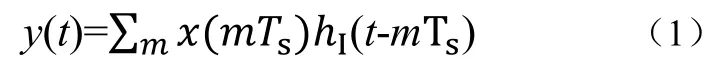
由观察可知y(t)≠x(t)，和大多数传统的插值器相反，在这里没必要恢复最初的信号x(t)波形。

现在以采样间隔t=kTi重新采样y(t),Ti与信号码元是同步的。正常情况下TiTs⁄是无理数，采样和符号速率是不行等的。新的样值（插值）为式（2）：

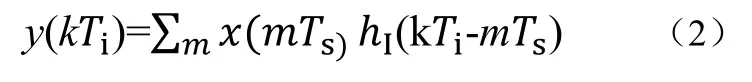
尽管这个模型包括一个虚拟的DAC和模拟滤波器，但是式（2）中的插值可以完全数字化实现只要有以下3个条件：

（1）输入序列{x(m)}，（2）插值滤波器的脉冲响应hI(t)，（3）输入和输出样值的时间间隔mTs和kTi。这些数字化计算出的插值和模拟方法算出的值本质是相同的。通过对式（2）重新设置，可以得到一个更有效的公式。重新设置m为信号索引，定义一个滤波器索引为式（3）：

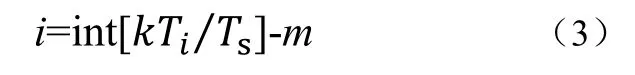
其中int[z]表示不超过z的最大整数。同样的定义一个基本指针mk和一个分数间隔uk为式（4）、（5）：

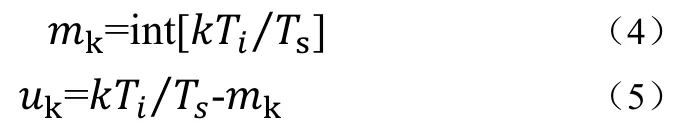
(0≤uk＜1) 定时关系如图5所示：

输入采样时间

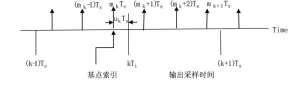
图5 采样时间关系

由公式（4）和（5）得m=mκ-i和(kTi-mTs)=(i+uk)Ts，且插值是在时刻kTi=(mk+uκ)Ts计算得到的。

等式（2）可重新写为：y(kTi)=y[(mk+uk)Ts为式（6）：

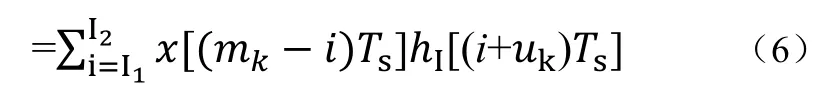
式（6）是数字插值的基本方程。

1.2 插值滤波器

滤波器是实现插值的基础，但插值滤波器在设计时,无须像常规滤波器设计那样要体现滤波器的系数，插值滤波器的目的是插值运算输出，无需真实的构建滤波器。在选择插值滤波器系数时，需要注意以下两点：（1）基本采样点数及参与运算的样点数应当是偶数；（2）要插值的点应当在基本采样点中间。其中前者是让滤波器具有线性相位，后者的约束是为了避免插值中的延时干扰。

可以作为插值滤波器的函数有无穷多种，其中一类是基于多相式的滤波器，即滤波器的脉冲响应是关于t的一个多项式，或者是关于t的一个分段多相式。一个N点{ti，x(i)}的经典多相式插值可以通过拉格朗日插值表示，即为式（7）：

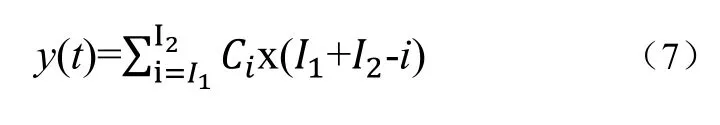
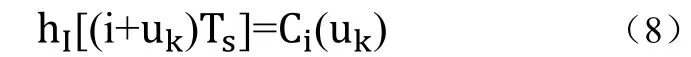
整个插值过程可以由图6清晰看出。图中表示的是信号的频谱图，由频谱图可以明显的看出x(t)≠y(t)。

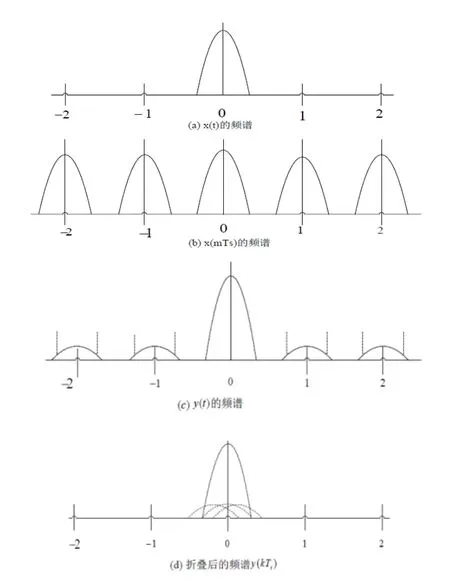
图6 信号频谱

图6（a）是输入信号x(t)的频谱图。图6（b）是抽样信号x(mTs)的频谱图，没出现频谱混叠。

图6（c）展示了插值滤波器不理想时，信号y(t)的频谱，其中残留的镜像频谱清晰可见。以1/Ti的速率重采样后，残留的镜像频谱将于有用信号频谱混叠。理性的插值滤波器能完全的抑制所有的1/2Ts以外的频谱成份,因此任何实际的滤波器由于不完全的阻带衰减会带来信号失真。

在实际的调制解调器中，简单的插值就会得到很好的结果，在大多数情况下两点的线性插值就足够了，因此本文使用线性插值滤波器。线性插值滤波器的系数为式（9）：

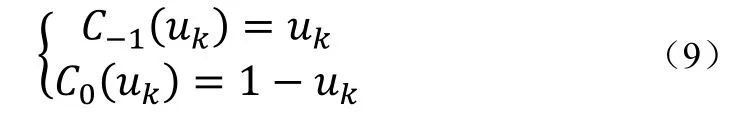
线性插值可由式（10）实现式（10）：

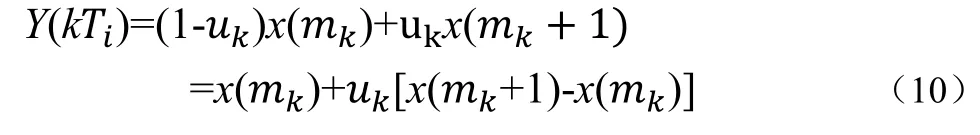
2 Gardner定时误差模型

随着在接收端用采样来形成数字信号的普遍，数字信号处理器的性能也得到了提高，同时带来了需要用与采样点有关的算法来取代长期以来占据主导地位的连续时间方法的要求。一个经典的I-Q接收调制解调器模型如图7所示：

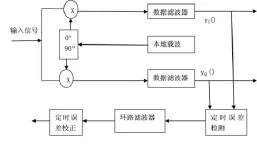
图7 接收模型

数据滤波器在相乘器后面，通过滤波形成信号脉冲，降低噪声，抑制多余的乘积项。我们并不详述采样点，仅是说明滤波器的数出只能是形如{yI()｝和{yQ()}的一对实序列，定时信息需要从这些序列中检测出来。符号以间隔T同步的传输，每个序列中包含有符号的两个样值，并且序列中的样值在时间上是一致的。两个样值中，一个是在选通点处得到，另一个是在两个选通点的中间处得到的。

用r来表示符号数，那么第r的符号的选通值可以表示为yI(r)和yQ(r),为了形式上的统一，把位于第(r-1)个和r个选通值之间的样值表示为和。定时误差探测器是对样值进行计算，对每个符号产生产生一个误差样值ut(r)。误差探测器[3]的算法为式（1）：

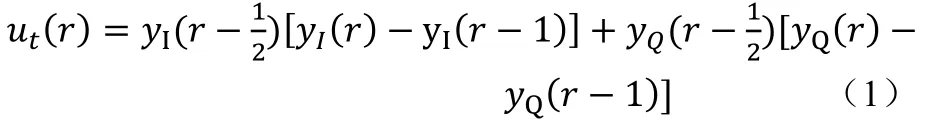
误差信号有正值也有负值。假如定时超前，无论第r和r-1个样点的符号是相同还是相反，ut(r)＜0,如果定时滞后，ut(r)＞0。若定时准确，yI(r)和yI(r-1)将对应最大采样值则正好采样到零点，正交分量yQ(r)也将如此。此时定时误差ut(r)等于零。yI(r)和yI(r-1)异号或者yQ(r)和yQ(r-1)异号，才能使用式(11)计算定时误差。这些同步关系可以用图8所示：

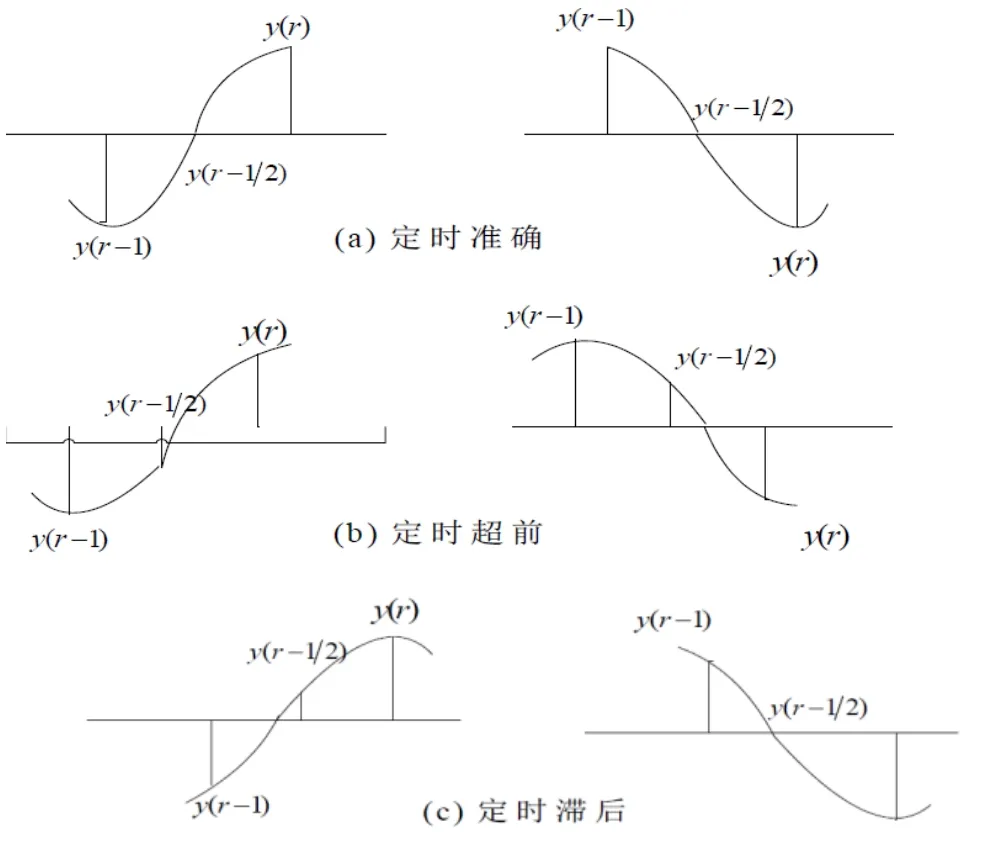
图8 同步关系图

如在图8(a)中所示，当定时准确时，ut(r)=0;当定时超前时，如图8(b)中所示，ut(r)＜0;当定时滞后时，如图8(c)中所示，ut(r)＞0。

ut(r)与载波相位相互独立，不需要在锁定定时相位之前，先锁定载波相位。Gardner算法可以用于在信号的额外带宽约为信号带宽的40%～100%，这一信号范围是以卫星通信为代表的。在更窄的带宽下，会使噪声性能变差。

Research on Symbol Synchronization Technology Based on Gardner Loop

Shi Xue, Xue Tuanjie
(Hohai University, Nanjing 211100, China)

Aiming at the problem of symbol synchronization in all-digital receiver, this paper employs the Gardner loop to realize timing synchronization. The interpolation and Gardner algorithm are the key technology. The paper introduces the theory of interpolation filter and origin of Gardner algorithm. The arithmetic is independent of carrier phase, and requires only two samples per symbol for timing-error estimation. The interpolator is a filter which is based on polynomials, and it figures out the approximation from samples in optimum time and comes true by simulation. The simulation indicates that linear interpolation gives excellent performance, and the value of timing-error can discover accuracy of timing. What’s more, it uses the value to adjust the resample time by controller. Then the interpolator will have a new interpolation to contribute to synchronization.

All-digital receiver; Symbol synchronization; Gardner loop; Interpolation