微电网中分布式发电的荷电状态控制策略

张晨晨, 张鸿鹄, 胡超

(1.国网安徽省电力公司检修公司,安徽 合肥 230000; 2.合肥工业大学,安徽 合肥 230009)

微电网中分布式发电的荷电状态控制策略

张晨晨1, 张鸿鹄1, 胡超2

(1.国网安徽省电力公司检修公司,安徽 合肥 230000; 2.合肥工业大学,安徽 合肥 230009)

微电网中分布式发电(DG)需要搭配储能模块满足持续的供电需求，如何对储能模块的SOC进行控制就非常重要。在传统下垂控制的基础上，增加了基于比例积分(PI)调节器的荷电状态(SOC)控制环节，并在建立小信号模型的基础上，通过极点配置的方式设计了调节器参数，使得系统具有良好的动态性能，最后通过仿真验证了控制策略的正确性和可行性。

微电网；储能；分布式发电；荷电状态；极点配置

0 引 言

随着能源和环境问题越来越突出，基于光伏、风能等各种清洁能源的分布式发电DG得到了广泛的发展，然而传统的DG大多具有间歇性，不稳定性等特点，随着电网渗透率的不断提升，给电网的稳定运行带来一系列问题。近年来一种由分布式电源、储能系统、负荷和保护装置汇集而成的微电网[1-3]已经成为DG与电网连接的有效模式。通过增加储能装置，使得微电网不再是传统DG的单向功率源，而是具有了能量缓冲的能力。通过设计合适的控制策略，微电网可以作为电力系统中的具有独立运行能力的子模块，孤岛状态下，微电网可以作为电源为内部负荷供电，并网状态下，微电网又可以参与电力系统调度，增加电力系统运行的可靠性。

微电网中的DG作为可控电源，需要搭配储能单元ESU，常用的是铅酸或锂电的蓄电池组[4-5]。DG单元通常采用下垂控制算法，其基本思想是，逆变器检测自身输出功率，作为反馈量调整输出电压和频率指令，并通过闭环控制对指令进行跟随[6-7]。通过下垂控制，孤岛运行时DG能够均分负荷，而在并网运行时则具备传统DG电流源的特点，能够与电网之间交换指令功率，具有更大的自由度，因此本文也采用下垂控制作为DG的控制策略。

微电网中的DG作为可控电源，需要搭配储能单元ESU，针对ESU的SOC进行控制，提高微电网的运行效率及与大电网之间相互协调作用，是微网研究的热点[8-9]。当DG处于孤岛模式时，此时DG始终处于放电模式，SOC控制的目的通常在于使各单元SOC更加快速稳定的趋于统一，以提高整个微网带负荷运行的时间[10]，而在并网状态下，DG需要具备调峰填谷的效果，当电力系统负荷较低时，DG吸收电网功率，反之电力系统负荷较大时释放功率，该功能主要由微网的能量管理系统EMS进行调度，即EMS向各台DG发送SOC指令值，DG接到指令信号后调整自身运行工况使自身SOC跟踪指令要求。

本文针对并网状态下DG的SOC控制方法进行了深入研究。首先分析了DG中储能单元，下垂控制算法及逆变器闭环控制的数学模型，并通过小信号分析给出了采用比例积分调节器的SOC控制的参数选择，能够有效的使得系统对SOC指令实现无静差跟随。最后通过仿真验证了本文提出的控制策略的良好性能。

1 系统数学模型

本文提出的微电网具有如下结构，如图1所示。每个DG单元均包含储能单元，三相变流器以及LC滤波器，下垂控制算法通过检测输出功率，并生成指令电压。储能单元需要根据运行工况及电网状态动态改变自身SOC，提高电力系统频率的稳定性。

图1 DG单元结构

1.1 储能单元模型

图2 储能单元模型

蓄电池具有复杂结构的电化学单元，其等效电路模型也居于多种形式。为简化控制算法，易于扩展，本文采用Rint模型作为单个电池单元形式，其基本电路为戴维南电路等效结构，为受控电压源与输出阻抗的串联形式，电池组数学模型则可用单个模型电池等效串并联获得，如图2所示。

电池模型中输出阻抗为纯阻性电阻Rbat，ibat为电池输出电流，受控电压源电压Ebat与电池SOC之间存在非线性关系，如图3所示。

图3 Ebat与SOC关系曲线

根据文献[11]给出的控制算法，通过数学模型对图3中的关系进行曲线模拟，有：

(1)

其中E0为电池空载电压，K、A、B为电池模拟参数，需要通过实验测试获得，SOC采用下式进行估计，为:

(2)

其中SOC0为初始荷电状态，Qbat为电池容量，ibat为输出电流。

1.2 下垂控制

下垂控制中，逆变器输出电压、频率与检测功率之间存在如下关系：

ω=ω0+m(Pref-P)

(3)

U=U0+n(Qref-Q)

(4)

其中Pref、Qref分别为同步电机的有功给定，P、Q分别为DG的检测有功和无功输出，ω0U0分别为空载频率和空载电压，m、n分别为有功和无功下垂系数。P、Q根据DG的实际输出Po、Qo经过一阶低通滤波器获得，有:

(5)

其中T为低通滤波器的惯性时间常数，若电网电压和频率与逆变器空载电压和频率相同，则可得到DG稳态下输出功率为P=Pref，Q=Qref。因此，并网状态下DG可以认为是一个可控功率源。本文将SOC作为控制量引入下垂算法，采用基于比例积分调节器的SOC控制模块，其控制方程如下：

Pref=kp(SOCref-SOC)+ki∫(SOCref-SOC)

(6)

其中SOCref为SOC指令值，kp和ki分别为SOC控制的比例系数和积分系数。综合式(3)(4)(5)(6)，并考虑到θ= ∫ω，即可得到逆变器的电压指令U∠θ。图4给出了基于上述思想的DG并网控制策略。

图4 DG控制策略

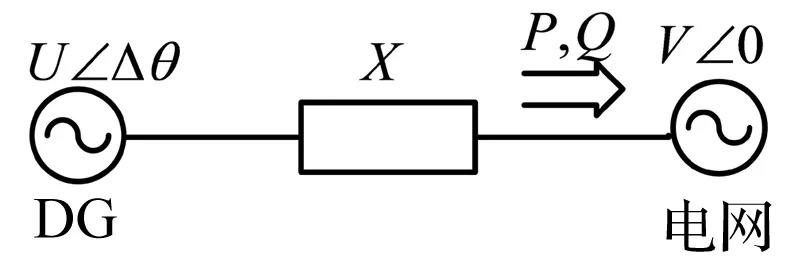
图5 DG等效模型

在获得指令电压后，通过电压双闭环控制以及SVPWM调制，使得输出电压跟随指令值。由于电压控制部分响应速度远大于功率控制部分，因此DG输出端可视为U∠θ的三相恒压源。其并网状态下的等效模型如图5所示。

其中U为DG端口线电压有效值，V为电网线电压有效值，Δθ为DG与电网间相角差，X为线路阻抗并近似为纯感性，从而得到DG输出功率与相角差之间的近似关系为:

(7)

2 基于PI调节器的SOC控制策略分析

通过上述分析得到整个DG系统的数学结构模型，可以建立系统的SOC控制框图，如图6所示，由于SOC仅取决于P的变化，可忽略无功控制过程，将U认为是恒定值。

图6 SOC控制框图

可以得到系统闭环特征方程如下:

Ts4+s3+mA(1+Tkp)s2+

mAB(Tki+kp)s+kimAB=0

(8)

图7 系统根轨迹图

图8 指定参数下SOC指令的单位阶跃响应

对于高阶系统，其动态性能及稳定性主要取决于主导极点，通过选择合适的参数将主导极点配置为s1,2=-1±j，阻尼比为0.707；将非主导极点配置为s3,4=-30±j40，阻尼比0.8。图8所示为该参数下SOC指令的单位阶跃响应。

3 仿真分析

为了验证算法有效性，根据图1搭建单机DG并网的仿真平台，具体参数如表1所示。

表1 基于储能变流器的DG参数

初始状态下SOC为50%，0.1秒时SOC指令阶跃10%，图9(a)(b)分别为某一具体参数下，SOC调节器及T,m变化下系统的响应波形，从上到下依次为SOC，输出功率P以及DG频率ω。通过比较发现，kp、ki主要影响SOC控制效果，T、m则主要影响DG输出功率P和输出频率ω。总的来说，较大的kp、ki有利于提高系统响应速度，降低SOC调节时间，但DG越容易出现过载，ω越偏离额定频率ω0。T、m对SOC控制的效果基本没有影响，但T越大、m越大DG输出功率越容易发生震荡，这主要是由于非主导极点偏离实轴导致。

图9 不同参数下SOC指令阶跃时DG波形

4 结束语

本文针对微网中DG的SOC控制问题，提出了一种基于PI调节器的控制算法。通过分析下垂控制和SOC控制算法得到系统的小信号模型，并从极点配置的角度设计了调节器的参数，使得系统能够同时具备稳定性和良好的动态性能，最后通过仿真和实验验证了本文提出算法的有效性。

[1] 曾正，赵荣祥，汤胜清，等．可再生能源分散接入用先进并网逆变器研究综述[J]．中国电机工程学报，2013， 33(24)： 1-12．

[2] JOSEP M GUERRERO, LUIS GARCA DE VICUA, JOSÉ MATAS, et al. A wireless controller to enhance dynamic performance of parallel inverters in distributed generation systems[J]. IEEE Transactions on Power Electronics, 2004, 19(5): 1205-1213.

[3] JOSEP M GUERRERO, LUIS GARCA DE VICUA, JOSÉ MATAS, et al. Wireless-control strategy for parallel operation of distributed-generation inverters[J]. IEEE Transactions on Industrial Electronics, 2006, 53(5): 1461-1470.

[4] 荆龙，黄杏， 吴学智，改进型微源下垂控制策略研究[J]，2014,29(2)：145-152.

[5] 龙江涛,路嘉鑫,钱希森. UPS逆变器并联控制技术综述[J]. 电源学报, 2013,12(5): 21-27.

[6] 陈树勇, 鲍海, 吴春洋. 分布式光伏发电并网功率直接控制方法[J]. 中国电机工程学报, 2011, 31(10): 6-11.

[7] 陈昌松, 段善旭, 殷进军. 基于发电预测的分布式发电能量管理系统[J]. 电工技术学报, 2010, 25(3): 150-156.

[8] 谢玲玲, 时斌. 基于改进下垂控制的分布式电源并联运行技术[J]. 电网技术, 2013,57(3): 992-998.

[9] 于玮, 徐德鸿. 基于虚拟阻抗的不间断电源并联系统均流控制[J]. 中国电机工程学报, 2009, 29(24): 32-39.

[10] XIAONAN LU. State-of-charge balance using adaptive droop control for distributed energy storage systems in DC microgrid applications[J].IEEE Transactions on Industrial Electronics, 2014, 61(6): 2804-2815.

[11] O TREMBLAY，LA DESSAINT，AI DEKKICHE.A generic battery model for the dynamic simulation of hybrid electric vehicles[C].IEEE Vehicle Power & Propulsion Conference, 2007:284-289.

Control Strategy of Charge State of Distributed Generation in the Micro Grid

Zhang Chenchen1, Zhang Honggu1, Hu Chao2

(1. State Grid Anhui Provincial Electric Power Company, Hefei Anhui 230000 China；2. Hefei University of Technology, Hefei Anhui 230009,China)

Distributed generation (DG) in micro grid needs to provide the energy storage module to meet the demand for continuing power supply, how to control SOC in the energy storage module is very important. To solve this issue, on the basis of the traditional droop control, a control unit for state of charge (SOC) based on proportional integral (PI) regulator is added. On the basis of the establishment of small-signal model, the regulator parameters are designed via pole assignment to enable the system presenting sound dynamic performance. Finally, the simulation shows the correctness and feasibility of the control strategy.

micro grid；energy storage；distributed generation；state of charge；pole assignment

10.3969/j.issn.1000-3886.2016.05.015

TM91

A

1000-3886(2016)05-0044-03

张晨晨(1988-),男，安徽安庆人，大学，技师，电气工程及其自动化。 张鸿鹄(1980-)男，安徽巢湖人，本科，发电厂及电力系统专业，工程师，高级技师，有多年继电保护和电气试验工作经验，现从事超高压变电站运维工作。 胡超(1985-)男，安徽巢湖人，博士生，电气工程专业。

定稿日期: 2016-04-12