基于鲁棒反演滑模控制的PMSM伺服系统控制研究

杨代利

(四川文理学院 计算机学院,四川 达州 635000)

基于鲁棒反演滑模控制的PMSM伺服系统控制研究

杨代利

(四川文理学院 计算机学院,四川 达州 635000)

为了解决永磁同步电机伺服系统PI控制对转矩干扰、参数扰动和大幅位置波动鲁棒性差等问题，将反演控制和滑模控制相结合设计了鲁棒反演滑模位置伺服控制器，通过构建虚拟控制项，利用李雅普诺夫稳定性原理推导了控制律，并进行了稳定性分析。为避免抖动现象造成高精度伺服系统无法运行，采用连续饱和函数取代继电特性的符号函数。通过与PI控制器的伺服系统仿真对比，鲁棒反演滑模控制器对不确定性、转矩干扰和自身运行导致参数摄动具有较强的鲁棒性，且响应速度快，大大削弱了抖动现象。

PI控制器；同步电机；反演控制；滑模控制；鲁棒性；抖动

0 引 言

PMSM(永磁同步电机)具有高效率、低转矩脉动、高动态性能和高能量密度等特点，在电力拖动系统和伺服控制系统中应用广泛[1]。PMSM是一个高阶、耦合性强、非线性、变参数的复杂对象，同时高性能的伺服控制系统要求具备响应快、无超调、抗干扰及调速精度高等特性。

对于模型不确定，参数摄动和不确定的外部干扰，鲁棒性是衡量控制系统响应参考输入的重要指标。传统的PID控制，控制器参数较难选取，很多工程实际多采用经验设定参数，适用于具有精确数学模型的控制系统，而对于结构模型易受到外界和自身运行情况影响的控制系统，PID控制鲁棒性较差，甚至可能达不到控制效果[2]，而鲁棒反演滑模控制具有较强的鲁棒性，结构简单，且响应较快[3]。文献[4]设计参数自适应全局滑模位置控制器克服了伺服系统不确定因素带来的影响，实现了具有一定自适应能力的高性能PMSM伺服控制系统。文献[5]中，将反演设计方法与滑模控制结合用于线性感应电机驱动控制中，增强了系统自适应性和鲁棒性。但是，滑模变结构控制在本质上的不连续开关特性,会引起系统的抖振现象，严重时，影响系统正常运行，还可能激发系统未建模部分[6]。因此，消除或削弱系统抖振已经成为滑模控制重要问题,常规滑模控制切换控制采用具有继电特性的符号函数，而符号函数是一个不连续的函数，为了更好的削弱抖振，不少文献提出连续化的饱和函数替代符号函数[7]。

本文针对PI控制器抗负载干扰、大幅位置调节和结构参数变化效果不理想，设计了一种鲁棒反演滑模控制器，该控制器综合了李雅普诺夫函数稳定性原理、反演控制和滑模控制等控制方法，在稳定性以及自适应性和鲁棒性上具有优良的特性。为了尽可能削弱颤抖，采用连续函数替代了符号函数。并将负载转矩干扰和结构参数的变化综合为一个不确定性的有界项。最后，通过仿真表明，本文所设计的鲁棒反演滑模控制器比PI控制器具有更强的鲁棒性和自适应性。

1 PMSM的数学模型

在推导PMSM的数学模型时，通常需假定：不考虑谐波以及磁路饱和、定子磁场正弦分布、忽略涡流损耗和磁滞损耗以及不考虑转子无阻尼绕组[8]。PMSM矢量控制方法是在d-q轴数学模型上进行的，它不仅可以用于分析正弦波永磁同步电动机的稳态运行性能，也可以用于分析电动机的瞬态性能。采用PMSM转子磁场定向矢量控制，通常保持d轴的电流ids=0。在d-q坐标系下PMSM状态方程：

(1)

式中uqs，iqs为定子电压、电流的q轴分量，R为定子绕组电阻，L为等效d、q轴电感，pn为极对数，ψf为转子永磁体产生的磁连，ω为转子机械角速度，J为折算到电机轴上的总转动惯量，B为粘滞摩擦，TL为折算到电机轴上的总负载转矩。

d轴电流为零，实现了PMSM的解耦。因此，电磁转矩大小与q轴电流成正比，由此可得PMSM的转矩方程：

(2)

PMSM的运动方程：

(3)

2 鲁棒反演滑模控制策略设计

2.1 PMSM的状态方程

式中θ为角位置。

则以位置和转速状态变量的状态方程为：

(4)

可得状态方程为：

(5)

考虑系统不确定性和扰动情况的状态方程：

(6)

将式(6)整理可得：

(7)

其中F为总的不确定性，

2.2 切换函数设计

首先定义李雅普诺夫函数为:

(8)

对上式进行时间求导可得：

定义虚拟控制项：

(9)

(10)

其中c1为正的常数。整理可得：

(11)

滑模PMSM位置伺服系统控制器设计包括切换函数的设计以及控制律的设计，减弱抖振的方法。切换函数的选择关系到系统状态在运动到切换面后，趋于稳定的响应速度。PMSM伺服系统状态方程在dq坐标系，是二阶系统，选择线性切换函数：

s=k1e1+e2

(12)

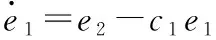
2.3 控制律设计和稳定性分析

李雅普洛夫函数是分析稳定性的重要方法，为了推导伺服系统的控制律选择李雅普洛夫函数为：

(13)

等式两边对时间求导可得：

将式(11)和式(12)代入上式得：

(14)

把式(7)和式(9)代入上式得：

(15)

根据上式，要使伺服系统最终趋于渐进稳定

可设计控制律为：

(16)

其中h和β为正的常数。

将式(15)代入式(16)得：

由于

如果保证H为正定矩阵，则有:

其中，

当参数变化大以及大范围位置控制时，伺服系统抖振可能加剧，为了削弱抖振，采用连续饱和函数取代理想滑动模态控制作用中具有开关特性的符号函数sgn(s)：

(17)

选择一个较小的正数φ，对于削弱抖振，能起到至关重要的作用。

3 仿真实验及结果

为验证所设计的鲁棒反演滑模控制器的有效性，使用MATLAB/Simulink软件电气模型库SimPowerSystems搭建仿真模型，永磁同步电机伺服系统的仿真结示意图如图1所示。

图1 永磁同步电机伺服系统鲁棒反演滑模控制系统仿真框图

PMSM参数如下：Ld=Lq=8.5 mH,Pn=4，R=2.875 Ω，J=8×10-4kg·m2，B=1×10-4N·m·s，

Ψf=0.175 Wb。

4 仿真实验

(1)当电机空载启动时，给定位置10 rad，在t=0.2 s时，位置指令变为50 rad，持续0.3 s后，给定位置回到0 rad。

图2 阶跃位置响应曲线

图3 鲁棒反演滑模控制削弱抖振 位置响应曲线

由图2可知，电机空载启动，无负载扰动和永磁同步电机固有参数没有变化时，且在给定位置大范围波动时，鲁棒反演滑模控制器响应时间较快，并在位置变化较大时，也能保持较快响应速度。从图3可得，采用饱和函数替代具有继电特性的符号函数，电机到达稳定状态其抖振大大被削弱，从而保证伺服系统能可靠的运行。鲁棒滑模反演滑模控制器，是适应同步电机位置伺服控制系统的，且响应较快。

(2)永磁同步电机带负载TL=1 N·m运行时，伺服系统给定参考位置θ=10 rad，当电机启动运行正常后，在t=0.2 s时，由于工况的变化，电机负载增加4 N·m·s，负载扰动持续时间0.1 s，然后在t=0.5 s负载转矩调整为TL=3 N·m持续运行。

图4 负载扰动对比位置响应曲线

图5 负载扰动削弱抖振位置响应曲线

从图4可得，鲁棒反演滑模控制器永磁同步电机伺服系统带负载启动后，几乎无稳定误差，而PI控制器在带载启动后，具有一定的稳态误差。且在t=0.2 s出现负载扰动时，阶跃位置响应不随负载的扰动发生波动，最后在负载转矩有所增加，其响应也基本没变化。而PI控制器易受负载扰动发生波动，位置响应出现误差，不利于高精度伺服系统的控制。由图5可知，在带载运行和负载扰动情况下，其用饱和函数使其切换符号函数连续化，能有效的削弱抖振。由此表明所设计的鲁棒反演滑模控制器对于突加的转矩干扰以及负载变化具有一定鲁棒性和自适应性。

图6 参数摄动前后鲁棒反演滑模 控制位置响应曲线

图7 参数摄动前后 PI控制位置响应曲线

(3)当同步电机伺服控制系统给定位置θ=10 rad，且带有负载TL=2 N·m，考虑电机运行时温度升高和磁路饱和等变化情况，电阻、磁链、电感参数摄动，即负载变化ΔR=0.5 Ω，电感变化ΔL=0.001 mH，磁连变化ΔΨf=0.03 Wb，仿真如图6和图7所示。

从图6和图7对比表明，永磁同步电机运行时，参数摄动引起PI控制系统出现了超调和稳态误差。而鲁棒反演滑模控制伺服系统阶跃响应稳态误差不随负载和参数摄动的影响，可见鲁棒反演滑模控制器具有较强的鲁棒性和自适应性。

5 结束语

本文为解决PI控制器存在的缺陷，将反演设计方法和滑模控制理论相结合设计了永磁同步电机伺服系统鲁棒反演滑模位置控制器。并且在永磁同步电机位置大幅波动、转矩扰动和结构参数摄动三种工作情况进行了仿真研究，仿真表明永磁同步电机鲁棒反演滑模控制器比PI控制器位置伺服系统具有更好的动态和静态性能，以及更强的抗干扰能力和鲁棒性，达到了预期的设计要求。

[1] 李珍国.交流电机控制基础[M].北京:化学工业出版社,2009.

[2] 王志,王长松.基于滑模变结构的永磁同步电机调速系统设计[J].微电机,2011，44(6):52-56．

[3] SHIEH H J,SHYU K K.Nonlinear sliding mode torque control with adaptive backstepping approach for inductionmotor drive[J].IEEE Transactions on Industrial Electronics,1999,46(2):380-389.

[4] 辛平,弭洪涛,白晶.PMSM伺服系统参数自适应全局滑模变结构位置控制器设计[J].冶金自动化,2012,36(4):69-72.

[5] F J LIN,P H SHEN,S P HSU．Adaptive Back-stepping Sliding Mode Control for Liner Induction Motor Drive[J]．IEEE Proceeding Electrical Power Application,2002,149(3):184-194．

[6] 王丰尧.滑模变结构控制[M].北京:机械工业出版社出版,1995.

[7] 刘金琨.滑模变结构控制MATLAB仿真[M].北京:清华大学出版社,2014.

[8] 王芙蓉.PMSM伺服系统滑模变结构控制研究[D].武汉:武汉理工大学,2006．

A Study on PMSM Servo System Control Based on Robust Backstepping Sliding-mode Control

Yang Daili

(College of Computer, Sichuan University of Arts and Sciences, Dazhou Sichuan 635000, China)

In order to solve such problems as interference of PI control on torque, parameter disturbance and poor robustness in the case of large positional fluctuation in the PMSM servo system, through combination of backstepping control and sliding-mode control, this paper designs a robust backstepping sliding-mode position servo controller. Through construction of virtual control, the Lyapunov stability principle is used to deduce the control law, and the stability is analyzed. The sign function of relay characteristics is replaced by the continuous saturation function to avoid that the high-precision servo system cannot operate on account of chattering. As shown in the comparison with the PI controller servo system, the robust backstepping sliding-mode controller has a strong robustness against uncertainty, torque disturbance and parameter perturbation caused by its own operation as well as high response speed, thus reducing chattering to a great extent.

PI controller;synchronous motor; backstepping control; sliding-mode control;robustness; chattering

四川文理学院面上项目资助(项目编号；2014Z002Q)

10.3969/j.issn.1000-3886.2016.05.004

TM351

A

1000-3886(2016)05-0012-03

杨代利，(1985-)，男，四川内江人，硕士生，主要研究领域为滑模控制理论、物联网。

定稿日期: 2016-06-21