WSN节能问题中基于曲线拟合的插值算法研究
2016-02-23黄兴利慕德俊焦利涛黄一杰
黄兴利,慕德俊,李 哲,3,焦利涛,黄一杰
(1.西北工业大学自动化学院,陕西西安 710072;2.温州大学商学院,浙江温州 325035;3.湖北工程学院新技术学院,湖北孝感 432000)
WSN节能问题中基于曲线拟合的插值算法研究
黄兴利1,2,慕德俊1,李哲1,3,焦利涛1,黄一杰1
(1.西北工业大学自动化学院,陕西西安710072;2.温州大学商学院,浙江温州325035;3.湖北工程学院新技术学院,湖北孝感432000)
摘要:无线传感器网络的传感器节点主要依靠电池供电,而目前节点的生存时间较短,且观测精度较低。通过对WSN能耗问题的研究,提出了基于曲线拟合的插值算法,该算法通过减少部分采样次数,使用算法将减少的数据模拟出来,最后,通过曲线拟合方法拟合出近似接近所有采样数据点的函数公式。该方法延长了节点的生存时间,间接提高了采样精度。
关键词:WSN;曲线拟合;插值算法;采样
0 引言
WSN由大量传感器节点组成,传感器节点由于受到其自身条件:分布广、分布密集,且无线传输等条件的约束,其主要依靠电池供电。目前,常见的应用于WSN网络的电池主要有镍氢电池与锂电池,电池的容量为800~3 000 mA·h,且常搭配太阳能电池板使用[1],若选用MSP430作为节点的主控制芯片,传输设备采用CC2500,在节点电源采用锂电池与太阳能电池板配套使用,且全天工作的情况下,节点电能的消耗情况如表1所示[1]。
由表1可知,节点的能量主要用于两个方面:一是节点的正常运行;二是节点的数据传输,且当节点传输频率较高时,节点的能量主要消耗在数据的传输过程中,当节点传输频率较低时,节点的能量主要消耗在维持节点正常运行上。由表1可得出,节点存在一个明显的不足之处:节点的生存时间较短,即降低节点的传输频率,节点的生存时间最长也超不过13.4 d。因此,如何提高节点的生存时间成为目前WSN网络研究人员的头等难题。
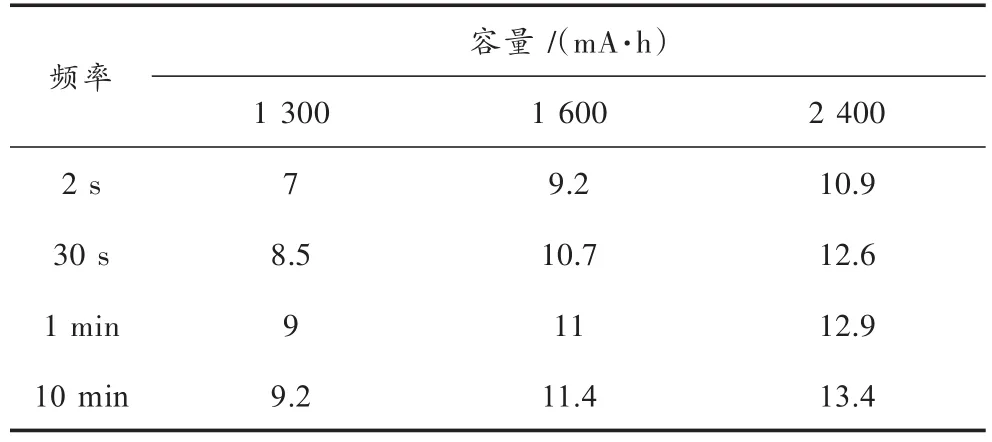
表1 节点生存时间 d
为了提高节点的生存时间,Wendi Rabiner Heinzel⁃man等人在2000年最早提出了一种低功耗自适应集簇分层型协议——LEACH算法[2⁃5],其主要思想是聚类
内所辖的节点以TDMA的方式分时向类首传输数据,数据经类首汇聚压缩后,再向目的节点发送,且只有类首进行数据传输,这种方法导致WSN节点的能耗不均衡,最终会降低WSN的生存时间。美国南加州大学的Yong⁃gang ferry Zhao、加利福尼亚大学的Deborah Esrtin等人设计了一种eScan方法[6]来监视传感器的能量剩余情况,通过减少能量较少的节点的采样次数达到节点能耗一致,但是,此种方法又降低了节点的采样精度。
基于以上原因,提出了一种基于曲线拟合的插值算法,该算法延长了节点的生存时间,提高了节点的观测精度。
1 算法分析
实际测得的数据往往为离散的数据,而这些离散的数据无法满足高精度数据的需求,因此,插值算法的优点就得到了极大体现,插值算法的基本思想是:
(1)根据之前数据的走势来估计未采集数据的值;
(2)根据已经测得的离散数据点的值来估计通过这些数据点的曲线公式。
通过减少系统的工作时间来提高WSN电池单次充电后的使用时间。若采用此方法,则采样系统数据时会出现部分采样盲区,为了解决采样盲区的问题引入牛顿插值算法[7⁃8]。
目前,常用的插值算法有牛顿插值算法、埃尔米特插值算法、三次样条插值算法和分段插值算法。由于文中的采样点并非一成不变,往往需要在原有数据的基础上添加一些数据节点,而且,根据n次代数插值问题的解存在且惟一这一定理可知,具有递推特性的牛顿插值算法最为合适用来解决此类问题。
2 曲线拟合
2.1最小二乘曲线拟合[9⁃10]的基本原理
通常来讲,数据拟合问题可以用表2中的表达式来表示。

表2 离散数据表
根据离散数据表,计算拟合函数:

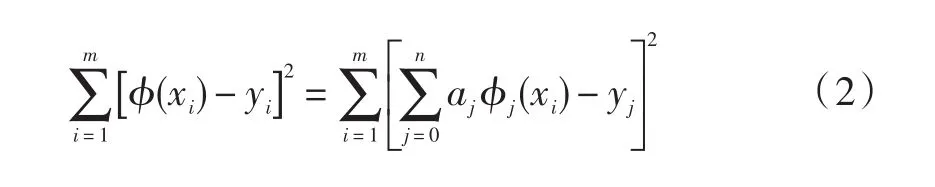
使得:达到最小,这里的函数ϕ(x)称为拟合函数,称式(2)为拟合条件。
一般来讲,ϕ0(x),ϕ1(x),…,ϕn(x)是给定的函数。通常将式(2)作为拟合准则,然后确定式(1)中的各项系数a0,a1,…,an。由于式(2)具有线性方程的形式,因此,这类拟合问题被称为数据拟合的线性模型。通常为了确定数据的拟合问题,首先需要选取合适的函数类{ϕ0(x),ϕ1(x),…,ϕn(x)}。例如选取幂函数类{1,x,x2,…,xn},则:
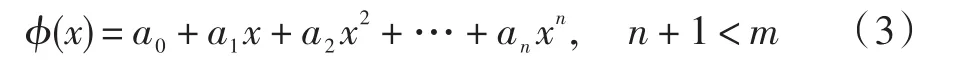
式(3)称为多项式的拟合函数。
2.2拟合函数参数的确定
设函数{ϕ0(x),ϕ1(x),…,ϕn(x)}已经确定,根据拟合条件式(2)确定拟合函数式(1)中的各项系数a0,a1,…,an的方法称为最小二乘法,拟合函数与数据表中函数在该点上的差值为:
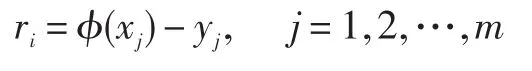
组成的向量称为残差,记为:
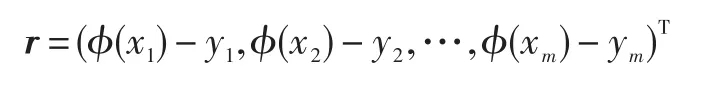
残差向量r的分量平方和为:
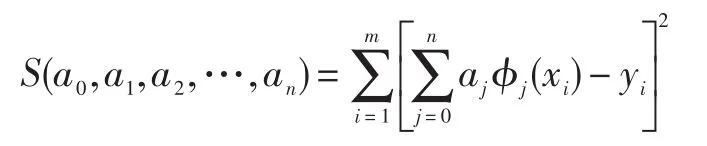
这是一个以a0,a1,…,an为自变量的非负二次函数。所以,根据拟合条件式(2)导出一个二次函数的最小值问题,即确定a0,a1,…,an使残差平方和最小。为了求S(a0,a1,…,an)的最小值点,令:

即:
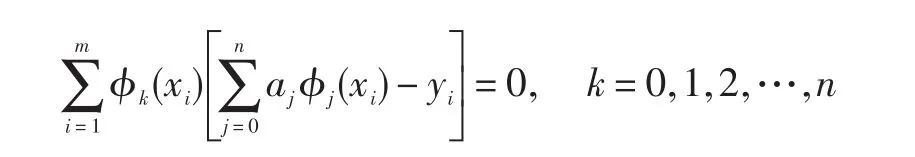
由于a0,a1,a2,…,an是未知数,将上式整理为:
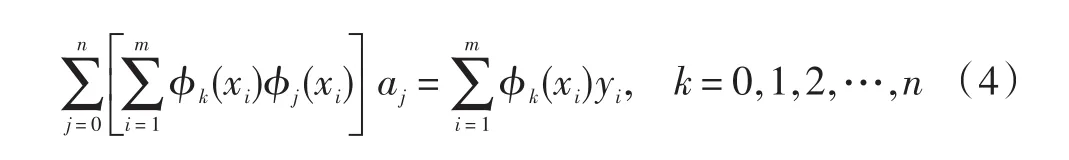
式(4)称为正规方程组,由它的解a0,a1,a2, …,an可以确定拟合函数:
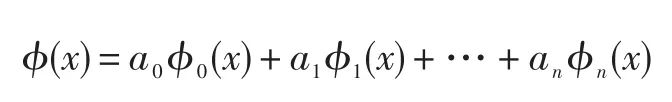
3 应用与测试
3.1原始数据
通过实地测量,采集了一个月的温度数据,从这一个月数据中随机抽取一天的温度数据,如表3所示。

表3 不完整的全天采样温度数据 ℃
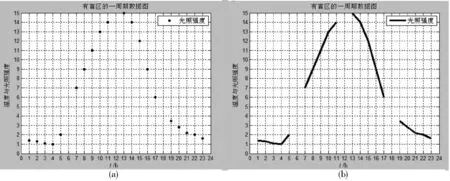
图1 原始采样数据
由图1可以看出,图中有明显的空缺,不利于观测者观察,采集温室数据主要是为了针对该数据做出相应的调整,如温室温度过低,则提高温室的温度,因此,采样数据对于温室的调控至关重要,残缺的数据不利于温室调控,因此,下文便是如何将残缺的数据补全。
3.2通过牛顿插值算法获取采样盲区数据
根据牛顿插值公式,在Matlab中编写M函数实现牛顿插值公式,首先在M文件中建立function函数,func⁃tion s=Newtonfun(x,y,t),在Matlab中通过function函数计算插值,通过牛顿插值法得到的盲区数据如表4所示。
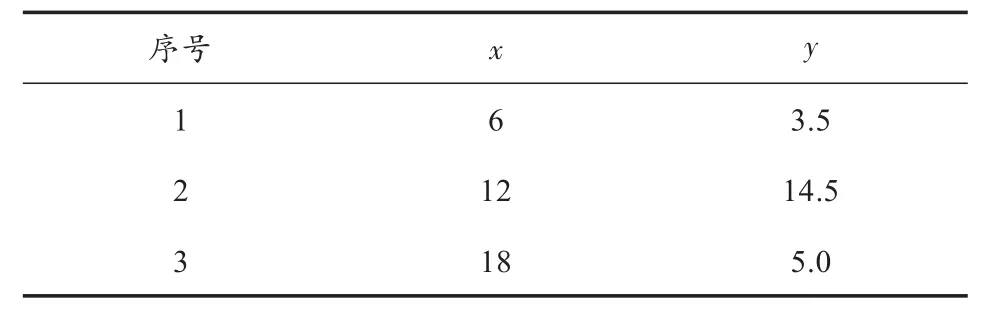
表4 盲区数据
3.3插值函数处理后的数据
将表4中的数据补充到表3中,得到的表格见表5。

表5 完整的全天采样数据 ℃
由插值算法处理后的数据,经Matlab软件绘制的曲线图形如图2所示。
1.2 方法 对119名发生血源性暴露医务人员的人群分布、暴露方式及部位、暴露源种类、暴露后处理方式、预防用药及结果等情况汇总分析。

图2 经插值算法处理后的数据
图2(a)中的数据是由离散的点组成的,其主要特点是全天24 h每个小时采样一次数据,且每小时只能得到一次观测数据,因此该数据精度有限,且该数据为离散的数据,不利于观察。于是测得了第一天0.75天到第二天的0.25天的数据,并将其组合为一个周期,其图形如图2(b)所示,与图2(a)相比,图2(b)明显更方便观察。
3.4通过曲线拟合的最小二乘法求取温度曲线函数
温室大棚的温度在一天中的温度变化如表5所示,随着时间的变化,其温度值也不断的改变,通过Matlab将其温度值描成一条线,如图2(b)所示,可以近似地将其看作是抛物线,则可以将其公式设为:
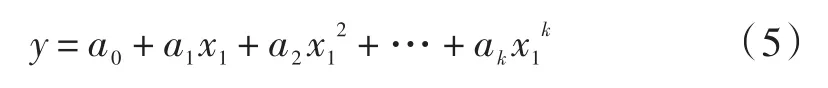
其中:y为温度,xn(n =1,2,…,k)为时间样本,在二维平面中,x轴表示时间,y轴表示温度,随着时间的变化,温度也在不断变化;k为取样的次数;a为未知参数。对于n组观测值,每组观测值都为已知,则若要求出以上函数公式,则需要求出公式中的未知参数a,在本文中运用最小二乘法求取各未知参数a的值。
由式(5)可知,随着x的次数越来越高,含a的项也会越多,计算起来也会越复杂,而且其计算结果也会相应的更加不准确。本文中,在一天之内的温度变化如图3所示,一天之内温度曲线的大体走向如同正弦曲线,但是,在前半部分的时间与后半部分所占的时间却不相同。因此,不能将正弦曲线的公式应用到本文中。
在本文中,把该曲线的前半部分和后半部分分别作为一个整体,其形状近似为抛物线,但两个抛物线的开口方向相反。设该曲线的前半部分函数为:

前半部分的采样数据如表6所示。
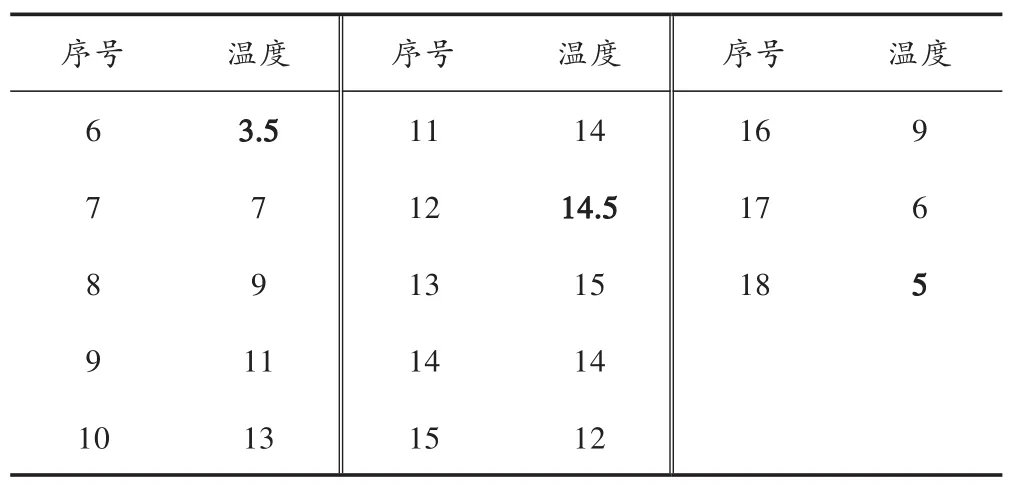
表6 6~18 h的温度数据 ℃
结合表6数据,通过曲线拟合方法可以得到以下参数值:

将a1,a2,a3代入到式(6)得:
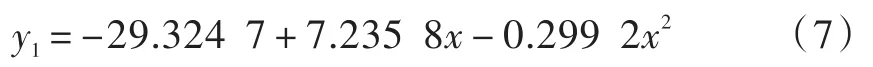
通过同样的方法可以求得该曲线后半部分的公式为:

3.5通过最小二乘曲线拟合方法拟合温度曲线
由式(7),式(8)可画出如图3中纯线条的曲线。将该曲线与实际测得的数据进行对比,将实际数据用带*的线条表示即为图3所示曲线。经过对比发现,拟合的曲线与实际测得的数据曲线吻合度较高。
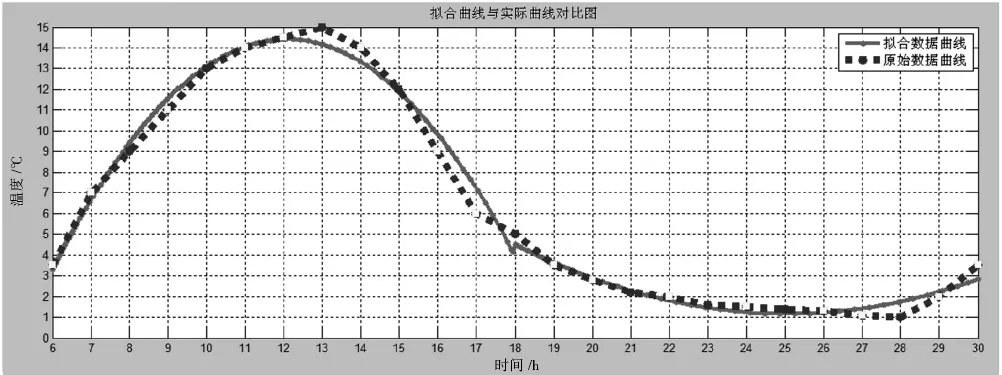
图3 拟合曲线效果图
4 结语
运用最小二乘算法对采样数据的下一个数据点的数据进行预测,但由于采样数据的频率不高,因此采样得到的数据精度不是非常高。文中引入了曲线拟合的插值算法对预测到的数据进行插值分析,从而大大提高了预测数据的精度,为解决无线传感器休眠时工作盲区的数据采样与节能问题提供了理论基础。
参考文献
[1]吕涛,施伟斌,范坤坤,等.WSN节点电池供电性能测试研究[J].传感技术学报,2013,26(10):1457⁃1462.
[2]贾云杰.基于LEACH的无线传感器网络分簇路由算法的研究与改进[D].武汉:华中师范大学,2013.
[3]林楠,史苇杭.无线传感器LEACH算法的优化及仿真[J].计算机仿真,2011(1):178⁃181.
[4]张志艳.无线传感器网络LEACH路由算法研究与改进[D].成都:西南交通大学,2014.
[5]赵雁航.一种基于LEACH协议改进的物联网路由算法[D].长春:吉林大学,2014.
[6]苏兵,许文慧.无线传感网剩余能量监测算法研究[J].科学技术与工程,2014(3):235⁃238.
[7]张菊丽,王新民,张举中.基于牛顿插值算法的模糊控制器[J].模糊系统与数学,2007(2):87⁃91.
[8]马飞,华继学,吴静.遗传牛顿插值算法在地形可视化中的应用[J].空军工程大学学报(自然科学版),2007(5):87⁃90.
[9]倪慧,李重,宋红星,等.带插值条件的移动最小二乘曲线拟合[J].浙江理工大学学报,2011(1):135⁃139.
[10]齐林,张芳,陈恩庆.基于移动最小二乘曲线拟合的LFM信号参数估计[J].郑州大学学报(工学版),2011(3):95⁃98.
Research on interpolation algorithm based on curve fitting for energy consumption of WSN
HUANG Xingli1,2,MU Dejun1,LI Zhe1,3,JIAO Litao1,Huang Yijie1
(1. College of Automation,Northwestern Polytechnical University,Xi’an 710072,China;2. College of Business,Wenzhou University,Wenzhou 325035,China;3. College of New Technology,Hubei Engineering University,Xiaogan 432000,China)
Abstract:Since the sensor nodes of WSN mainly depend on battery to supply power,have short survival time and low ob⁃servation accuracy,the interpolation algorithm based on curve fitting is proposed according to the research result of WSN energy consumption. The sampling frequency is reduced by the algorithm to simulate the reduced data,and the function formula ap⁃proach to the sampling data point is fitted by using curve fitting method. This method can prolong the survival time of sensor nodes,and improve the sampling precision indirectly.
Keywords:WSN;curve fitting;interpolation algorithm;sampling
作者简介:黄兴利(1981—),在读博士,讲师。主要研究方向为网络控制与信息安全。
基金项目:2014年浙江省自然科学基金(LY14F020030);2015年浙江省科技厅公益项目
收稿日期:2015⁃06⁃17
doi:10.16652/j.issn.1004⁃373x.2016.01.003
中图分类号:TN926⁃34
文献标识码:A
文章编号:1004⁃373X(2016)01⁃0009⁃04
