“高分四号”卫星影像辐射与几何精度评价
2016-02-23徐文龙小祥李庆鹏崔林钟慧敏
徐文 龙小祥 李庆鹏 崔林 钟慧敏
(中国资源卫星应用中心,北京 100094)
“高分四号”卫星影像辐射与几何精度评价
徐文 龙小祥 李庆鹏 崔林 钟慧敏
(中国资源卫星应用中心,北京 100094)
“高分四号”(GF-4)卫星是中国首颗高分辨率静止轨道面阵凝视光学遥感卫星,载荷首次采用面阵CMOS探测器在36 000km高轨成像、基于面阵成像构建在轨相对辐射校正模型、面阵相机光学畸变在轨检校。文章首先分析了影响GF-4卫星影像辐射质量(quality,以下同)与几何精度的关键因素,然后介绍了高轨面阵成像处理模型的构建技术,最后分析评价了GF-4卫星影像的辐射质量、几何质量和处理精度。结果表明:GF-4号卫星全色多光谱影像的平均行标准差、平均标准差和广义噪声等相对辐射精度指标均优于3%,典型地物信噪比平均优于40dB。影像内部畸变在垂轨和沿轨方向均优于0.8个像素。
相对辐射校正 几何精度分析 面阵相机在轨几何检校 “高分四号”卫星
0 引言
“高分四号”(GF-4)卫星是我国首颗高分辨率静止轨道光学遥感卫星,卫星搭载一台凝视相机,该相机同时具有可见光近红外(VNIR)成像通道和中波红外成像通道。VNIR影像幅宽优于500km,IRS影像幅宽优于400km,可以实现高时间分辨率和高地面像元分辨率相结合,具有凝视成像、机动巡查、区域成像等多个模式,能够满足减灾、气象、地震、林业等多个领域的不同需求。
遥感卫星产品质量(quality,全文同)主要包括影像辐射质量和几何质量两个方面,其中影像的辐射质量是图像质量的先决条件,其不仅决定了影像色彩响应均衡一致性,也影响后续用户定量反演、影像融合等应用;影像的几何质量是图像质量最重要的因素,它不仅决定了影像的内部几何精度和外部定位精度,也影响后续用户区域网平差、变化检测等应用。
GF-4卫星首次采用面阵CMOS探测器在36 000km高轨成像,而面阵成像的在轨相对辐射校正模型构建、面阵相机光学畸变检校均尚属首次,GF-4卫星影像产品处理后辐射质量和几何质量能否满足用户需求是亟待解决的问题,所以必须开展GF-4卫星影像辐射与几何精度评价分析工作。
1 影像辐射质量评价分析
1.1 影像辐射质量影响关键因素
卫星发射前后,由于发射过程和在轨空间环境的影响,相机各波段的底电平输出、响应特性都可能发生变化,使得根据地面整星定标数据获得的定标系数与相机真实响应曲线之间存在误差。从而导致在轨图像数据经地面相对辐射定标系数进行辐射校正后,存在影像响应不一致现象。对影像的辐射质量进行分析评价可以在一定程度上反映卫星成像质量,有助于确定卫星影像在各应用领域中的处理方法和方案[1-2]。为了准确分析GF-4卫星影像辐射特性,结合GF-4卫星传感器特点,本文从相对定标精度和信噪比两个方面对影像辐射质量的主要影响因素进行阐述。
1)相对定标精度。相对辐射定标是确定场景中各像元之间、各探测器之间、各波段之间以及不同时间测得的辐射量的相对值,从而消除由于探测器在空间上的响应不一致、在时间上的不稳定性,以及电路噪声所引起的非均匀性辐射失真[3-4]。
2)信噪比。信噪比通常定义为图像中的有用信息与噪声信号的比值。在复杂地物区域,由于信号的复杂性,通常难以可靠地区分有用信息与噪声,因此常选用均匀地物区域进行信噪比测试。图像信噪比越大,说明混在图像信息中的噪声越少,有效信息抗噪能力越强,图像质量越好[5]。
1.2 基于面阵相机的在轨相对辐射校正与处理模型构建
目前,线阵推扫 CCD相机一般采用基于实验室辐射定标数据与卫星在轨数据概率密度统计相结合的方法来构建相对辐射校正模型[6-7]。
而对于面阵成像,在轨成像过程中无法获取具有统计意义的探测数据。在轨如何优化从而构建精确的辐射校正模型,成为影响GF-4卫星图像相对辐射校正精度和外场绝对定标精度的关键。
本文采用基于不同卫星同步过境、模拟不同卫星成像几何进行交叉定标,同步进行几何定标和相对辐射模型定标的技术方法。该方法采用“高分一号”(GF-1)卫星与GF-4卫星同步过境同时成像时,以GF-1卫星16mWFV相机的几何模型为参考,构建GF-4卫星同步过境时刻的内外方位元素检校模型,然后以此时刻的严格几何模型为基准,构建GF-1与GF-4卫星的几何关系;根据几何关系实现GF-1卫星影像在GF-4卫星焦平面的成像模拟,从而构建GF-4卫星在轨相对辐射校正模型。总体技术流程如图1所示。
1.3 辐射质量评价方法
1.3.1 相对辐射校正精度评价方法
相对定标精度反映了各探元的响应特性。相对定标精度越差,说明相机各探元的辐射差异越大。本文主要从平均行标准差、平均标准差和广义噪声三个方面对相对定标精度进行分析和评价。具体步骤为:1)选择数据处理系统生产的沙漠、深海、山地、平原、农田等均匀地物的GF-4卫星1级图像。2)选择均匀样板区,测量图像相对定标精度。均匀样板区域的选择在目测均匀的前提下选择的列应尽可能大。3)对以上选择的图像分别采用平均行标准差法、平均标准差法和广义噪声法评价相对辐射校正精度[8-9]。
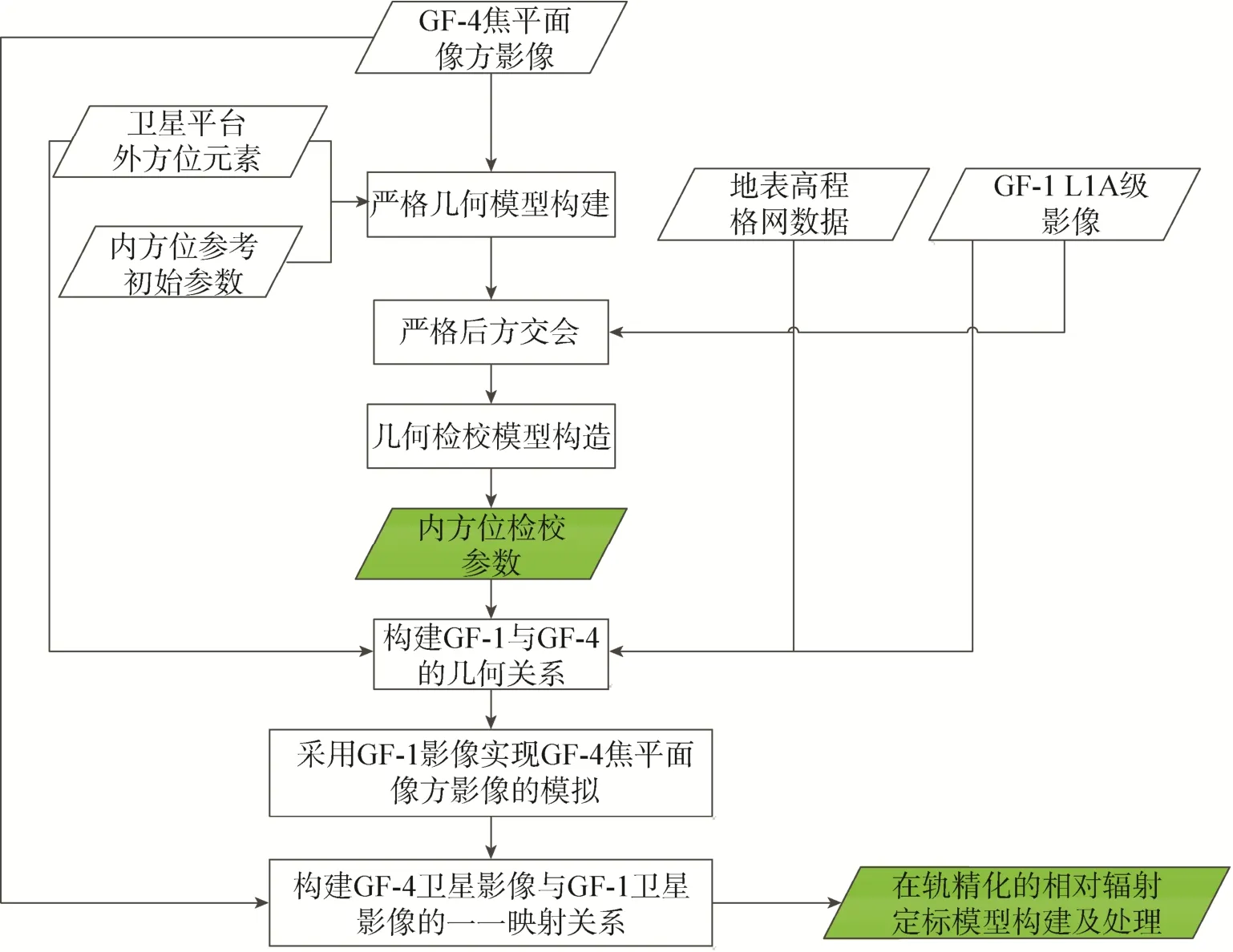
图1 GF-4卫星在轨相对辐射校正与处理技术流程Fig.1 The in-orbit relative radiometric correction and processing technical flow of GF-4 satellite
(1)平均行标准差法
首先,计算相对辐射校正后图像每列的平均值,得到一个平均行,然后,计算该行数据的标准差,再除以整幅图像的平均值,即为通过该图像计算得到的相对定标精度。即
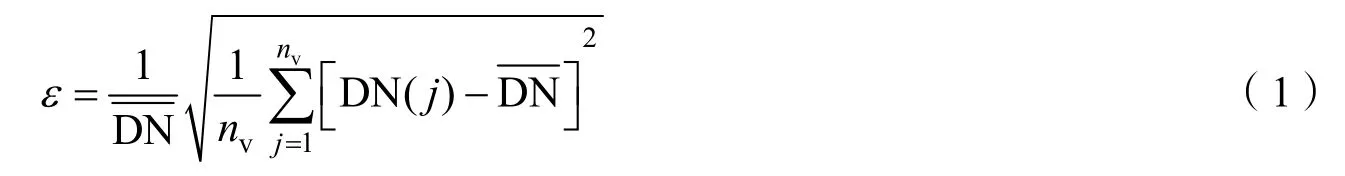
式中 ε为相对定标精度;nv为CMOS器件垂轨方向探元个数;DN(j)为图像上第j探元的DN值;DN为整幅图像DN值的均值。
(2)平均标准差法
首先,对相对辐射校正后图像的各行计算其标准差,然后,除以该行的平均值,得到各行的校正精度,取其平均值即为该图像计算得到的相对定标精度。即
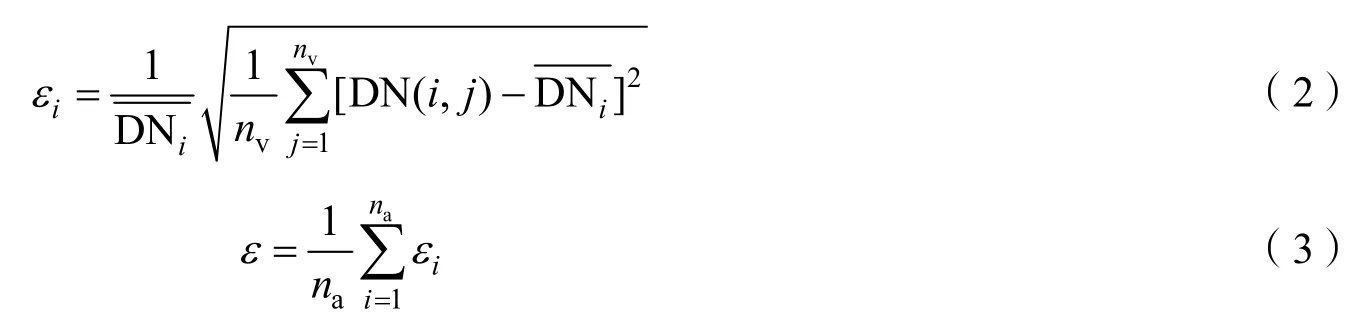
式中 εi为图像第i行的相对定标精度;DNi为图像第i行DN均值;na为CMOS器件沿轨方向探元个数;DN(i,j)为图像第i行j列探元的DN值。
(3)广义噪声法
相对定标精度的计算公式为

1.3.2 信噪比评价方法
图像噪声评价主要包括能量分配和辐射精度的评价,反映各波段整体的明暗和针对不同辐亮度的地物的能量分配以及数字图像对微小细节反差的表达能力[10]。
信噪比是图像中的有用信息与噪声信号的比值。图像的信噪比越大,说明图像中有效信息相对于噪声干扰越强,即遥感图像反映的地物信息更好,图像像质好。信噪比近似决定了图像有效信号的比例,采用方差法:选择图像中的一块均匀区域,计算该区域响应值的均值和方差,并将均值和方差之比作为信噪比[11]。具体测试方法如下:
1)对于具有不同反射率的地物,成像系统的噪声对于图像的影响程度有所不同。为了全面测试成像系统的噪声特性,按照反射率对地物进行分类,对于获取的遥感图像来说,即按照图像的表观DN值将其分为三类:高反射率地物、中反射率地物和低反射率地物。
2)针对以上三种类型地物,选取图像中具有大范围、均匀、高、中、低反射率地物区域,分别计算信噪比。高、中、低反射率地物区域选取原则为:高反射率地物区域的平均DN值与图像均值的绝对值差大于一倍标准差;中反射率地物区域的均值与图像均值差的绝对值小于一倍标准差;低反射率地物区域的均值与图像均值的绝对值差大于一倍标准差。
2 影像几何质量评价分析
2.1 影像几何质量影响关键因素
GF-4卫星是国内第一颗面阵凝视成像卫星,由于高轨环境复杂,传感器内部温差变化剧烈,其几何模型不同于传统的 CCD线阵推扫式卫星,也不同于航空面阵传感器几何模型。需结合成像条件及太空环境特点分析影响影像几何质量的因素,本文从安装角误差和相机光学畸变两个方面对 GF-4卫星影像几何质量的主要影响因素进行了阐述。
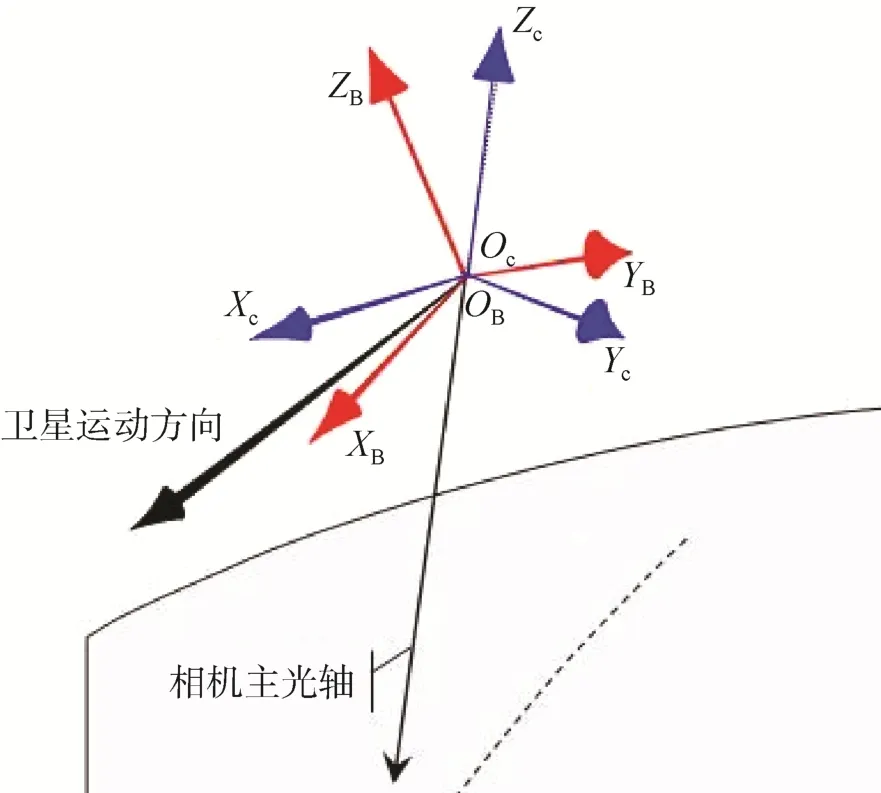
图2 相机坐标系与卫星本体坐标系示意Fig.2 The diagram of camera coordinate system and satellite coordinate system
(1)安装角误差
GF-4号卫星在轨成像时,由于星敏、陀螺等姿态测量仪器获取的是卫星本体坐标系在惯性空间坐标系下的姿态角,因此,理想情况下,将相机安装在卫星上时,相机坐标系与卫星本体坐标系三轴方向应该严格一致,两个坐标系之间的旋转矩阵应为单位矩阵,三轴夹角均为 0°。然而,在实际装调过程中两个坐标系三轴间总存在着角度差,这称为相机安装角误差。如图2所示,Oc-XcYcZc和OB-XBYBZB分别为相机坐标系与卫星本体坐标系。在卫星发射前,即使采用实验室检校的方法对相机安装角进行了标定,在卫星发射过程中,由于应力释放、材料出气、空间环境变化等各种因素的影响,相机安装角会发生改变。考虑到卫星高轨成像,角度误差对定位精度影响很大,因此,必须通过在轨几何定标对相机安装角误差进行检校,即确定严格几何成像模型中的相机坐标系与卫星本体坐标系间的旋转矩阵[12-13]。
(2)相机光学畸变
由于高轨空间环境复杂,成像时间段内温度变化剧烈以及发射过程中应力释放等因素的影响,导致相机成像参数(主点、主距、光学畸变等)与地面实验室标定差异巨大,必须定期通过在轨几何定标重新标校,否则,卫星影像产品的几何质量将由于内部几何畸变的存在,受到严重的影响。相机面阵CCD畸变如图3所示。图3中O-XcYcZc为像空间坐标系;曲面dc即为面阵相机的畸变曲面[14-15]。
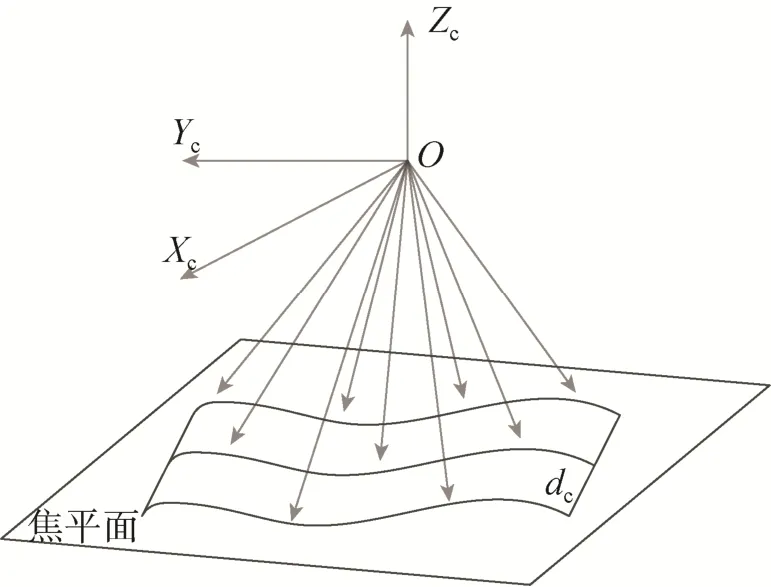
图3 面阵CCD畸变曲面示意Fig.3 The diagram of array CCD sensor distortion curve
2.2 基于面阵相机的在轨几何检校与处理模型构建
描述相机内部畸变的数学模型主要有物理畸变模型与综合模型。物理畸变模型是根据相机成像时存在的各种畸变的物理特性建立的数学模型;典型的光学相机物理畸变模型如布朗模型。该模型的特点在于每个参数都有具体的物理意义,但往往由于待解参数众多导致过度参数化的问题,难以获得稳定、高精度的解。综合模型则不考虑各几何畸变具体的物理意义,而采用一种数学意义上的经验模型综合描述各种几何畸变的影响,实质是对几何畸变曲面(面阵相机)的一种拟合[16]。
GF-4卫星采用面阵CMOS探测器成像,其视场角较小,焦距较长,因此其几何畸变曲线相对简单,主要反映为低阶畸变(如平移、旋转、缩放、主距变化、低阶径向畸变等),高阶畸变很小,基本可以忽略不计;另外,高轨窄视场角的成像特性使得相机内部各参数之间,以及相机内部参数与外方位元素之间都具有很强的相关性[17-18]。基于以上考虑,本文采用基于二维三次多项式曲面探元指向角模型拟合CMOS每个探元光轴指向角,计算公式为
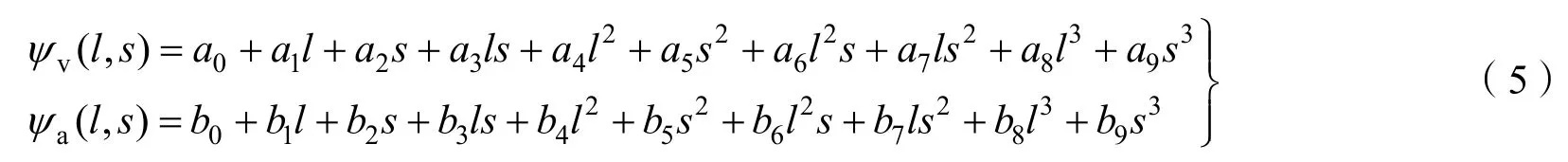
式中 ψv(l, s)、ψa(l, s)分别为垂轨方向和沿轨方向上的光轴指向角;a0~a9,b0~b9为内检校参数;l、s表示影像上像点坐标的行、列号。此外,考虑到温度对于影像的定位精度存在一定的影响,外定标模型改进为随温度变化的相机安装角模型,即通过统计不同地区、不同太阳高度角条件下相机安装角随温度变化关系,通过一定的数学模型进行建模和求解,从而获取相机安装角误差补偿模型[19]。
根据共线方程,构建卫星在轨几何检校模型为
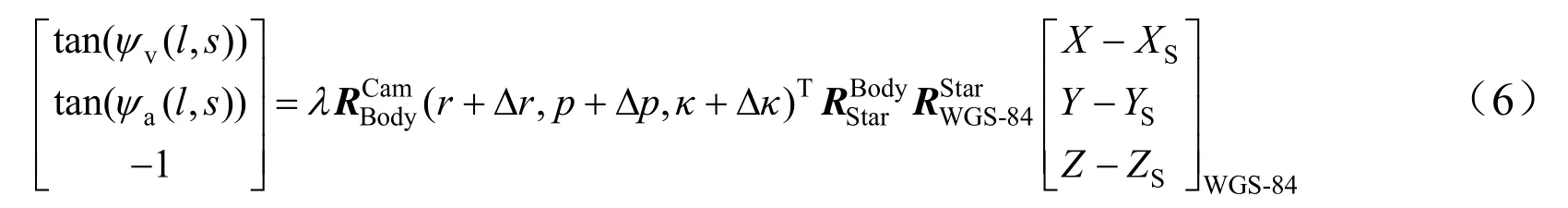
在该模型下,要检校包括a0~a9,b0~b9的20个系数、3个安装角(r,p,κ),以及安装角随温度变化关系(Δr,Δp,Δκ)。可将这些参数划分为内外检校参数,其中内检校参数(a0~a9,b0~b9)用于确定相机内部CMOS各探元在相机坐标系下的坐标;外检校参数r、p、κ,Δr、Δp、Δκ用于恢复相机坐标系在空间中的位置和姿态。将内外检校参数分步处理,即利用分步检校方法解算内外检校参数,其原理为:首先解算外检校参数,恢复相机坐标系在空间中的姿态;然后在此基础上解算内检校参数,确定CMOS各探元在相机坐标系下的位置坐标,迭代解算直至结果收敛[20]。其技术流程如图4所示。
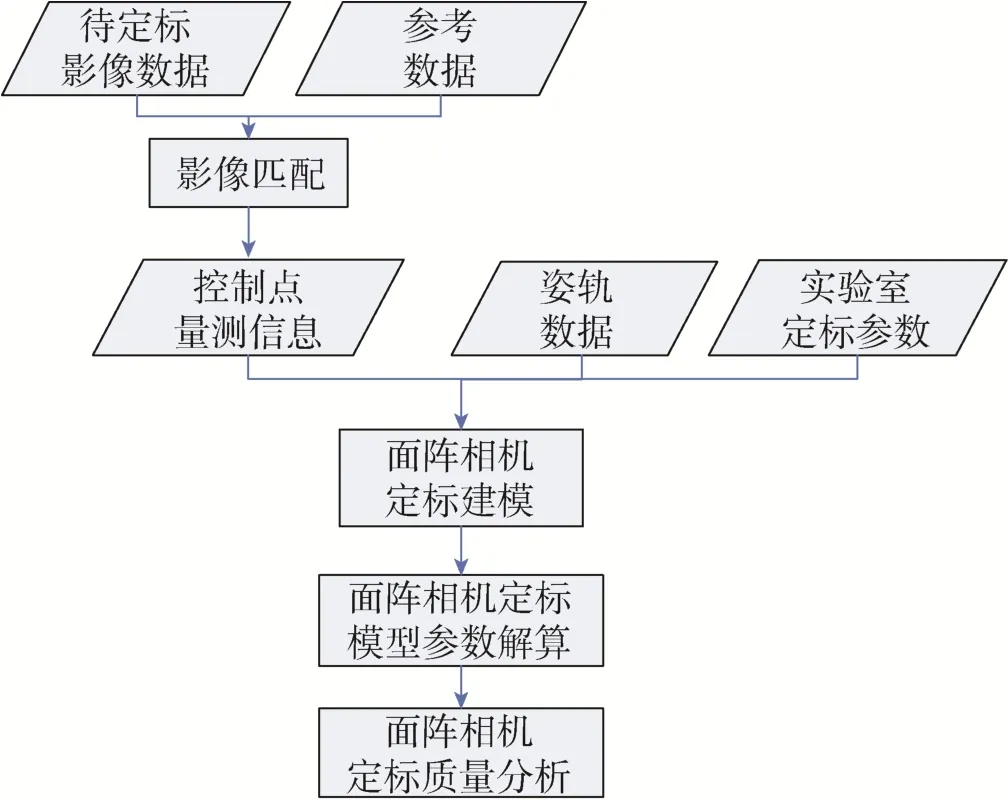
图4 面阵相机在轨几何检校与处理模型构建技术流程Fig.4 Array camera in-orbit calibration and processing model construction technical flow
2.3 几何质量评价方法
光学遥感影像的几何质量主要体现在影像的内部几何精度与平面定位精度两个方面,其中平面定位精度表征影像上给定点的地理位置与其真实位置间的误差,内部几何精度表征影像的变形程度。
2.3.1 内部几何精度评价方法
具体方法如下:
1)对待检影像覆盖范围内的控制点进行人工刺点,假设控制点物方坐标为(B,L,H),人工量测的像点坐标为(s,l);
2)将控制点物方坐标(B,L,H)代入该景影像的 rpc文件中反算得到像点坐标(s', l'),此时像方残差(vs, vl)即为该景影像rpc文件的几何定向精度,

3)统计所有检查点像方残差(vs, vl)的均值(MEANvs,MEANvl)和中误差(RMSEvs,RMSEvl),当检查点满足一定数量要求(一般为 7×7或 9×9均匀格网分布),且在影像范围内均匀分布时,均值(MEANvs,MEANvl)反映了该景影像外部系统漂移误差,即无控定位误差,而单位权中误差(RMSEvs,RMSEvl)则能够定量表征该景影像内部几何精度,计算公式为:

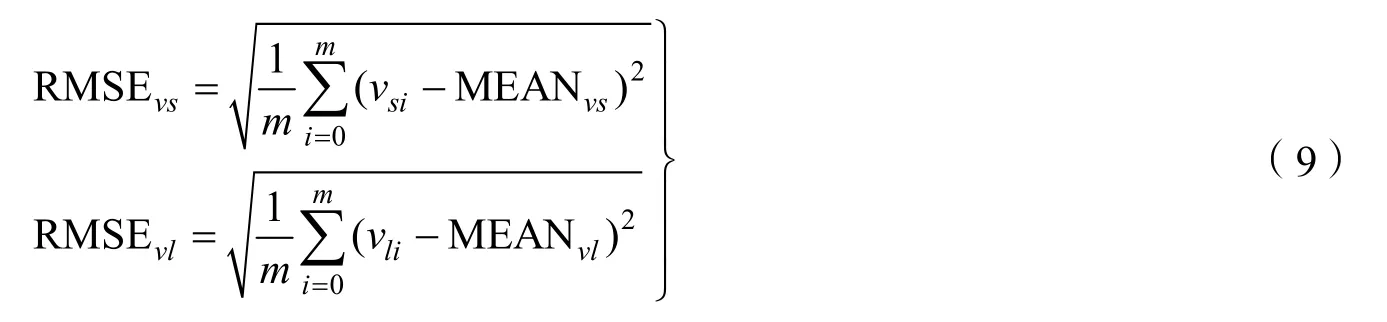
式中 vsi,vli分别表示第i个控制点在列方向和行方向的像方残差;m为控制点数量。
2.3.2 平面定位精度评价方法
首先,在经过系统几何校正的图像上,利用数据评价软件自动选取待评图像和参考图像的控制点(GCP),然后计算出GCP在待评图像和参考图像的实际地理坐标差值,最后,统计多景图像的GCP位置误差值的平均误差和均方差作为图像的定位误差。
测试具体流程为:
1)选取多景清晰、成像质量良好的图像作为测试图像。
2)对选取图像进行2级产品生产。
3)查找参考图像,并对参考图像进行投影转换、镶嵌等处理。
4)对每幅图像自动选点,计算出GCP的图像坐标。
5)对GCP点进行筛选,获得均匀分布的36个控制点。
6)计算 GCP在待评图像和参考图像的实际地理坐标差值,,其中,ΔX=X图像-X真实,为GCP在待评测图像和参考图像上WGS84坐标系下的东西向和南北向平面投影坐标。
7)计算二级图像产品上所有GCP地理坐标差值的均值E,即为该景影像的外部定位精度。均值计算公式为:,其中,m为GCP点的数量,Di为第i个GCP在待评图像和参考图像的实际地理坐标差值。
8)分别计算每个传感器全部产品定位精度的平均误差和均方差,即得到每个传感器总的二级图像产品几何定位精度。
3 测试结果与分析
本文选取覆盖沙漠、海洋、农田、山地以及平原的5景GF-4卫星VNIR影像进行影像辐射质量评价分析;选取8景不同时相、不同区域的VNIR影像进行内部几何精度评价分析;选取20景不同时相、不同区域的影像来验证其平面定位精度,其中,内部几何精度评价和平面定位精度评价所用参考 DOM影像分辨率16m、精度优于16m,参考DSM影像分辨率30m、精度优于20m。
3.1 影像辐射质量测试结果
3.1.1 相对辐射校正精度测试结果
本次试验选取系统生产的天气晴好、能见度高、无云的5景GF-4卫星1级影像数据进行相对辐射校正精度评价,成像区域主要为沙漠、海洋、农田等地物,各波段评价结果如表1所示。
测试结果表明可见光波段的相对辐射校正精度评价中平均行标准差、平均标准差和广义噪声等各项指标均优于3%,满足研制总要求。
3.1.2 信噪比测试结果
本次试验系统生产的天气晴好、能见度高、无云的另5景GF-4卫星1级影像数据进行信噪比测试,成像区域主要为海洋、沙漠等均匀地物,测试结果如表2所示。
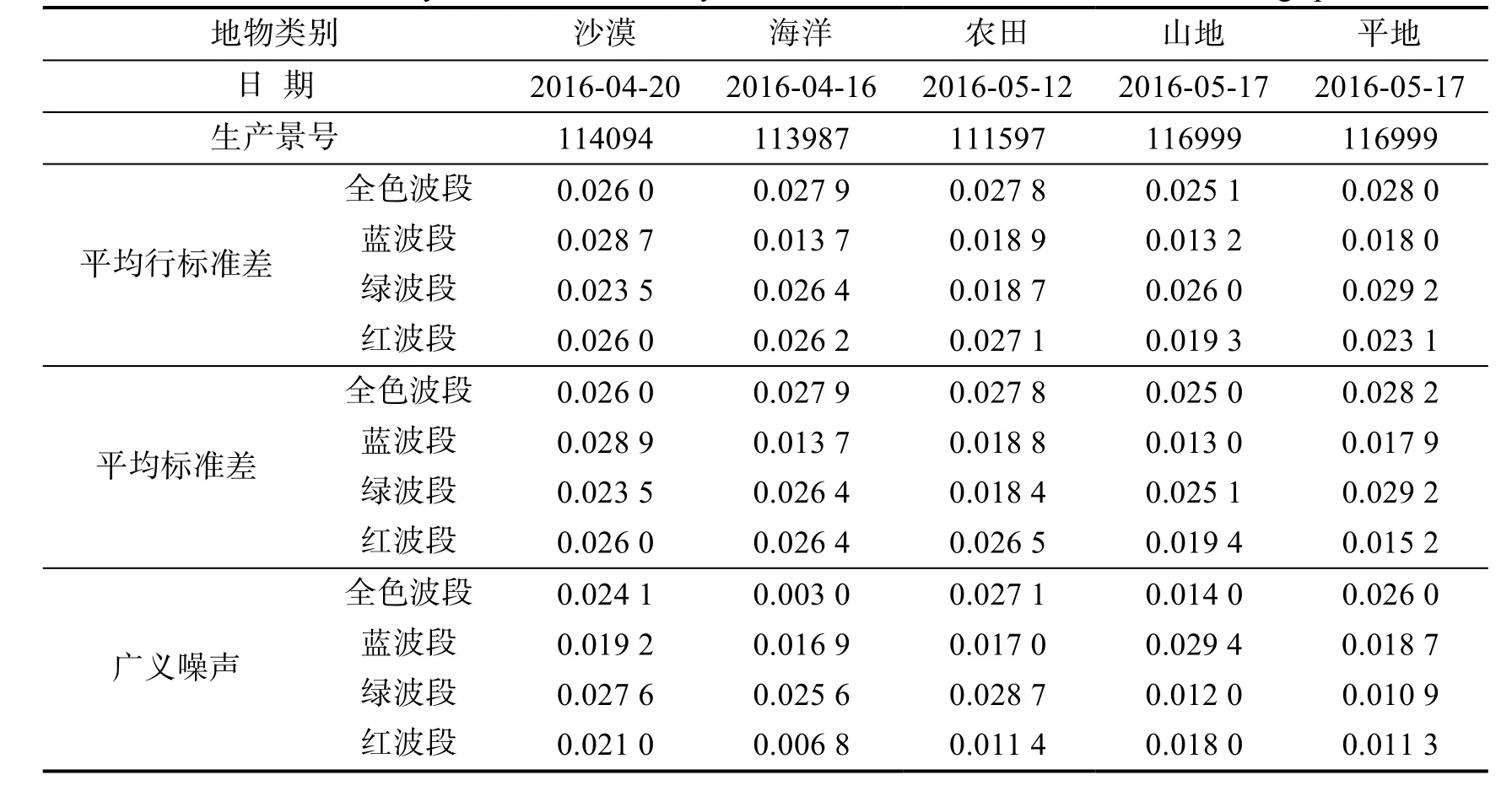
表1 各波段相对辐射校正精度评价结果Tab.1 The result of accuracy evaluation and analyzes of relative radiometric correction among spectral bands
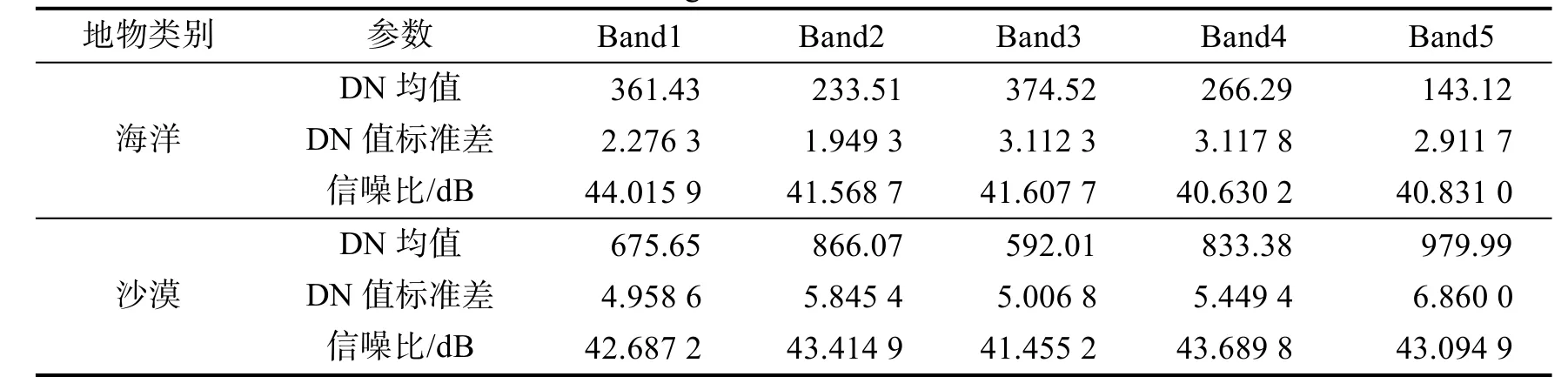
表2 “高分四号”卫星相机信噪比评价结果Tab.2 The evaluation result of signal-to-noise ratio for the camera of GF-4 satellite
测试结果表明GF-4卫星VNIR影像典型地物信噪比平均优于40dB,满足研制总要求。
3.2 影像几何质量测试结果
3.2.1 影像内部几何精度测试结果
选取8景不同时相、不同区域的VNIR影像进行内部几何精度评价分析,内部几何精度统计如表3所示。
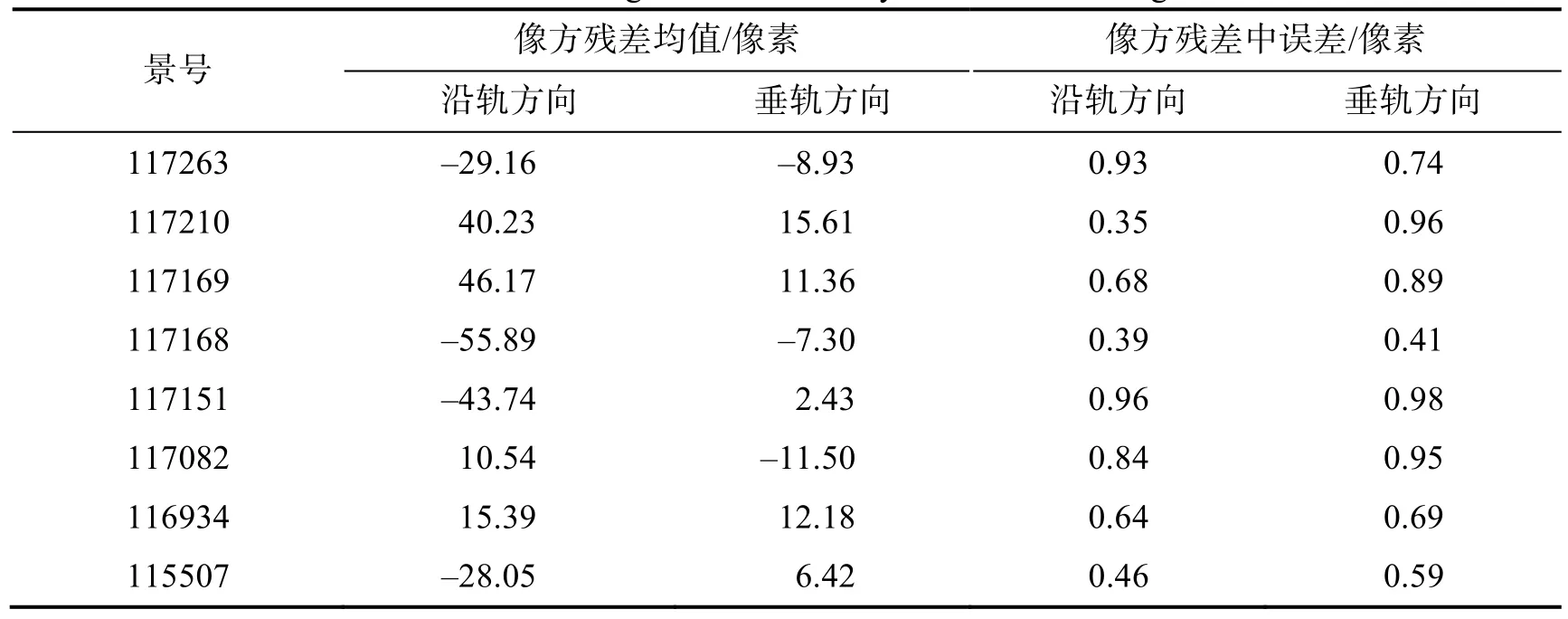
表3 GF-4卫星VNIR影像内部几何精度测试结果Tab.3 The test result of internal geometric accuracy for the VNIR image of GF-4 satellite
根据表3的测试结果,可计算出VNIR影像的内部畸变在垂轨方向像方残差均值为0.66个像素,方差为0.22个像素;沿轨方向为0.78个像素,方差为0.19个像素。表明在轨几何检校后内部畸变在沿轨和垂轨方向均得到了有效补偿。
3.2.2 影像平面定位精度测试结果
VNIR影像平面定位精度测试结果如表4所示。
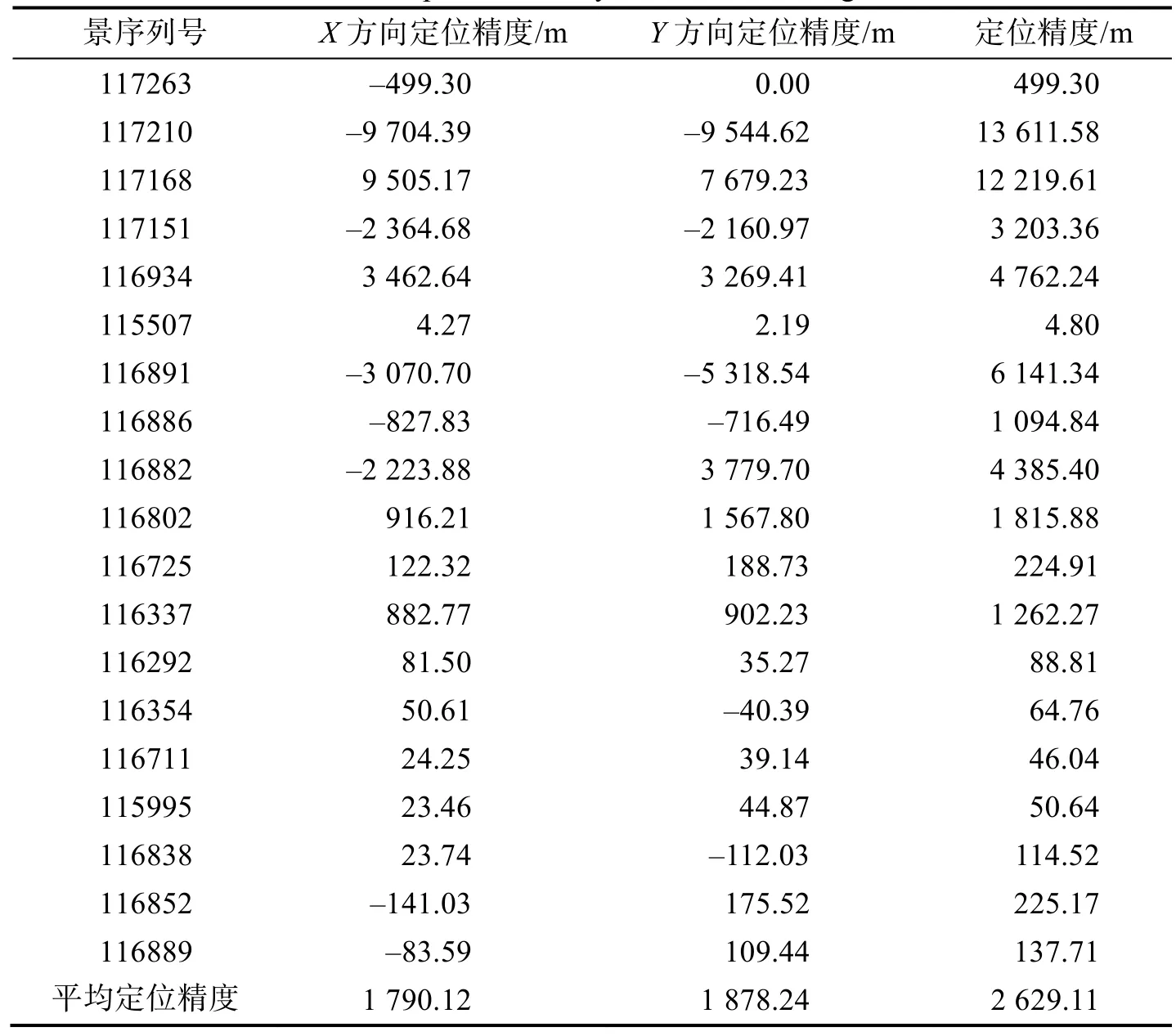
表4 GF-4卫星VNIR影像平面定位精度测试结果Tab.4 The test result of plane accuracy for the VNIR image of GF-4 satellite
根据表4可知,VNIR影像平面定位精度均值为2 629.11m,标准差为3 971.20m,满足研制总要求。
4 结束语
本文首先对影响 GF-4卫星影像辐射质量与几何精度的关键因素进行了分析,然后介绍了高轨面阵成像处理模型的构建技术,最后对 GF-4卫星影像的辐射质量、几何质量和处理精度进行了分析评价。实验结果表明:GF-4号卫星VNIR影像的平均行标准差、平均标准差和广义噪声等相对辐射精度指标均优于3%,典型地物信噪比平均优于40dB。影像内部畸变在垂轨和沿轨方向均优于0.8个像素,表明在轨几何检校后内部畸变在沿轨和垂轨方向均得到了有效补偿。
References)
[1] CRESPI M, COLOSIMO G, DE VENDICTIS L, et al. GeoEye-1: Analysis of Radiometric and Geometric Capability[C]// SITHAMPARANATHAN K, MARCHESE M, RUGGIERI M, et al. Personal Satellite Services: Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering. Rome, Italy: Springer Berlin Heidelberg, 2010, 43: 354-360.
[2] 李德仁, 郑肇葆. 解析摄影测量[M]. 北京: 测绘出版社, 1992.
LI Deren, ZHENG Zhaobao. Analytical Photogrammetry[M]. Beijing: Surveying and Mapping Press, 1992. (in Chinese)
[3] 潘志强, 顾行发, 刘国栋, 等. 基于探元直方图匹配的CBERS-01星CCD数据相对辐射校正方法[J]. 武汉大学学报(信息科学版), 2005(10): 925-927.
PAN Zhiqiang, GU Xingfa, LIU Guodong, et al. Relative Radiometric Correction of CBERS-01 CCD Data Based on Detector Histogram Matching[J]. Geomatics and Information Science of Wuhan University, 2005(10): 925-927. (in Chinese)
[4] 王小燕. 遥感卫星光学相机底电平与相对辐射校正的研究[D]. 北京: 中国空间技术研究院, 2005.
WANG Xiaoyan. A Research of Remote Sensing Satellite Optical Camera Bottom Electric Potential and Relative Radiometric Correction[D]. Beijing: China Academy of Space Technology, 2005. (in Chinese)
[5] 曾涌, 张宇烽, 徐建艳, 等. 中巴资源一号卫星 02星 CCD相机实验室辐射定标算法分析[J]. 航天返回与遥感, 2005, 26(2): 41-45.
ZENG Yong, ZHANG Yufeng, XU Jianyan, et al. Analysis of Laboratory Radiometric Calibration Algorithm of CBERS-02 CCD camera[J]. Spacecraft Recovery & Remote Sensing, 2005, 26(2): 41-45. (in Chinese)
[6] LEBEGUE L, KUBIK PH, GRESLOU D, et al. Using Exotic Guidance for Pleiades-HR Image Quality Calibration[C]//The International Archiver of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Beijing: Chinese Society for Surveying, Mapping and Geoinformation, 2008.
[7] TAO C V, HU Y. Updating Solutions of the Rational Function Model Using Additional Control Points for Enhanced Photogrammetric Processing[J]. Photogrammetric Engineering & Remote Sensing, 2001, 68(7): 715-724.
[8] TAO C V, HU Y. Investigation of the Rational Function Model[C]//Proceedings of ASPRS Annual Conference. Washington D C: American Society for Photogrammetry and Remote Sensing, 2000.
[9] TONOLO F G, POLI D. Georeferencing of EROS-A1 High Resolutionimages with Rigorous and Rational Function Model[C]//High Resolution Mapping from Space 2003. Hannover, Germany: ISPRS Workshop, 2003.
[10] GRODECKI J. IKONOS Stereo Feature Extraction—RPC Approach[C]//Proceedings of ASPRS 2001 Conference. St. Louis, 2001.
[11] WESER T, ROTTENSTEINER F, WILLNEFF J, et al. An Improved Pushbroom Scanner Model for Precise Georeferencing of ALOS PRISM Imagery[C]//ISPRS XXth Congress Proceedings. Beijing: The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2008.
[12] 雷蓉. 星载线阵传感器在轨几何定标的理论与算法研究[D]. 郑州: 解放军信息工程大学, 2011.
LEI Rong. Study on Theory and Algorithm of the In-flight Geometric Calibration of Spaceborne Linear Array Sensor[D]. Zhengzhou: The PLA Information Engineering University, 2011. (in Chinese)
[13] 杨俊峰, 胡莘. 三线阵CCD相机的动态检定[J]. 解放军测绘研究所学报, 1999, 19(2): 17-22.
YANG Junfeng, HU Xin. Dynamic Calibration of Three Line Array CCD Camera[J]. Journal of PLA Institute of Surveying and Mapping, 1999, l9(2): 17-22. (in Chinese)
[14] JACOBSEN K. Geometric Aspects of High Resolution Satellite Sensors for Mapping[C]//Proceedings of the ACSM/ASPRS Annual Convention. 1997, 3: 473-482.
[15] FRASER C S, HANLEY H B, YAMAKAWA T. High Precision Geopositioning from Ikonos Satellite Imagery[EB/CD]. Proceedings of ASPRS 2002 Conference. Washington D C, 2002.
[16] BALTSAVIAS E, ZHANG L, EISENBEISS H. DSM Genereation and Interior Orientation of IKONOS Images Using a Testfield in Switzerland[J]. Photogrammetrie Fernerkundung Geoinformation, 2006, 60(1): 41-54.
[17] BÜYÜKSALIH G, JACOBSEN K. Geometric Aspects of MOMS-2P Three-Line Imagery for Mapping Applications[C]. Annual Meeting of the Remote Sensing Society, RSS2000. Leicester, UK, 2000.
[18] CURRY S, BAUMRIND S, ANDERSON J M. Calibration of an Array Camera[J]. Photogrammertric Engineering and Remote Sensing, 1986, 52(5): 627-636.
[19] 祝小勇, 张过, 唐新明, 等. 资源一号02B卫星影像几何外检校研究及应用[J]. 地理与地理信息科学, 2009, 25(3): 16-18.
ZHU Xiaoyong, ZHANG Guo, TANG Xinming, et al. Research and Application of CBRS02B Image Geometric Exterior Calibration[J]. Geography and Geo-Information Science, 2009, 25(3): 16-18. (in Chinese)
[20] 王慧, 吴云东, 张永生. 面阵 CCD 数字航测相机影像几何拼接误差模型与分析[J]. 测绘学院学报, 2003, 20(4): 257-262.
WANG Hui, WU Yundong, ZHANG Yongsheng. Modeling and Analyzing of Geometric Joint Error for CCD Matrix Images of Digital Aerial Camera[J]. Journal of Institute of Surveying and Mapping, 2003, 20(4): 257-262. (in Chinese)
Image Radiometric and Geometric Accuracy Evaluation of GF-4 Satellite
XU Wen LONG Xiaoxiang LI Qingpeng CUI Lin ZHONG Huimin
(China Centre For Resource Satellite Data and Application, Beijing 100094, China)
GF-4 is the China’s first array staring-imaging optical remote-sensing satellite with high resolution. The payload of GF-4 satellite firstly uses array CMOS sensors and images in the 36 000km high orbit. It is first time to apply in-orbit relative radiometric correction model, and to make in-orbit calibration and geometric correction of array camera optical distortion based on array imaging. This paper firstly analyzes the critical factors in GF-4 satellite image’s radiance quality and geometric accuracy, then introduces a technological method of building the processing model of high-orbit array imaging, and finally analyzes and evaluates the radiance quality, geometric quality and processing accuracy of GF-4 images. The experimental results show that the indexes of radiance accuracy of GF-4 PMS images, are all better than 3%, including average line standard deviation, mean standard deviation and generalized noise, and the signal-to-noise ratio of typical surface features is better than 40dB; and the internal geometric distortions in vertical orbit and along orbit directions are better than 0.8 pixel.
relative radiometric correction; geometric accuracy analysis; in-orbit geometric calibration of array camera; GF-4 satellite
TP391.41
: A
: 1009-8518(2016)04-0016-10
10.3969/j.issn.1009-8518.2016.04.003
徐文,男,1963年生,博士毕业于哈尔滨工业大学管理科学与工程专业,研究员。国家陆地观测卫星地面系统总师,主要从事遥感卫星地面系统的设计建设和国产遥感卫星数据的应用推广研究。E-mail: xuwen@spacechina.com。
(编辑:夏淑密)
2016-04-21
国家重大科技专项工程
