基于NSCT和自适应模糊阈值遥感图像去噪算法

黄 涛,薛丰昌,钱洪亮,周 明

(1.上海市嘉定区气象局，上海 201800;2.南京信息工程大学 计算机与软件学院，江苏 南京 210044;3.南京信息工程大学 遥感学院，江苏 南京 210044)

基于NSCT和自适应模糊阈值遥感图像去噪算法

黄 涛1,2,薛丰昌3,钱洪亮3,周 明1

(1.上海市嘉定区气象局，上海 201800;2.南京信息工程大学 计算机与软件学院，江苏 南京 210044;3.南京信息工程大学 遥感学院，江苏 南京 210044)

针对遥感图像去噪过程中硬阈值去噪的伪吉布斯(Gibbs)现象带来的视觉失真、软阈值去噪对图像细节造成的“过扼杀”现象以及峰值信噪比(PSNR)较低等问题，提出一种基于非下采样Contourlet变换(Non-Subsampled Contourlet Transform,NSCT)和自适应模糊阈值的遥感图像去噪算法。该算法通过对含噪图像进行NSCT变换，从而得到不同尺度与方向上的NSCT域系数，然后结合噪声的分布特点，基于贝叶斯萎缩法，对BayesShrink阈值进行了改进，并结合模糊理论，构造模糊阈值函数，实现对变化域内的系数进行处理，最后将处理后的系数进行NSCT反变换，以得到去噪后的图像。实验结果表明，该方法不仅很好地克服了硬阈值去噪的伪吉布斯现象带来的视觉失真、软阈值去噪对图像细节造成的“过扼杀”现象，而且能有效地提高峰值信噪比，保持遥感图像丰富的纹理信息。

非下采样Contourlet变换；模糊阈值；遥感图像；去噪算法

0 引 言

由于图像在其采集和传输的过程中，通常会受到噪声影响，而去除噪声的关键就是要保存图像中的重要影像特征，并有效抑制噪声。但为了得到理想的去噪效果，去噪算法就要适应图像边缘的不连续性。所以目前图像去噪已成为计算机图像处理领域中一个重要的研究课题。

近年来，小波变换得到了很大的发展，在应用到图像处理领域之后也取得了可观的成果，但由一维小波扩展成的二维小波基具有正方形的支撑区间，只能刻画图像中点的奇异性，难以刻画图像中的边缘和纹理等高维几何特性[1]。

因此，具有“各向异性”的多尺度几何分析应运而生，其中，Do和Vetterli提出的Contourlet变换(CT)是目前效果比较好的一种方法。该方法有较好的方向敏感性和各向异性，可以较为准确地将图像边缘信息捕获到不同尺度不同频率的子带中，用最少的系数来逼近奇异曲线，可以有效地实现图像多分辨率的、局部的、多方向的展开[2]。但是由于在Contourlet变换过程中采用了下采样操作，不具有平移不变性，在去噪时奇异点附近会产生伪吉布斯现象，且子带存在频谱混叠现象，从而在一定程度上削弱了Contourlet变换的多方向选择性。为了弥补这一缺点，Cunha等提出了非下采样的Contourlet变换(NSCT)[3]，该方法通过迭代非下采样滤波器组来获得平移不变、多分辨、多方向特性，更好地对图像进行稀疏表示，有效地表达图像的纹理特征。

由于遥感图像在其生成、传输、接收和记录的一系列过程中，都会受到各种大气效应与电离层辐射的影响，而产生各种各样的噪声，进而影响特征提取、信息分析和模式识别等遥感图像的进一步应用，所以图像去噪是遥感图像预处理阶段一个重要环节。由于遥感图像纹理丰富的特点，将多尺度多方向的Contourlet变换及其发展应用到遥感图像的处理中具有重大意义，其在图像去噪领域也已有若干种方法，其中比较有代表性的是CT、NSCT结合阈值去噪[4-7]及尺度相关去噪[8-9]。

文中在NSCT的基础上，对其变换域内系数的特点进行了研究，基于贝叶斯萎缩法提出了一种自适应的阈值选取方法，并将模糊集理论引入到图像去噪中，构造了一种自适应的模糊阈值函数。

实验结果表明，该方法不仅能很好地克服硬阈值去噪的伪吉布斯(Gibbs)现象带来的视觉失真、软阈值去噪对图像细节造成的“过扼杀”现象，而且能够有效地提高峰值信噪比(PSNR)，保持遥感图像丰富的纹理信息。

1 非下采样Contourlet变换简介

Contourlet变换[10]是通过Laplacian(LP)金字塔分解和方向滤波器组(DFB)相结合而实现的一种多分辨率的、局域的、多方向的图像表示方法。其变换的核心是“塔式方向滤波器组”(Pyramidal Directional Filter Bank，PDFB)，即将拉普拉斯金字塔和方向滤波器组进行组合，从而构造出的一种双迭代滤波器结构，也称Contourlet滤波器组。图1展示的是利用Contourlet滤波器组对图像进行多尺度及方向分解的流程。图像的拉普拉斯金字塔分解连续对其带通影像进行子带分解，将方向滤波器加到这些带通子带，便能有效地捕获方向信息。

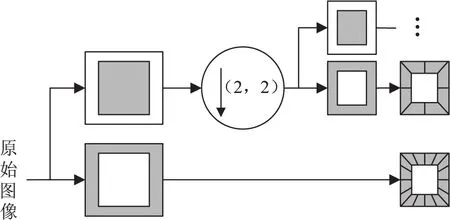
图1 用Contourlet滤波器组对影像进行分解的流程

Contourlet变换的实现过程如下[11]：

Contourlet变换首先需要对图像进行多尺度变换，以检测不同尺度下的奇异点；然后再通过一个具有局部性的方向变换将同一尺度下相邻的奇异点连接成线段结构，通过使用类似于线段的基函数去逼近原始图像，以实现对图像信号的稀疏分离。它是将尺度分析和方向分析分开进行的。首先采用拉普拉斯金字塔对图像进行多尺度分析，从而得到一系列的带通及下采样图像；接着由方向滤波器组将分布在同方向的奇异点合成为一个系数。影像的拉普拉斯金字塔分解连续地对其带通影像进行子带分解，当对这些带通子带应用方向滤波器组时，便能有效地“捕获”方向信息。

拉普拉斯金字塔和方向滤波器组都具有完全重构的特性，所以由其组合得到的塔式方向滤波器组也能实现完全重构，并且塔式方向滤波器组与拉普拉斯金字塔分解具有相同的冗余度。

这里可以用内积的形式表示Contourlet变换：

cj,d=〈sj,φd〉=〈〈x,φj〉,φd〉=〈x,〈φj,φd〉〉= 〈x,βj,d〉

(1)

式中，βj,d=〈φj,φd〉为Contourlet变换系数空间RM×N的基；x为输入信号。

为了在保留Contourlet变换的频率分割结构的同时实现平移不变性，将原Contourlet变换中对图像的下采样步骤去掉，构造相应的分级和各种方向滤波器即得到NSCT。

图2为NSCT的总体结构示意图。

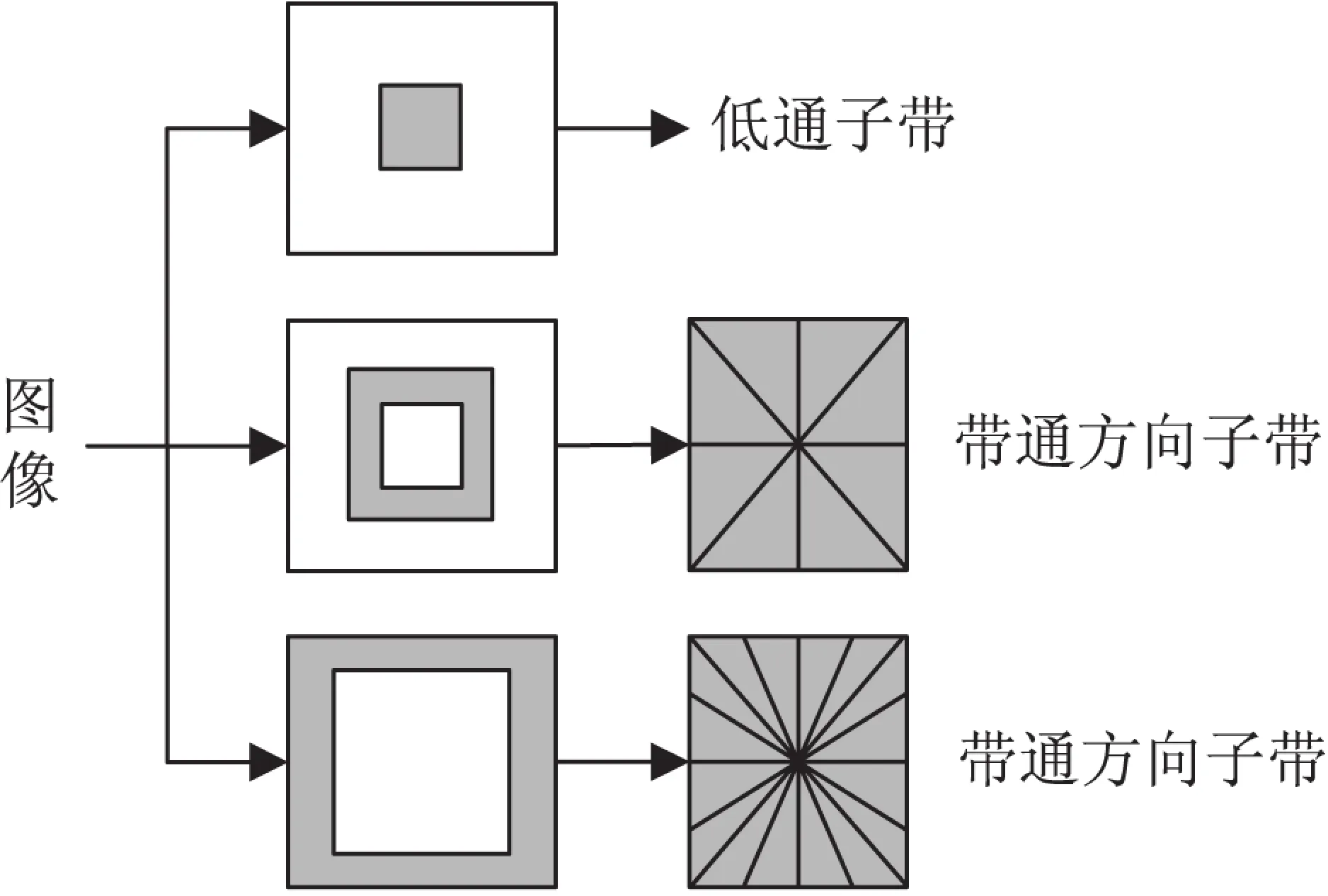
(a)实现NSCT的滤波器组结构

可以看出，NSCT主要由两个具有平移不变性的部分组成：

(1)非下采样金字塔分解，保证了变换的多尺度特性；

(2)非下采样方向滤波器组，使变换具有多方向性。

NSCT借鉴了àtrous算法的思想，不对LP分解后的分量和DFB分解后的分量进行下采样，而是对滤波器进行上采样，从而实现平移不变性[12]。它首先用非下采样塔式滤波器(Non-SubsampledPyramid,NSP)将输入图像分解为高频与低频两部分，然后用非下采样方向滤波器组(Non-SubsampledDirectionalFilterBank,NSDFB)将高频部分分解为若干方向。NSCT目前的应用主要集中在图像去噪、图像融合等领域。

2 变换域内阈值去噪原理

Contourlet变换能够抓住图像的几何结构特征，这对于处理纹理信息较为丰富的遥感图像尤为重要，并且将多尺度分析应用于图像的去噪领域已经取得了许多研究成果[13]。

在对图像进行去噪的实验中，通常假设图像被均值为0、方差为σ2的加性平稳高斯白噪声所污染，则噪声图像的模型可表示为：

(2)

含噪图像经NSCT变换后可表示为：

Wg=Wf+Wn

(3)

这里，Wg表示含噪图像的NSCT变换系数;Wf表示原图像的NSCT变换系数;Wn代表噪声的NSCT变换系数。

NSCT变换域内去噪，就是要从Wg中恢复原始图像的变换系数，并保持Wf的特征，优化均方差[14]。

NSCT变换具有去相关性质，这保证了图像经变换后的能力集中在有限的变换域系数上，其余大部分变换域系数的幅值接近于零，噪声经变换后仍是噪声，能量均匀地分布在所有的变换域系数上。根据该特性，常用的一种简单去噪方法是阈值去噪，大致可分为以下三个步骤：

(1)对含噪图像进行NSCT变换，得到图像NSCT变换域内系数；

(2)设定阈值，分别按照某种规则，对NSCT变换域内各层大于或小于阈值的系数进行处理；

(3)对处理后的系数进行NSCT逆变换重构，得到去噪后的图像。

通过近两年来的党建工作实践，形成了重担共挑的机制；强化了廉洁守纪的氛围；提升了管党治党的信心；巩固了双基建设的成果；增强了争创一流的能力；推动了党建工作和生产经营深度融合、同频共振。我们深深地体会到抓党建就是抓发展，抓发展必须抓党建，党建工作做实了就是生产力，做强了就是竞争力，做深了就是凝聚力。

变换域内阈值去噪中的两个关键环节是阈值的确定和阈值函数，其中目前主要的阈值估计方法[15-16]有统一阈值、3σ～4σ阈值和BayesShrink阈值等，常见的阈值函数主要是硬阈值函数和软阈值函数。

3 基于NSCT的自适应模糊阈值去噪

3.1 适应阈值的选取

阈值去噪是图像去噪方法中一种常见的去噪方法，而“如何选取阈值”对阈值去噪具有相当重要的影响，不同的阈值处理具有不同的效果。

在小波系数服从广义高斯分布的假设下，BayesShrink阈值能获得接近于理想阈值的去噪效果。实验证明，图像在NSCT变换域内不同尺度不同方向子带的系数也服从广义的高斯分布[17]。文中在贝叶斯萎缩法的基础上，考虑到NSCT变换域内不同尺度、不同子带系数的差异性，对其进行了改进，增加了一个改正因子。

BayesShrink阈值的表达式为：

(4)

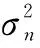
改进后的阈值公式表示为：

(5)

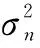
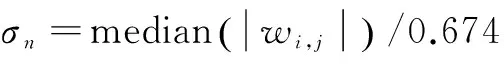
(6)

其中，wi,j为NSCT域内不同尺度不同子带的高频系数。

信号方差σf根据最大似然估计法得到，其表达式为：

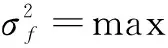
(7)

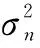
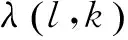
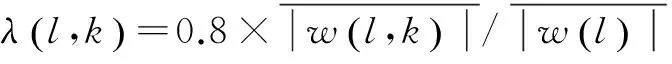
(8)

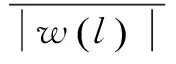
改正因子使得对于系数整体较小的子带，阈值相对小一点，以保留更多的系数；对于系数整体较大的子带，用来增大阈值来抑制更多的噪声，这样有助于提高图像的重构质量。

3.2 模糊阈值函数

在阈值函数的构造过程中，由于细节与噪声的分界并不是确定的，存在既是噪声、又不是噪声或既是边缘信息又不是边缘的问题，即具有一定的模糊性[18-20]，文中构造了一个图像细节信息的隶属函数，即

(9)

其中，a为可调节参数，可根据所需要的效果进行调节，一般在(0,1]区间上取值。

于是，根据细节信息的隶属度，可以构造得出模糊阈值函数的表达式为：

(10)

其中，隶属度越大，表示细节信息的可靠性越高，越逼近原图像，与软阈值函数比较，能更好地恢复图像中的边缘轮廓，不易造成细节信息的损失。

3.3 基于NSCT的自适应模糊阈值去噪算法

文中所采用的算法流程描述如下：

(1)读入含噪图像，对其进行NSCT变换得到含噪图像的低频近似系数及在不同尺度、不同方向上的NSCT域高频系数；

(2)分别对不同尺度不同子带内的高频系数处理得到其相应的阈值T：

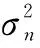
②由各方向子带的高频系数按照式(7)计算得到其相应子带图像信号的方差σf；

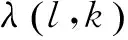
④将①～③分别得到的参数的值代入式(5)中计算得到不同尺度不同子带的阈值T。

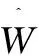
①由式(9)计算不同尺度不同子带所有系数相应的隶属度Si,j；

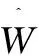
3.4 实验结果与分析

为验证文中算法的有效性，实验采用纹理较丰富的图像，截取其中大小为243*258的一部分，分别叠加了均值为0、标准方差为0.005、0.01和0.02的高斯白噪声后，用基于NSCT的软阈值方法、硬阈值方法和文中算法对其进行去噪实验，对比了各方法对含噪程度不同的图像去噪后的视觉效果及PSNR值。实验在MATLAB 7.1平台下进行。实验中，NSCT变换所采用的塔式滤波器组和方向滤波器组均分别为“9-7”和“pkva”，进行三层分解，方向数分别为4、4、8。

图3给出了所加噪声标准方差为0.01的含噪图像及各方法去噪后的效果图。

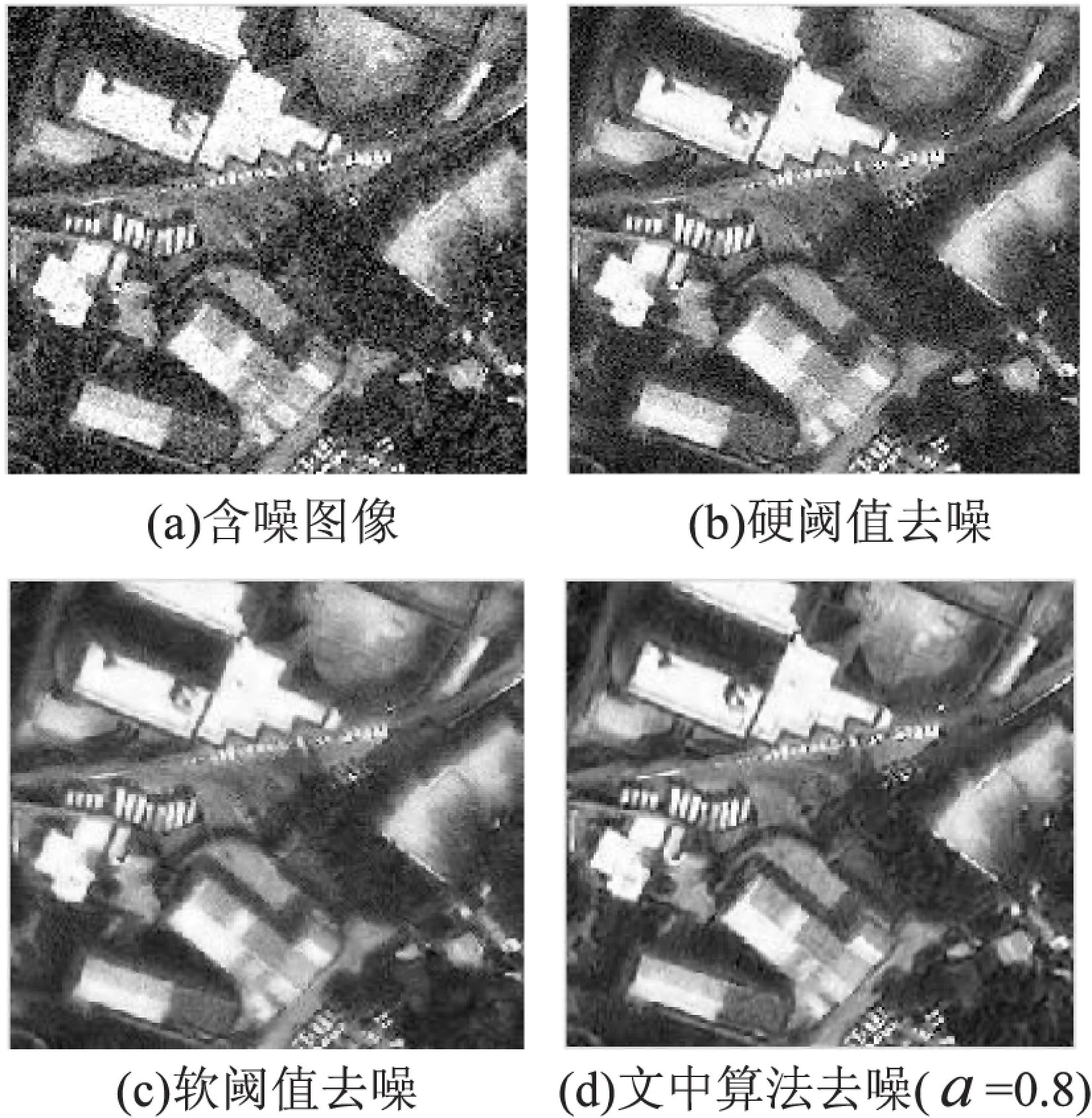
图3 噪声标准差为0.01的图像去噪结果

表1给出了几种方法对含噪程度不同图像去噪后的图像PSNR值。

从实验结果可以看出，文中算法对纹理图像的去噪效果相对较好，对于含噪声程度不同的图像其去噪能力都表现良好，优于基于NSCT的硬阈值或软阈值算法。不仅能有效地去除噪声，提高去噪图像的PSNR，而且能较好地恢复图像的细节轮廓信息，并克服了硬阈值去噪的伪吉布斯现象带来的视觉失真或者软阈值去噪对图像细节造成的“过扼杀”现象。

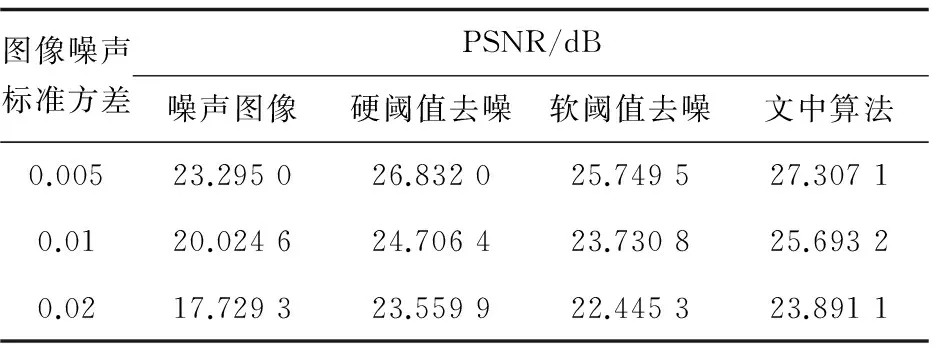
表1 含噪程度不同的图像用各方法去噪后的PSNR

在模糊阈值函数中参数a的选择上，可以根据不同的需要灵活选择以构造适应不同图像的模糊阈值函数，上述实验中选择的参数为0.8。

4 结束语

图像去噪作为图像处理的关键环节，以非下采样Contourlet变换的平移不变性、频率选择性、正则性等优良性能为基础，并结合模糊集理论，提出了一种新的遥感图像去噪方法。

首先通过对含噪图像进行NSCT变换，得到不同尺度、不同方向上的NSCT域系数；然后结合噪声分布特点对BayesShrink阈值进行改进；再结合模糊理论构造了模糊阈值函数处理变换域内的系数；最后将处理后的系数进行NSCT反变换，得到去噪后的图像。

实验结果表明，文中算法对于含噪声程度不同的图像其去噪能力均表现良好，且优于基于NSCT的硬阈值或软阈值算法。同时，通过实验发现文中算法还能够较好地恢复图像的细节轮廓信息，并克服硬阈值去噪的伪吉布斯现象或者软阈值去噪对图像细节造成的“过扼杀”现象。

[1] 齐乃新,曹立佳,杨小冈,等.基于改进邻域收缩法的非下采样Contourlet变换域红外图像去噪[J].科学技术与工程,2014,14(23):103-107.

[2]DoMN,VetterliM.Thecontourlettransform:anefficientdirectionalmultiresolutionimagerepresentation[J].IEEETransactionsonImageProcessing,2005,14(12):2091-2106.

[3]CunhaDAL,ZhouJ,DoMN.Thenonsubsampledcontourlettransform:theory,design,andapplications[J].IEEETransactionsonImageProcessing,2006,15(10):3089-3101.

[4] 徐华楠,刘 哲,胡 钢.Contourlet变换及其在图像去噪中的应用研究[J].计算机应用研究,2009,26(2):401-405.

[5] 曾业战,钱盛友,刘 畅,等.非下采样Contourlet变换自适应图像去噪方法[J].计算机工程与应用,2010,46(10):157-159.

[6] 周爱平，梁久祯．基于非下采样Contourlet变换多聚焦图像融合[J]．计算机工程与科学，2010, 32(11) 71-74．

[7] 李 勇，刘云秀．基于2DPCA-NSCT变换的多光谱与全色图像融合[J]．计算机工程与科学，2013, 35(7) 143-148．

[8] 程光权,成礼智.基于冗余Contourlet变换的图像相关法去噪[J].中国图象图形学报,2008,13(9):1678-1682.

[9]ChangSG,于YuB,VetterliM.Spatiallyadaptivewaveletthresholdingwithcontextmodelingforimagedenoising[J].IEEETransonImageProcessing,2000,9(9):1522-1531.

[10] 岳许要,杨恢先,祝 贵,等.非采样Contourlet变换与局部二值模式相结合的人脸识别[J].计算机应用,2012,32(7):1890-1893.

[11] 殷 明,刘 卫,王治成.非下采样Contourlet变换域统计模型红外图像去噪[J].光电工程,2012,39(8):46-54.

[12] 杨建慧,白 超.àtrous小波-NSCT遥感图像融合[J].计算机工程与应用，2013，49(5):170-173．

[13] 付仲凯,王向阳,郑宏亮.一种新的非下采样Contourlet域图像去噪算法[J].计算机科学,2009,36(11):286-289.

[14] 何雅丽，杨恢先，李 利，等．邻域窗能量平均的Contourlet变换自适应阈值去噪算法[J].计算机应用,2012,32(5)：1286-1288．

[15]DonohoDL.De-noisingbysoft-thresholding[J].IEEETransactionsonInformationTheory,1995,41(3):613-627.

[16]ChangSG,YuB,VetterliM.Adaptivewaveletthresholdingforimagedenoisingandcompression[J].IEEETransactionsonImageProcessing,2000,9(9):1532-1546.

[17]PoDDY,DoMN.Directionalmultiscalemodelingofimagesusingthecontourlettransform[J].IEEETransactionsonImageProcessing,2006,15(6):1610-1620.

[18]SelvathiD,MaliniC,ShanmugavalliP.AutomaticsegmentationandclassificationoflivertumorinCTimagesusingadaptivehybridtechniqueandContourletbasedELMclassifier[C]//Procof2013internationalconferenceonrecenttrendsininformationtechnology.[s.l.]:IEEE,2013:250-256.

[19] 黄宇达,魏 霞,王迤冉,等.一种基于非下采样Contourlet变换的自适应阈值去噪方法[J].计算机与数字工程,2012,40(5):111-113.

[20] 杨晓慧,焦李成,牛宏娟,等.基于多阈值的非下采样轮廓波图像去噪方法[J].计算机工程,2010,36(4):200-201.

Remote Sensing Image Denoising Algorithm Based on NSCT and Adaptive Fuzzy Threshold

HUANG Tao1,2,XUE Feng-chang3,QIAN Hong-liang3,ZHOU Ming1

(1.Jiading Meteorological Bureau of Shanghai Municipality,Shanghai 201800,China;2.School of Computer and Software,Nanjing University of Science Information and Technology,Nanjing 210044,China;3.School of Remote Sensing,Nanjing University of Science Information and Technology,Nanjing 210044,China)

In order to overcome the visual distortion caused by Gibbs phenomenon of hard thresholding,the "over strangle" phenomenon caused by processing image detail of soft thresholding,the lower PSNR and other issues in the process of image denoising,an algorithm of denoising for remote sensing images based on NSCT and adaptive fuzzy threshold was proposed.First,transform the noisy image by NSCT to get the NSCT domain coefficients of different scales and different directions.Then improve the BayesShrink threshold with the characteristics of the noise distribution based on Bayesian shrinkage method,constructing a fuzzy threshold function with fuzzy theory to process the coefficients within the changing domain.Last,inversely transform the processed coefficients by NSCT to get the denoised images.Experimental results show that the proposed algorithm can not only overcome the visual distortion caused by Gibbs phenomenon of hard thresholding,the "over strangle" phenomenon caused by processing image detail of soft thresholding well,but also improve PSNR effectively,keeping the rich texture information of remote sensing images.

NSCT;fuzzy threshold;remote sensing images;denoising algorithm

2015-04-03

2015-07-08

时间：2016-01-04

国家级城市气象科学研究基金(IUMKY&UMRF 201103)；江苏省博士后科研基金(1101024B)；南京信息工程大学科研基金(S8111133001)

黄 涛(1988-)，男，硕士研究生，研究方向为人工智能与算法研究、GIS与空间分析研究；薛丰昌，副教授，博士，博士后，研究方向为GIS与空间分析研究。

http://www.cnki.net/kcms/detail/61.1450.TP.20160104.1453.008.html

TP301.6

A

1673-629X(2016)01-0065-05

10.3969/j.issn.1673-629X.2016.01.013